§ О29. Принцип усреднения

Принцип усреднения — один из мощнейших методов теории возмущений. Суть его заключается в замене правых частей дифференциальных уравнений, содержащих "колеблющиеся" члены, усредненными "автономными" функциями, не содержащими явно времени t. Более подробно. Пусть, например, исходный процесс, описываемый дифференциальным уравнением, подвержен малым порядка ε возмущениям. Тогда в силу непрерывной зависимости решений от параметра в общем случае возмущения решений на фиксированном промежутке времени будут иметь тот же порядок малости, а именно ε. Если нас интересует поведение решений на больших, растущих с убыванием ε интервалах, то такого заключения уже сделать нельзя: к примеру на интервалах порядка 1/ε возмущения решений будут уже, как правило, конечными. Принцип усреднения предлагает рецепт, позволяющий заменить сложные возмущающие члены в уравнении более простыми (автономными) и при этом учесть основной вклад в процесс, вносимый этими возмущениями на временах порядка 1/ε.

Поясним сказанное на простейшем примере. Рассмотрим уравнение

x′ = ε(sin2t)x

(1)

как малое возмущение уравнения

x′ = 0

(2)

(ε — малый положительный параметр). Пусть φ и ψ — решения уравнений (1) и (2), удовлетворяющие начальному условию

x(0) = 1.

(3)

Нетрудно видеть, что φ и ψ близки при малых ε на любом промежутке [0, T] и таковыми не являются на промежутке вида [0, T/ε] (см. рис. 1). Точнее это сформулировано в следующих задачах.

Рис. 1.

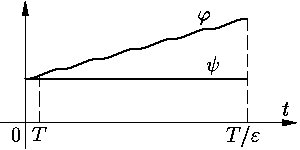
Задача О29.1. max{|φ(t) – ψ(t)|: t ∈ [0, T]} → 0 при ε → 0 для любого T > 0.

Задача О29.2. Для любого T > 0 найдется α > 0 такое, что max{|φ(t) – ψ(t)|: t ∈ [0, T/ε]} > α при всех малых ε.

Если же мы не будем отбрасывать возмущающий член ε(sin²t)x, а заменим его более простым "усредненным", а именно, заменим коэффициент sin²t в (1) его средним значением:

a = lim t→∞ 1 t ∫ t 0 sin2s ds =  1 π ∫ π 0 sin2s ds =  1 2 ,

то мы получим уравнение

x′ = 1 2 x,

(4)

решения которого аппроксимируют решения уравнения (1) уже и на промежутках длины порядка 1/ε. Точнее,

Задача О29.3. Пусть ξ — решение задачи (4), (3). Тогда max{|φ(t) – ψ(t)|: t ∈ [0, T/ε]} → 0 при любом T > 0.

Таким образом, уравнение (4) более точно, нежели уравнение (2), учитывает специфику уравнения (1). В (4) учтен "дрейф" фазовой точки под воздействием малого осциллирующего воздействия. Другими словами, принцип усреднения позволяет заменять сложное уравнение (здесь (1)) более простым автономным уравнением (здесь (4)) и при этом сохранять близость между решениями на большем по сравнению с простым отбрасыванием возмущающих членов промежутке.

Основным объектом изучения в теории принципа усреднения является уравнение вида

x′ = εf(t, x)

(5)

в котором ε — малый параметр, а f, как обычно, действует из R×Rⁿ в Rⁿ. (Мы будем предполагать, что оператор f удовлетворяет условиям теоремы Коши — Пикара и ограничен: |f(t, x)| ≤ M < ∞ при всех (t, x)). Такие уравнения с пропорциональной малому параметру правой частью называются в теории метода усреднения уравнениями в стандартной форме. К уравнениям в стандартной форме приводятся многие уравнения с параметром. Один из важнейших источников таких уравнений — теория нелинейных колебаний. Например, рассмотрим уравнение линейного осциллятора, на который действует малая возмущающая нелинейная сила εf:

x′′ + ω2x = εf(x, x′),

или, что эквивалентно, систему уравнений

x′ = y,    y′ = –ω2x + εf(x, x′).

(6)

Невозмущенное уравнение (ε = 0), очевидно, имеет двупараметрическое семейство решений x(t) = acos(ωt + φ), y(t) = x′(t) (параметрами служат амплитуда a и фаза φ). Метод переменной фазы и амплитуды заключается в том, что решение возмущенного уравнения (6) ищут в том же виде x(t) = acos(ωt + φ), y(t) = ωasin(ωt + φ), предполагая, что a и φ являются неизвестными функциями времени. Несложные преобразования показывают, что a и φ удовлетворяют системе вида

a′ = εA(a, φ, t),

φ′ = εΦ(a, φ, t)

с периодически зависящими от параметра t функциями A и Φ.

Задача О29.4. Докажите последнее утверждение.

Основным ограничением в теории принципа усреднения на уравнение (5) является требование наличия среднего значения f по t: при каждом x ∈ Rⁿ должен существовать предел

f0(x) = lim t→∞ 1 t ∫ t 0 f(s,x) ds.

(7)

Наряду с уравнением (5) рассматривают так называемое усредненное уравнение

x′ = εf0(x),

(5у)

являющееся, по сравнению с исходным, более простым — автономным. В классической механике принцип усреднения часто приводит даже к интегрируемым в квадратурах уравнениям.

Сингулярный характер зависимости уравнения (5) от параметра становится хорошо виден после замены переменных x = W(ε)y, где W(ε) представляет собой оператор растяжение функции вдоль оси t в 1/ε раз: [W(ε)y](t) = y(εt). Уравнения (5) и (5у) переходят (докажите!), соответственно в уравнения

y′ = f ( t ε , y ) ,

(8)

y′ = f0(y).

(8у)

Будем рассматривать для уравнений (5), (5у) и (8), (8у) задачу Коши определяемую начальным условием

x(0) = x0

(9)

и, соответственно, — условием

y(0) = x0.

(10)

Задача О29.5. Покажите, что если φ_ε — решение задачи Коши (5), (9) на отрезке [0, T/ε], то функция ψ_ε = W(ε^–1)φ_ε — решение задачи Коши (8), (10) на отрезке [0, T] и наоборот. Докажите аналогичное утверждение для задач (5у), (9) и (8у), (10).

Предположим усредненная задача Коши (8у), (10) имеет при ε = 1 на отрезке [0, T] единственное решение ξ₁. (На самом деле требование существования и единственности решения ξ₁ в нашей ситуации излишне, т. к. f₀ одновременно с f удовлетворяет условию Липшица (докажите!)). Тогда, очевидно, задача Коши (5у), (10) имеет на отрезке [0, T/ε] единственное решение ξ_ε = W(ε)ξ₁. Обозначим через φ_ε (единственное) решение задачи Коши (5), (9). Очевидно, функция ψ_ε = W(ε^–1)φ_ε — решение задачи (8), (10).

Задача О29.6. Покажите, что если max{|ψ_ε(t) – ξ₁(t)|: t ∈ [0, T]} → 0, то max{|φ_ε(t) – ξ_ε(t)|: t ∈ [0, T/ε]} → 0.

Функция ψ_ε, очевидно, удовлетворяет интегральному уравнению

y(t) = x0 + ∫ t 0 f [ s ε , y(s) ] ds,   t ∈ [0, T],

(11)

а ξ₁ — интегральному уравнению

y(t) = x0 + ∫ t 0 f0[y(s)] ds, t ∈ [0, T],

(11у)

Интуитивно ясно, что интегралы в правых частях этих уравнений в каком-то смысле близки. Действительно, если во всяком случае, в (11) и (11у) y — функция-константа, то

lim ε→0 ∫ t 0 f ( s ε , y ) ds  = lim ε→0 ∫ t 0 f ( s ε , y ) d ( s ε ) =   lim ε→0 t ε t ∫ t/ε 0 f(ρ, y) dρ =

= t · lim τ→∞ 1 τ ∫ τ 0 f(ρ, y) dρ = t · f0(y) = ∫ t 0 f0(y) ds.

Оказывается равенство

lim ε→0 ∫ t 0 f [ s ε , y(s) ] ds = ∫ t 0 f0[y(s)] ds

(12)

справедливо и для любой непрерывной функции y. План доказательства этого утверждения изложен в следующих задачах.

Задача О29.7. Покажите, что

lim ε→0 ∫ t2 t1 f ( s ε , y ) ds= ∫ t2 t1 f0(y) ds.

при любых t₂ ≥ t₁ ≥ 0 и y ∈ Rⁿ.

Задача О29.8. Покажите, что (12) справедливо для любой ступенчатой функции.

Задача О29.9. Аппроксимируя функцию y ступенчатыми, докажите справедливость (12) для любой непрерывной функции y.

Более того, если {y_k} — равномерно на [0, T] сходящаяся к функции y₀ последовательность непрерывных функций и ε_k → 0, то

lim k→∞ ∫ t 0 f [ s εk , yk(s) ] ds = ∫ t 0 f0[y0(s)] ds.

(13)

Задача О29.10. Докажите (13).

Центральный результат теории принципа усреднения —

Теорема Н.Н. Боголюбова.

max{|φε(t) – ξε(t)|: t ∈ [0, T/ε]} → 0 при ε →0.

Схема ее  д о к а з а т е л ь с т в а  близка к схеме доказательства теоремы о непрерывной зависимости решений от параметра. В силу утверждения задачи О29.6 достаточно показать, что

max{|ψε(t) – ξ1(t)|: t ∈ [0, T]} → 0 при ε → 0.

(14)

Хотя правая часть уравнения (8) не является непрерывной по параметру ε в точке ε = 0, интеграл от нее уже непрерывен по этому параметру: пределом при ε → 0 в этом "интегральном" смысле служит функция f₀ (такой характер зависимости от параметра называют иногда интегральной непрерывностью). Это и позволяет провести стандартные рассуждения. А именно, если (14) не выполнено, то для некоторых δ > 0, последовательности ε_k → 0 и последовательности {t_k} ⊂ [0, T]

|ψεk(tk) – ξ0(tk)| > δ.

(15)

Из уравнения (8) следует, что

|ψε′(t)| ≤ M,    |ψε(t)| ≤ |x0| + MT,    t ∈ [0, T].

Последнее означает равномерную ограниченность и равностепенную непрерывность множества {ψε}, что позволяет без ограничения общности считать последовательность {ψεk} равномерно сходящейся к некоторой непрерывной функции ψ1 (для доказательства этого нужно воспользоваться теоремой Арцеля — Асколи). Переходя теперь с помощью (13) в равенстве

ψεk(t) = x0 + ∫ t 0 f [ s εk , ψεk(s) ] ds,   t ∈ [0, T]

к пределу при k → ∞, получим равенство

ψ1(t) = x0 + ∫ t 0 f[ψ1(s)]ds,    t ∈ [0, T]

означающее, что ψ₁ является решением задачи (8у), (10) при ε = 1. Остается заметить, что ψ₁ ≠ ξ₁ (в (14) последовательность {t_k} можно считать, не ограничивая общности, сходящейся к некоторому t₀ ∈ [0, T] и тогда в пределе |ψ₁(t₀) – ξ₁(t₀)| > δ), а это противоречит единственности решения задачи (8у), (10). Теорема доказана.

Метод усреднения оказывается эффективным и в задаче о периодических и почти периодических колебаниях. Если предполагать, например функцию f в уравнении (5) периодической по t: f(t + T, x) ≡ f(t, x), то условие существования среднего значения f₀ выполняется автоматически:

f0(x) = 1 T ∫ T 0 f(s, x) ds.

Задача О29.11. Докажите последнее равенство.

Оказывается в этом случае в окрестности асимптотически устойчивой особой точки усредненного уравнения существует периодическое решение неусредненного уравнения. Точнее, имеет место

Вторая теорема Н.Н. Боголюбова. Если x* — асимптотически устойчивая особая точка уравнения (5у), то при малых ε > 0 уравнение (5) имеет асимптотически устойчивое T-периодическое решение φ_ε такое, что max{|φ_ε(t) – x*|: t ∈ R} → 0.

Ее доказательство выходит за рамки книги.

В заключение продемонстрируем возможности принципа усреднения в получении асимптотических разложений по малому параметру. Рассмотрим уравнение

x′ = εf1(t, x) + ε2f2(t, x) + ... + εN fN(t, x) + εN+1 fN+1(t, x).

(16)

Специальной заменой переменных вида

x = y + εq1(t, x) + ... + εN qN(t, x)

(17)

(она называется заменой Боголюбова — Крылова) уравнение (16) может быть приведено к виду

y′ = εg1(y) + ε2g2(y) + ... + εN gN(y) + εN+1 gN+1(t, y)

(18)

(и таким образом, вся "неавтономность" уравнения остается в самом младшем члене). При этом функции qi и gi выписываются в явном виде. Если теперь функция gN+1 имеет среднее значение g0N+1, то рассматривают (автономное) усредненное уравнение

y′ = εg1(y) + ε2g2(y) + ... + εNgN(y) + εN+1 g0N+1(y).

(19)

Пусть теперь φ_ε — решение задачи (16), (9). Асимптотическим приближением решения φ_ε называется полученная по формуле (17) функция x_ε, в которой y — решение задачи (19), (10). Оказывается x_ε является асимптотическим разложением решения φ_ε на отрезке [0, T/ε] в том смысле, что

max{|φε(t) – xε(t)|: t ∈ [0, T/ε]} = o(εN).

Литературные указания. Хотя идеи принципа усреднения восходят, по-видимому, еще к Ньютону, который исследуя движения маятника при наличии сопротивления, получил формулу для решения, совпадающую с формулой, получаемой методом усреднения, современные черты теория принципа усреднения приобрела в XX веке, в основном, в работах Н.М. Крылова и Н.Н. Боголюбова [Крылов — Боголюбов, Крылов — Боголюбов]. Современное изложение теории можно найти в монографиях [Боголюбов — Митропольский, Волосов — Моргунов, Митропольский, Митропольский, Митропольский — Лыкова, Хейл].

Задачи. О29.12. Покажите, что уравнение

x′ = Ax + εf(t, x),

в котором A — n×n-матрица, а f: R×Rⁿ →Rⁿ заменой переменных x = e^Aty приводится к стандартной форме.

О29.13. Покажите, что уравнение с быстро колеблющейся правой частью

x(n) = f(ωt, x, x′, ..., x(n – 1)),

где ω — большой параметр, заменой переменных t = τ/ω, x′ = x₁, ..., x^(n–1) = x_n–1 приводится к стандартной форме.

О29.14. Покажите, что система

x′ = εf(t, x, y),    y′ = ω + εg(t,x, y)

заменой переменных x = ξ, y = η + ωt приводится к стандартной форме.

О29.15. Методом усреднения найдите приближенное решение задачи Коши для системы уравнений

x′ = ε(α + βsin y),    y′ = ω + ε(cos t)x.

О29.16. Методом переменной фазы и амплитуды приведите к стандартной форме уравнение Ван дер Поля

x′′ – ε(1 – x2)x′ + x = 0

(ε — малый положительный параметр). Постройте соответствующее усредненное уравнение. Найдите приближенное решение задачи Коши для уравнения Ван дер Поля.

О29.17. Покажите, что если δ(ε)/ε →0 при ε → 0, то

max{|φ(t) – ξ(t)|: t ∈ [0, T/δ(ε)]} → ∞ при ε → 0,

где φ и ξ — решения задач (1), (3) и (4), (3), соответственно. Таким образом, вообще говоря, близости решений неусредненного и усредненного уравнений на промежутках длины порядка большего, чем 1/ε нет.

О29.18. В то же время, если φ и ξ — решения задач Коши

{ x′ = –ε(sin2t)x, x(0) = 1   и   { x′ = –  ε 2  x,   x(0) = 1,

то max{|φ(t) – ξ(t)|: t ∈ [0, ∞)} → 0 при ε → 0. Докажите! Причина отличия от предыдущей задачи заключается в экспоненциальной устойчивости решений усредненного уравнения.

О29.19. Докажите, что если f(t, x) является тригонометрическим полиномом:

f(t, x) = k ∑ i = 1 [gi(x)cos λit + hi(x)sin λit],

то f имеет среднее значение. Найдите его.

О29.20. Докажите, что если f(t, x) представима в виде сходящегося равномерно по t при каждом фиксированном x ряда

f(t, x) = ∞ ∑ i = 1 [gi(x)cos λit + hi(x)sin λit],

то f имеет среднее значение. Найдите его.

О29.21. Пусть скалярная непрерывная функция a имеет среднее значение a0 = limt→∞1/t ∫ 0ta(s) ds. Докажите, что решения уравнений

x′ = a ( t ε ) x  и  x′ = a0x

имеют одинаковые характеристические показатели.

О29.22. Обобщите утверждение предыдущей задачи на системы линейных уравнений с периодической n×n-матрицей a.

О29.23. Пусть f, g: R×R → R — удовлетворяющие условию Липшица ограниченные T-периодические по второму аргументу функции и

f0(x) = 1 T ∫ T 0 f(s, x) ds, g0(x) = 1 T ∫ T 0 g(s, x) ds.

Докажите, что решения задачи Коши, отвечающих одним и тем же начальным условиям, для систем

{ x′ = εf(x, y), y′ = ω + εg(x,   и   { x′ = εf0(x), y′ = ω + εg(x)

близки при малых ε на промежутках длины порядка 1/ε.

File based on translation from T_EX by T_TH, version 2.32.
Created 22 Mar 2000, 21:12.
Last modified 2 May 2002.