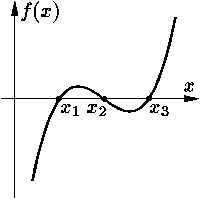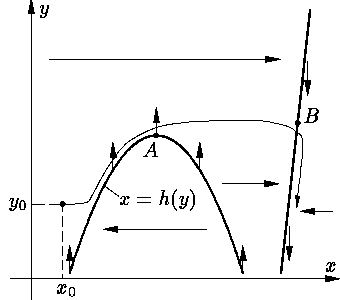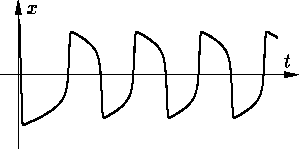|
§ О28. Дифференциальные уравнения с малым параметром при старшей производной |

|
Не было гвоздя —
Подкова
Пропала.
Не было подковы —
Лошадь
Захромала.
Лошадь захромала —
Командир
Убит.
Конница разбита —
Армия
Бежит.
Враг вступает в город,
Пленных не щадя,
Оттого, что в кузнице
Не было гвоздя.
Английская песенка
Совершенно иной (по сравнению с описанным в
§ 4.1)
характер приобретает зависимость от параметра решений обыкновенных
дифференциальных уравнений в случае, если малый параметр входит в
уравнение множителем при старшей производной. Такие уравнения,
называемые обычно сингулярно возмущенными
уравнениями (объяснение термина см. ниже),
возникают во многих разделах естествознания: в электро- и
радиотехнике, механике, гидро- и аэродинамике и т. д. Например,
колебания маятника малой
массы ε описывает дифференциальное уравнение
|
εx′′ +
ax′ + b·sin x =
0. |
Мы рассмотрим сначала простейший класс уравнений с малым параметром
при старшей производной, а именно, уравнения вида
в котором f: R →R —
непрерывно дифференцируемая функция, а ε —
малый положительный параметр. Для уравнения (1)
рассмотрим задачу Коши,
определяемую начальным условием
Нас интересует поведение решений задачи
(1) – (2) при
ε → 0.
Правая часть уравнения (1) в
нормальной форме, т. е.
уравнения x′ =
ε–1f(x)
принципиально не может непрерывно зависеть от параметра ε.
Поэтому такие уравнения и называют сингулярно-возмущенными в отличие от
регулярно возмущенных уравнений, рассмотренных в
§ 4.1, правая часть которых
непрерывна по параметру.
Уравнение (1) при ε =
0 понижает порядок — становится в нашей
ситуации дифференциальным уравнением нулевого порядка (т. е.
функциональным):
Поэтому, в частности, решение уравнения (3)
(имеется в виду решение обыкновенного
дифференциального уравнения нулевого
порядка, т. е.
функция независимого аргумента t)
не может удовлетворять произвольному начальному
условию (2). Уравнение (3)
(рассматриваемое как алгебраическое) в общем случае имеет
конечное (возможно нулевое) число решений.
Наша задача — выяснить можно ли, исходя из
наличия информации о решениях уравнения (3),
получить информацию о поведении решений задачи
(1) – (2) при
ε → 0.
Рассмотрим для прояснения ситуации случай, когда уравнение
(3) имеет, например, три корня
(см. рис. 1).
Поле
направлений уравнения (1), т. е. уравнения
x′ = ε–1f(x),
при достаточно малых ε > 0
устроено, как легко видеть, так:
вне малых окрестностей нулей функции f оно почти вертикально,
причем в полосе {(t, x):
x1 < x
< x3} оно направлено "к прямой x =
x2" (см. рис. 2а).
Интегральные
кривые уравнения (1) изображены на
рис. 2б). На этом рисунке видно, что к решениям
x(t) ≡ x1 и
x(t) ≡ x3
уравнения (3) не стремятся при
ε → 0 никакие решения задачи
(1) – (2) (за исключением,
разумеется, самих этих решений). В то же время, к решению
x(t) ≡ x2
уравнения (3) стремятся при
ε → 0 решения задачи
(1) – (2),
отвечающие начальному значению x0, лежащему в
интервале (x1, x2). Решение
x(t) ≡ x2
называется устойчивым решением вырожденного
(функционального) уравнения (3)
(или говорят об устойчивом корне x2
алгебраического уравнения (3)). Оно характеризуется
условием f′(x0) < 0.
Интервал (x1, x3),
границами которого являются ближайшие к устойчивому корню x2 корни
уравнения (3), называется
областью притяжения (или влияния)
устойчивого решения x2 уравнения (3).
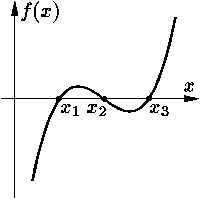
Рис. 1.
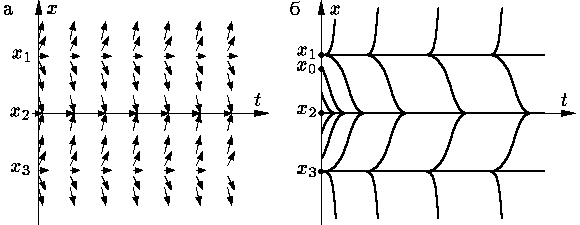
Рис. 2.
Наши наблюдения резюмирует следующая
Теорема о сингулярно возмущенном
уравнении. Пусть x(t) ≡ φ —
устойчивое решение уравнения (3),
а x0 лежит в области притяжения
корня φ. Тогда
|
|xε(t) –
φ| → 0 при всех t > 0;
| (4) |
здесь xε — решение задачи
(1) – (2).
Задача О28.1. Выписав явный вид решения, докажите
утверждение теоремы для уравнения
εx′ =
x2 – 1.
Теорема о сингулярно возмущенном уравнении доказывается
достаточно просто. Поскольку вне δ-окрестностей
нулей функции f (δ —
сколь угодно малое положительное число)
|f(x)| ≥
M(δ) > 0, вне этих окрестностей
фазовая скорость имеет порядок ε–1.
Поэтому за время порядка ε фазовая точка попадает в
δ-окрестность
Vδ устойчивого решения
φ уравнения (3). Легко показывается, что,
попав в Vδ,
фазовая точка уже ее (окрестность
Vδ)
не покинет. Утверждение теоремы следует теперь из
произвольности δ.
Задача О28.2. Восстановите детали доказательства.
Подчеркнем, что если в регулярном
случае решение зависит от параметра
равномерно по t на каждом конечном промежутке — в наших обозначениях
|xε(t) –
φ| → 0 равномерно по
t ∈ [0, T] (см. п. 4.1.3), то в сингулярном
случае это не так. Предельное соотношение (4)
принципиально не равномерно по t ∈
[0, T] (разумеется, если x0
≠ φ).
Задача О28.3. Докажите последнее утверждение.
В окрестности начального момента времени решение возмущенного
уравнения сильно отличается от решения вырожденного (при
ε = 0) уравнения. В этой окрестности
решение меняется очень быстро (скорость изменения решения имеет
порядок ε–1). Эта окрестность носит
название пограничного слоя. Наличие пограничного
слоя — характерная особенность сингулярно
возмущенных уравнений. Явление пограничного слоя широко распространено в
природе. Например, именно пограничный слой виноват в невозможности сдуть
мелкую пыль с полированного стола.
Задача О28.4. Докажите, что при любых Т >
τ > 0 предельное соотношение
(4) является равномерным по t
∈ [τ, T].
Уравнения второго и более высокого порядков с малым параметром при
старшей производной, как легко видеть, приводятся к системам вида
|
εx′ =
f(t, x, y),
y′ =
g(t, x, y), |
обычно называемым системами уравнений с малым
параметром при части производных или сингулярно возмущенными
системами; первое уравнение при этом называют уравнение
быстрых движений, а второе —
уравнением медленных движений.
Мы рассмотрим геометрически более наглядный
автономный
случай, т. е. систему
предполагая, что f, g: R2
→ R — непрерывно дифференцируемые
функции с равномерно ограниченными частными производными. Это
гарантирует однозначную
разрешимость задачи Коши для системы
(5) – (6),
задаваемой начальными условиями
При ε = 0 порядок
системы (5) – (6)
по x понижается на единицу:
(эту систему в теории сингулярно возмущенных уравнений называют
обычно вырожденной). Систему
(8) – (9) можно
трактовать как одно дифференциальное
уравнение на многообразии Γ решений уравнения
F(x, y) = 0. Потеря порядка приводит к необходимости
отказа от одного из начальных условий. Поэтому для вырожденной
системы рассматривается обычно задача Коши, выделяемая условиями
|
Векторное поле
(ε–1f(x, y),
g(x, y)) системы (5) –
(6) устроено так
(см. рис. 3а). Вне малой окрестности
многообразия Γ решений уравнения (8)
(изображенного на рис. 3а жирной линией), в которой
|f(x, y)| << ε,
векторы поля почти горизонтальны. На самóм
же Γ векторы поля вертикальны. Анализ поля
направлений показывает, что при малых ε
в начальный момент времени фазовая точка системы
(5) – (6) очень быстро
(подчиняясь, по существу, только уравнению быстрых движений
(5)) попадает в окрестность той
устойчивой кривой многообразия
Γ, в области влияния
которой находятся начальные данные (x0,
y0). Здесь пока неясно, что означают выделенные курсивом
слова; мы определим их чуть позже. Затем фазовая точка движется вдоль
устойчивого участка этой кривой (см. рис. 3б).
Устойчивый участок многообразия Γ
выделяется условием f ′x(x, y)<
0 (ср. с условием
f ′(x) < 0
в предыдущей теореме). Область же
влияния устойчивого участка многообразия
Γ — это область влияния
корня x1 (см. рис. 3б)
уравнения f(x, y) = 0 в описанном выше смысле.
|
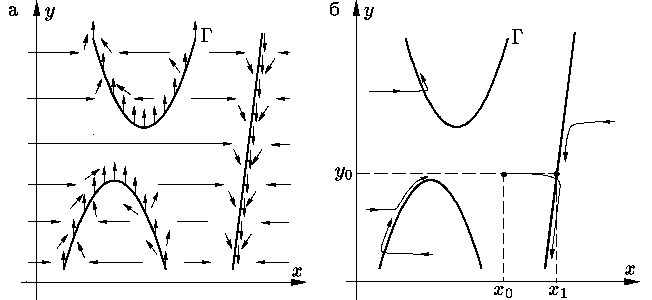
Рис. 3.
После попадания фазовой точки системы
(5) – (6) в малую окрестность
многообразия Γ она движется приблизительно
как фазовая точка вырожденной системы
(8) – (9). Движение последней
описывается следующим образом. Обозначим через h(y)
именно то решение уравнения f(x, y) = 0, которое
отвечает выбранному выше участку многообразия Γ.
Другими словами, выразим из уравнения (8) x через y,
причем из возможно нескольких решений этого уравнения выберем одно (именно его мы и
обозначили через h(y)) так, чтобы точка
(h(y), y) лежала на устойчивом участке
многообразия Γ, в области притяжения
которого находится точка (x0, y0).
Подставляя x = h(y) в уравнение
(5), получим уравнение
описывающее изменение координаты y решения системы
(8) – (9).
Пусть ψ(t) — определенное на [0, T]
решение задачи (11), (10), а
φ(t) = h[ψ(t)].
Предположим, что точка (φ(t),
ψ(t))
лежит на устойчивом участке многообразия Γ, т. е.
fx′[φ(t),
ψ(t)] < 0 при всех
t ∈ [0, T]. Тогда оказывается
(φ(t), ψ(t))
есть как раз то решение задачи Коши
(8) – (10),
к которому стремятся при ε → 0
решения сингулярно возмущенной задачи Коши
(5) – (7).
Это фундаментальное утверждение теории сингулярно
возмущенных уравнений более точно формулируется так.
Теорема А.Н. Тихонова.
Пусть (xε(t),
yε(t)) —
определенное на [0, T]
решение задачи Коши (5) –
(7). Тогда
|
|xε(t) –
φ(t)| → 0
при ε → 0 для всех t
∈ (0, T], |
|
|yε(t) –
ψ(t)| →
при ε → 0 для всех t
∈ [0, T]. |
Она представляет собой обобщение первой
теоремы данного очерка, если считать, что уравнение (1)
записано в виде сингулярно возмущенной системы
εx′ =
f(x), t′ = 1.
Задача О28.5. Докажите, что из
теоремы Тихонова вытекает теорема о сингулярно
возмущенном уравнении.
Этапы доказательства теоремы Тихонова описаны в задачах
О28.16 — О28.22 в конце очерка.
Подчеркнем, что в окрестности начального момента для x-компоненты
решения задачи (5) – (6)
имеет место пограничный слой, в то время как
y-компонента стремится к y-компоненте решения вырожденной
задачи равномерно на [0, T].
Теорема Тихонова перестает работать, в
частности, в окрестности границы области определения непрерывной
устойчивой ветви h(y) решений
уравнения (8) (точка A
на рис. 4). Здесь медленное движение фазовой
точки опять может смениться быстрым (участок AB)
и она (фазовая точка) с почти бесконечной скоростью перемещается в
окрестность другой устойчивой ветви решений вырожденного уравнения
(8) или уходит в бесконечность, если таковой нет.
Точка A называется точкой срыва,
а точка B — точкой падения.
Участок быстрого изменения решения между точкой срыва и точкой падения обычно
называют внутренним слоем. Явление срыва решения,
по существу, представляет собой бифуркацию
состояния равновесия системы (8) –
(9), если считать в ней y
медленно меняющимся параметром.
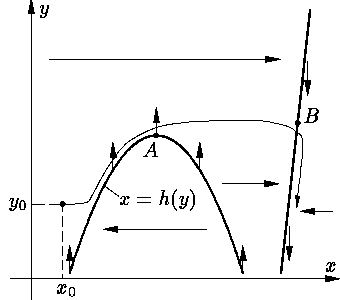
Рис. 4.
Особенно интересен случай, когда Γ
имеет вид кубической параболы (см. рис. 5а).
Похожее поле скоростей имеет, например, уравнение Ван дер Поля
| εx′′ =
x′ – | 1
3 |
(x′)3
– x. |
|
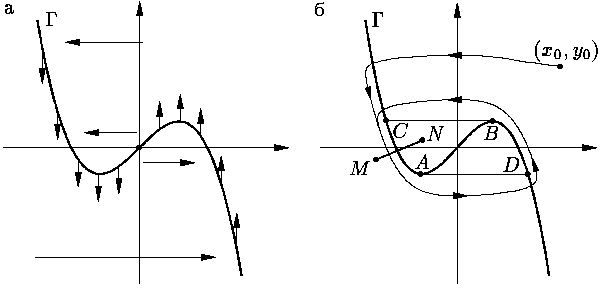
Рис. 5.
Можно доказать, что траектории соответствующей сингулярно
возмущенной системы ведут себя так (см. рис. 5б).
Начиная с произвольной точки (x0, y0),
фазовая точка быстро входит в окрестность устойчивой
ветви многообразия Γ (скажем, для
определенности, CD). Затем, медленно двигаясь вдоль этой
ветви, она попадает в окрестность точки
срыва D. Далее, подчиняясь уравнению
быстрых движений, быстро переходит в окрестность
точки падения A,
затем — медленно — в окрестность точки срыва B
и т. д., "наматываясь" на некоторый
предельный цикл
(см. рис. 5б).
Доказать это утверждение можно, например так. Определим на некотором
отрезке MN трансверсальном к кривой AB
(см. рис. 5б)
отображение последования.
Показать, что при достаточно малых ε
оно отображает этот отрезок в себя (последнее доказывается
достаточно сложно — нужно провести
аккуратные оценки решения). Поскольку отображение последования непрерывно,
оно имеет неподвижную точку, которая и порождает данный предельный цикл.
Периодическое решение, отвечающее вышеописанному
предельному циклу,
характеризуется чередованием участков быстрого и медленного его
изменения (см. рис. 6). Автоколебания такого
типа называются релаксационными
колебаниями. Они широко распространены (особенно в радиотехнике).
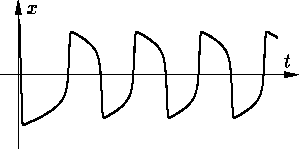
Рис. 6.
В заключение отметим, что при исследовании сингулярно возмущенных
систем обыкновенных дифференциальных уравнений весьма эффективными
оказываются асимптотические методы.
Литературные указания. Вводный материал по излагаемому
вопросу можно найти в учебнике
[Тихонов —
Васильева — Свешников]. Современное
состояние вопроса описано, напр., в монографиях
[Боголюбов —
Митропольский,
Васильева —
Бутузов, Ломов,
Митропольский,
Мищенко —
Розов, Стокер]. Изложение в
указанных книгах тесно связано с материалами следующего очерка.
Задачи.
О28.6. Пусть непрерывная функция f: R →
R не имеет нулей. Докажите, что любое решение задачи
Коши (1) – (2) в
любой точке t ≠ 0
стремится к бесконечности при ε → 0.
О28.7. Нулевой корень функции f(x) = –
x3 не является
устойчивым. Покажите, что тем не менее для
этой функции f имеет место заключение теоремы
о сингулярно возмущенном уравнении.
О28.8. Докажите, что заключение теоремы о
сингулярно возмущенном уравнении сохраняется, если заменить в ней
условие устойчивости f′(φ)
< 0 условием f(x)(x –
φ) < 0 при всех x достаточно близких
к φ.
О28.9. Докажите, что в условиях теоремы о сингулярно возмущенном
уравнении решение xε
стремится к решению φ вырожденного уравнения
с экспоненциальной скоростью порядка ε–1,
точнее, найдутся C, γ > 0 такие, что
|
|xε(t) –
φ| ≤ Ce –
γt/ε
при всех t > 0. |
О28.10. Пусть все
собственные значения матрицы A
имеют отрицательную вещественную часть. Покажите, что решение задачи Коши
стремится к нулю при ε → 0 для
каждого t > 0. Более того, это предельное соотношение равномерно по
t ∈ [τ,
∞) (τ > 0).
О28.11. Пусть A такая же, как и в
задаче О28.10. Обозначим через
xε решение задачи Коши
|
εx′ =
Ax + b(t),
x(0) = x0; |
в ней b: R
→Rn — непрерывная
функция. Пусть φ(t) =
A–1b(t).
Докажите, что при любом τ > 0
sup
t∈[τ, ∞) |
||xε(t) –
φ(t)|| → 0 при
ε → 0. |
|
О28.12. Докажите утверждения задач
О28.10 и О28.11 для задачи Коши
|
εx′ =
A(t)x + b(t), x(0) =
x0, |
в случае, когда n×n-матрица-функция
A(t) такова, что нулевое решение системы
x′ = A(t)x
асимптотически устойчиво.
О28.13. Докажите, что утверждение задачи
О28.10 не верно, если хотя бы одно
собственное
значение матрицы A имеет неотрицательную вещественную часть.
О28.14. Пусть матрица A имеет ровно k
собственных значений с отрицательной вещественной частью. Докажите, что
в Rn существует k-мерное
подпространство L, что утверждение задачи О28.10 имеет место при всех
x0 ∈ L и не имеет места
при всех x0 ∉ L.
О28.15. Пусть xε — решение задачи Коши
|
εx′′ +
ax′ + bx = 0, x(0) =
x0, x′(0) =
x1, |
а φ — решение
вырожденной задачи Коши:
φ(t) =
x0e – bt/a.
Докажите, что если a > 0, то
|
|xε(t) –
φ(t)| → 0 при
ε → 0 для всех t ∈
[0, ∞) |
и
|
|x′ε(t)
– φ′(t)|
→ 0 при ε → 0 для всех t
∈ (0, ∞), |
а если a < 0, то
|
|xε(t) –
φ(t)| → 0 при
ε → 0 для всех t ∈
(–∞, 0] |
и
|
|x′ε(t)
– φ′(t)|
→ 0 при ε → 0 для всех
t ∈ (–∞, 0).
|
В следующих семи задачах излагается план доказательства
теоремы Тихонова. В них δ
— сколь угодно малое положительное число (не одно и то же в разных задачах).
О28.16. Докажите, что замена переменных
x = W(ε)u,
y = W(ε)v,
где [W(ε)u](t) =
u(ε–1t),
переводят задачи Коши (5) –
(7) и (8) –
(10) в задачи Коши
| { |
u′ = f(u,
v),
v′ =
εg(u, v),
u(0) = x0, v(0) = y0 |
и |
{ |
u′ = f(u, v),
v′ = 0,
v(0) = y0, |
|
|
соответственно.
Добавим ко второй системе начальное условие u(0) =
x0 и обозначим решения этих систем через
(uε,
vε) и
(u0, v0).
О28.17. Покажите, что |u0(t) –
φ(t)| < δ при некотором
t0 = t0(δ)
(воспользуйтесь теоремой о сингулярно возмущенном
уравнении).
О28.18. Покажите, что
|uε(t) –
u0(t)| < δ и
|vε(t) –
v0(t)| < δ
при всех достаточно малых ε > 0
(воспользуйтесь п. 4.1.3).
О28.19. Покажите, что при достаточно малых
ε > 0
|
|xε(εt0)
– h[yε(εt0)]|
< δ |
О28.20. Определим функцию V равенством
V(x, y) =
[x – h(y)]2.
Докажите, что при t ∈
[εt0, T]
производная V в
силу системы (5) – (6)
отрицательна в δ-окрестности кривой
{(φ(t), ψ(t)):
t > 0}.
О28.21. Докажите, что
|xε(t0) –
h[yε(t0)]| <
δ при всех t ∈
[εt0, T] и малых
ε > 0.
О28.22. Докажите теорему Тихонова.