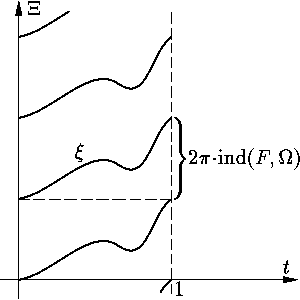|
§ О32. Топологические методы в теории дифференциальных уравнений |

|
Соединя наши познания и капиталы, мы можем действовать несравненно успешней чем порознь.
Н.В. Гоголь. Игроки
Одним из наиболее эффективных приложений топологии в теории
обыкновенных дифференциальных уравнений является применение
теории
индекса неподвижных точек непрерывных отображений. Здесь мы опишем
простейшие результаты, иллюстрирующие лишь некоторые возможности
теории индекса. Начнем с основных понятий теории индекса.
Индекс неподвижных точек — это
целочисленная характеристика произвольного заданного заданного на
замыкании Ω ограниченной области
Ω ⊂
Rn непрерывного отображения F
со значениями в Rn, не имеющего на границе
∂Ω области Ω
неподвижных точек, т. е. таких точек
x ∈ ∂Ω, что
F(x) = x.
Конструктивное определение индекса требует довольно развитой техники и для
наших целей это знание просто не нужно. Нам важно знать какими свойствами
обладает эта характеристика (тем более, что первыми тремя из
перечисляемых ниже свойств она определяется однозначно и поэтому можно
считать, что она задается аксиоматически этими свойствами ).
Два отображения F0, F1:
Ω →
Rn называются гомотопными,
если существует такое непрерывное отображение
(гомотопия) Φ:
[0,1]×Ω →
Rn,
что, во-первых, Φ(λ,
·) не имеет неподвижных точек на
∂Ω при всех
λ ∈ [0, 1], т. е.
Φ(λ, x)
≠ x
при всех λ ∈ [0, 1]
и x ∈ ∂Ω, и, во-вторых,
Φ(0, x) ≡
F0(x), а
Φ(1, x) ≡
F1(x).
Другими словами, гомотопность F0
и F1 означает, что их можно непрерывным образом
деформировать друг в друга, причем при деформации неподвижные точки
на границе не появляются. Отображение F называется
невырожденным на
Ω1, если оно не имеет на
Ω1 неподвижных точек.
Индексом неподвижных точек
(в дальнейшем — просто индекс)
непрерывного невырожденного на ∂Ω отображения
F: Ω →
Rn
называется целое число ind (F, Ω),
обладающее следующими тремя свойствами:
1º.
Если F0 и F1 —
гомотопные отображения, то
ind (F0, Ω) =
ind (F1, Ω).
|
2º. Если
Ωi (i = 1,2, ...) —
попарно не пересекающиеся открытые подмножества Ω,
а F — невырождено на
Ω \
∪∞i=1Ωi,
то лишь конечное число индексов
ind (F, Ωi)
отлично от нуля и ind (F, Ω) =
∑∞i=1ind (F, Ωi).
|
3º. Если F(x)
≡ x0 и
x0 ∈ Ω, то
ind (F, Ω) = 1.
Один из фундаментальных результатов топологии — это факт
существования индекса неподвижных точек для любого
непрерывного невырожденного на
∂Ω отображения F:
Ω →
Rn.
В приложениях важнейшую роль играет следующее свойство индекса.
4º.
Если ind (F, Ω)
≠ 0, то отображение F имеет в
Ω по крайней мере одну
неподвижную точку.
Индекс легко вычисляется в случае, когда
F — линейный оператор, а
Ω — открытая ограниченная
окрестность нуля:
5º. Если
F — линейный оператор
в Rn, не имеющий единичного
собственного значения (это равносильно невырожденности F
на ∂Ω), то
ind (F, Ω) =
(–1)β,
где β —
сумма кратностей вещественных бóльших единицы
собственных значений оператора F.
Полезным в приложениях оказывается следующий признак
гомотопности двух отображений.
6º. Пусть
невырожденные на ∂Ω
отображения F0 и F1 таковы, что векторы
x – F0(x) и
x – F1(x)
направлены не противоположно при любых
x ∈ ∂Ω, т. е.
x – F0(x)
≠ λ[x
– F1(x)] при всех
λ < 0. Тогда F0
и F1 гомотопны.
Задача О32.1. Докажите, что в последнем случае
гомотопию осуществляет отображение
Φ(λ, x) =
(1 – λ)F0(x) +
λF1(x).
В случае, когда Rn = R2
индекс неподвижной точки можно определить наглядно. Допустим
∂Ω представляет собой замкнутую
жорданову кривую. Тогда
ind (F, Ω) — это
"число оборотов" вектора x – F(x),
когда точка x пробегает ∂Ω в положительном
направлении. Это определение формализуется так. Пусть φ:
[0, 1] →
R2 — параметризация ∂Ω,
причем, при возрастании t граница обходится в положительном
направлении. Обозначим через Ξ(t)
угол между полуосью Ox и вектором
φ(t) –
F[φ(t)]
(см. рис. 1);
здесь имеется в виду многозначная функция, значения которой в каждой
точке отличаются на 2πk
(k ∈ R). Пусть, наконец,
ξ — одна из непрерывных однозначных
ветвей функции Ξ. Тогда
ind (F, Ω) =
[ξ(1) –
ξ(0)]/2π (см. рис. 2).
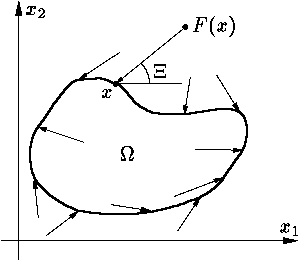
Рис. 1.
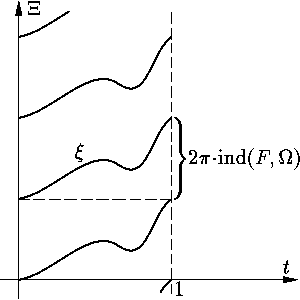
Рис. 2.
Задача О32.2. Пусть граница
∂Ω области Ω ⊂
R2 является гладкой замкнутой
жордановой кривой, а
отображение F: Ω
→ R2 таково, что вектор
x – F(x) при каждом x
∈ ∂Ω касателен к ∂Ω в
точке x. Докажите, что
ind (F, Ω) = 1.
В качестве первого примера применения теории
индекса докажем обещанную в очерке
"Динамические системы на плоскости"
теорему о существовании внутри
каждого цикла двумерной динамической системы стационарной точки. Итак,
пусть Γ — цикл двумерной
автономной системы
Обозначим через Ω внутренность цикла (таким
образом, ∂Ω = Γ).
Положим F(x) =
x – f(x).
Тогда, очевидно, вектор x – F(x) =
f(x) касателен к Γ.
Поэтому в силу задачи О32.2
ind (F, Ω) = 1,
а в силу свойства 4º
индекса отображение F имеет в Ω по крайней мере
одну неподвижную точку
x0: x0 =
x0 – f(x0),
и следовательно f(x0) = 0, что и требовалось.
Основная область приложений теории индекса в теории обыкновенных
дифференциальных уравнений — это теория
периодических решений. Стандартная схема такова. Рассмотрим задачу о
T-периодических решениях уравнения
|
Всюду ниже предполагается, что f:
R×Rn
→ Rn — непрерывное
T-периодическое по t (т. е.
f(t + T, x) ≡
f(t, x)) отображение и, кроме того,
F таково, что определен оператор
сдвига по траекториям этого уравнения (например, F удовлетворяет
условиям теоремы
Коши — Пикара). Задача о
T-периодических решениях уравнения (1)
эквивалентна задаче о неподвижных точках оператора
F = gT0
сдвига за период по траекториям уравнения (1). Точнее, если
x = φ(t) —
T-периодическое решение уравнения (1),
то x0 = φ(0) —
неподвижная точка оператора F и, наоборот, если
x0 — неподвижная точка
оператора F, то x(t) =
gt0(x0)—
T-периодическое решение уравнения
(1). |
Задача О32.3. Докажите это утверждение.
Таким образом, в силу свойства 4º индекса любой признак отличия
ind (F, Ω) от нуля является
признаком существования периодического решения уравнения (1)
с начальным значением, лежащим в Ω.
Основная трудность здесь — это необходимость
описывать такие признаки в терминах правой части F уравнения.
Один из эффективных приемов получения таких признаков — так
называемый метод направляющих потенциалов.
Для его описания напомним некоторые понятия.
Пусть V: Rn
→ R — непрерывно
дифференцируемая функция. Градиентом
функции V называется отображение grad V:
Rn → R,
задаваемое формулой
| grad V(x) = | ( |
∂V(x1, ...,
xn)
∂x1 |
, ..., |
∂V(x1, ...,
xn)
∂xn |
) |
; |
|
функцию V при этом называют потенциалом
отображения grad V. Потенциал V
называется невырожденным, если вне некоторого
шара (скажем радиуса ρ) с центром в нуле
отображение I – grad V
(здесь I — тождественное отображение)
невырождено.
Индексом ind V
невырожденного потенциала называется индекс
ind (I – grad V,
Ω) отображения
I – grad V на открытом
шаре Ω с центром в нуле, вне которого
отображение I – grad V
невырождено. Очевидно, ind V не зависит от
радиуса r шара Ω, если
r ≥ ρ (докажите!). Потенциал V
называется направляющим для уравнения
(1), если
при всех t и при всех x вне некоторого шара с центром в нуле
радиуса r0; здесь (·, ·) —
скалярное произведение в Rn. Другими словами, векторы
grad V(x) и
f(t, x) образуют острый угол.
|
Метод направляющих потенциалов основывается на следующем
утверждении, доказательство которого мы отпускаем, отсылая читателя
к специальной литературе (см., напр.,
[Красносельский,
Красносельский — Забрейко]).
Пусть V — направляющий потенциал для
уравнения (1), r ≥
r0, а Ω —
открытый шар радиуса r с центром в нуле. Тогда
ind (F, Ω) =
ind V, где F =
gT0—
оператор сдвига за период по
траекториям уравнения (1). Это утверждение
позволяет сводить вычисление ind (F,
Ω) к вычислению ind V,
что в ряде случаев оказывается значительно проще, поскольку
направляющий потенциал в некоторых случаях удается
выписать в явном виде. |
В качестве примера рассмотрим задачу о T-периодических
решениях уравнения
|
y′′ + ay′
+ φ(y) = ψ(t,
y, y′).
| (2) |
Уравнения такого вида встречаются в теории автоматического
регулирования. Предположим, что φ
и ψ — непрерывные удовлетворяющие
условию
Липшица по y и y′
функции, причем ψ является
T-периодической по t. Пусть
ψ(t, x1,
x2)
|x1| + |x2| |
→ 0 при |x1| +
|x2| → ∞. |
|
Положим
Покажем, что если κ1 < 0,
то уравнение (2) имеет по крайней мере одно T-периодическое
решение. Уравнение (2) эквивалентно системе
x′1=
x2
x′2=
–ax2 – φ(x1)
+ ψ(t, x1,
x2) | } |
= f(t, x1,
x2). |
|
(3) |
|
grad V(x) = (2ax1 +
2x2, 2x1), |
а
|
(grad V(x), f(t, x)) =
2x22–
x1φ(x1) + x1ψ(t, x1,
x2). |
Задача О32.4. Докажите, что потенциал V
невырожден и
ind V = 1.
Последнее гарантирует существование хотя бы одного
T-периодического решения системы (3) и,
следовательно, уравнения (2).
Задача О32.5. Докажите, что если a
≠ 0 и κ2 =
lim|y|→∞φ(y)/y
> 0, то направляющим потенциалом
системы (3) индекса 1 является функция
| V(x1, x2) =
–a3x21–
2a2x1x2 –
2ax22– 4a |
∫ |
x1
0 |
φ(ξ)
dξ. |
|
Во многих случаях использование оператора
сдвига затруднено именно тем, что его нельзя выписать в явном виде. Иногда
проще сводить задачу о T-периодических решениях уравнения
(1) к интегральным операторам. Например, указанная задача
эквивалентна задаче о неподвижных точках
действующего в C([0, T], Rn)
оператора
| [F(x)](t) = x(T) + |
∫ |
t
0 |
f[s,x(s)] ds. |
| (4) |
Задача О32.6. Докажите, что оператор F
действует в банаховом пространстве
C([0, T],
Rn), непрерывен и его неподвижные точки и только
они являются сужениями T-периодических решений уравнения
(1) на отрезок [0, T].
За простоту вида оператора приходится платить: мы вынуждены перенести
действие из конечномерного пространства
Rn
в бесконечномерное банахово пространство
C([0, T],
Rn). Эта плата оказывается не столь высокой,
поскольку получающиеся операторы оказываются в большинстве случаев
вполне непрерывными, а на вполне непрерывные операторы распространяется
теория индекса неподвижных точек. Поясним последнюю фразу и приведем один
пример. Для этого нам потребуются некоторые понятия и факты
функционального анализа.
Множество A в банаховом пространстве E
называется относительно компактным,
если из любой последовательности
{xk} ⊂ A
можно извлечь сходящуюся подпоследовательность.
Теорема Арцела — Асколи утверждает, что
множество в C([0, T],
Rn) относительно
компактно в том и только том случае, если оно равномерно
ограничено и равностепенно непрерывно. Непрерывный оператор
F: E → E
называется вполне непрерывным, если он переводит любое
ограниченное множество в относительно компактное.
Задача О32.7. Покажите, что определяемый
формулой (4) оператор F
вполне непрерывен как оператор в
C([0, T],
Rn).
Вышеприведенная фраза о том, что на вполне непрерывные операторы
переносится теория индекса неподвижных точек означает, что
для вполне непрерывных операторов F, определенных на
замыкании Ω ограниченной области
Ω в банаховом пространстве E и не имеющих на
∂Ω неподвижных точек, можно определить целое
число ind (F, Ω)
(индекс), обладающее свойствами
1º –
6º.
Рассмотрим теперь задачу о
T-периодических решениях обыкновенного дифференциального уравнения
|
x′ = A(t)x +
εf(t, x),
| (5) |
в котором F такая же, как и выше, а непрерывная
T-периодическая n×n-матрица-функция
A(t) такова, что линейное уравнение
не имеет нетривиальных T-периодических решений. Покажем, что при
достаточно малых ε уравнение
(5) имеет T-периодическое решение.
Задача о T-периодических решениях уравнения
(5) эквивалентна задаче о неподвижных
точках вполне непрерывного
в C([0,
T], Rn) оператора
| [Fε(x)](t) =
x(T) + | ∫ |
t
0 |
A(s)x(s) ds + ε |
∫ |
t
0 |
f[s, x(s)] ds. |
|
Пусть Ω — произвольный открытый шар в
C([0, T],
Rn) с центром в нуле (скажем
радиуса r). Отсутствие нетривиальных T-периодических
решений уравнения (6) означает, что единица не
является собственным числом
линейного оператора F0,
т. е. оператора Fε
при ε = 0. Поэтому в силу
свойства 5º индекса
ind (F0, Ω)
определен и отличен от нуля. Если мы теперь докажем, что векторы
x – F0(x) и
x – Fε(x)
при малых ε направлены
непротивоположно на ∂Ω, то тем самым покажем
отличие от нуля индекса
ind (F0, Ω)
(см. свойство 6º)
и, следовательно, существование
в Ω неподвижных точек
операторов Fε.
Для этого предположим противное: существуют
εk →
0, xk ∈ ∂Ω
(т. е. ||xk|| = r) и
λk < 0 такие, что
xk –
F0(xk) =
λk[xk –
Fεk(xk)]
или
| xk = |
1
1 – λk |
F0(xk) – |
λk
1 –
λk |
Fεk(xk). |
| (7) |
|
Заметим, во-первых, что поскольку оператор F0
вполне непрерывен, а последовательность
{xk} ограничена, последовательность
{F0(xk)}
относительно компактна и поэтому, не ограничивая
общности, ее можно считать сходящейся в
C([0, T],
Rn). Во-вторых, как легко видеть,
||Fεk(xk)
– F0(xk)||
→ 0.
Наконец, также не ограничивая общности, можно считать, что
последовательность {λk}
сходится к некоторому (конечному или бесконечному) числу
λ0. Из сказанного вытекает, что
последовательность, стоящая в правой части тождества (7),
сходится в C([0, T],
Rn), т. е. сходящейся к некоторому
x0 ∈ C([0, T],
Rn) является
последовательность {xk}, причем очевидно
x0 ≠ 0 так как
||xk|| = r. Переходя в
(7) к пределу при
k → ∞
и используя непрерывность F0, получаем |
что противоречит условиям. Таким образом, оператор
Fε при малых
ε имеет в Ω по крайней
мере одну неподвижную
точку, а вместе с этим и уравнение (5) при
малых ε имеет по крайней мере одно
T-периодическое решение.
Задача О32.8. Восстановите детали доказательства.
Задача О32.9. Покажите, что при малых
ε уравнение (5) имеет
T-периодическое решение xε такое,
что ||xε||C
→ 0.
Следует сказать в заключение, что топологические методы находят важные
приложения и в теории краевых задач, теории
бифуркаций, теории дифференциальных
уравнений с запаздывающим аргументом и т. д.
Литературные указания. В этом очерке термин "топологические
методы" использован в узком смысле: имеется в виду применение теории
индекса неподвижных точек. В более широком смысле связи теории
обыкновенных дифференциальных уравнений и топологии описаны, напр., в
учебниках [Арнольд,
Арнольд]. В указанном узком смысле
описанные методы восходят к классической статье Ж. Лере и
Ю. Шаудера (рус. пер. см. в Усп. матем. н., 1946, 1,
NN 3 – 4). Современное изложение можно найти в монографиях
[Красносельский,
Красносельский,
Красносельский —
Забрейко].
Задачи.
О32.10. Докажите, что если в автономном
уравнении
линейный оператор A невырожден, а непрерывный
оператор F ограничен на всем Rn
(||f(x)|| ≤ M
при всех x ∈
Rn), то уравнение имеет по крайней мере
одно стационарное решение.
|
О32.11. Точка x0 ∈
Rn называется точкой
T-невозвращаемости траектории уравнения (1), если
gt0(x0)≠
x0 при всех
t ∈ (0, T]. Пусть все точки
границы ∂Ω ограниченной области
Ω ⊂ Rn
представляют собой точки T-невозвращаемости траекторий уравнения
(1) и f(0, x) ≠
0 при x ∈ ∂Ω. Покажите, что
ind (gT0,
Ω) =
ind (I +
f(0,·), Ω)
(здесь через I + f(0,·)
обозначается отображение x → x +
f(0, x)). Поэтому любой признак отличия
ind (I + f(0, x), Ω)
от нуля в этих условиях является признаком наличия T-периодического
решения уравнения (1). |
О32.12. Пусть выполнены условия предыдущей задачи,
ind (I + f(0, x), Ω)
≠ 0, а требование существования и
непрерывности оператора сдвига
ослаблено до требования продолжимости
любого решения уравнения (1) на
отрезок [0, T] (под T-невозвращаемостью
точки x0 понимается теперь выполнение неравенства
x(t) ≠ x0
при всех t ∈ (0, T]).
Покажите, что уравнение (1) имеет по крайней мере
одно T-периодическое решение. (Указание:
аппроксимируйте f последовательностью удовлетворяющих
условию Липшица отображений).
О32.13. Индексом (изолированной)
неподвижной точки
вполне непрерывного оператора F,
действующего в банаховом пространстве E, называется число
ind (F, B(x0, r)), где
B(x0, r) — шар в E
радиуса r с центром в x0, не содержащий внутри себя и на
границе других неподвижных точек оператора F. Обозначение
ind (F, x0). Докажите, что определение
ind (F, x0) корректно, т. е.
не зависит от выбора шара B(x0, r).
О32.14. Рассмотрим задачу о
T-периодических решениях уравнения с параметром вида
где f: R×Rn×[0, 1]
→ Rn — T-периодическая по первому аргументу
непрерывная функция. Пусть при ε = 0
уравнение (8) имеет T-периодическое
решение x0 ненулевого индекса (под
индексом периодического
решения x0 здесь понимается
ind (F, x0),
где F — заданный формулой (4) оператор).
Покажите, что при достаточно малых ε
уравнение (8) имеет T-периодическое решение.
О32.15. Докажите, что в условиях предыдущей задачи при достаточно
малых ε уравнение (8) имеет
T-периодическое решение xε
такое, что ||xε –
x0||C → 0
при ε → 0.
О32.16. Рассмотрим краевую
задачу
|
x′′ +
a0(t)x′ +
a1(t)x = f(t, x,
x′),
t ∈ [0, T],
| (9) |
Предполагается, что функции a0,
a1 и F непрерывны. Пусть линейная задача
| x′′ +
a0(t)x′ +
a1(t)x = 0, t
∈ [0, T], |
имеет только нулевое решение и пусть
G(t, s) — ее
функция Грина. Пусть
для любой непрерывно дифференцируемой на [0, T]
функции φ функция
F(φ) определяется формулой
| [F(φ)](t) = |
∫ |
t
0 |
G(t, s)f[s,
x(s), x′(s)]
ds. |
|
(11) |
Докажите, что F действует в
C1[0, T]
и вполне непрерывен. Покажите, что решение задачи (9) –
(10) и только они являются
неподвижными точками оператора F.
О32.17. Покажите, что если F равномерно ограничена,
т. е. |f(t, a, b)|
≤ M при всех
t, a, b, то задача
(9) – (10)
имеет по крайней мере одно решение.
О32.18. Пусть задача (9) –
(10) имеет изолированное
решение x0 ненулевого индекса (индекс
неподвижной точки x0 действующего в
C1[0, T] оператора F
(см. (11)) отличен от нуля). Покажите, что
краевая задача
| x′′ +
a0(t)x′ +
a1(t)x =
εf(t, x,
x′), t
∈ [0, T], |
при всех достаточно близких к единице ε
имеет по крайней мере одно решение.
О32.19. Обобщите утверждение предыдущей задачи на случай
нелинейности вида f(t, x, x′,
ε).