§ О8. Первые интегралы

Вещественная функция V(t, x) определенная на открытом подмножестве D ⊂ R×Rⁿ называется первым интегралом (ср.) системы

x′ = f(t, x),

(1)

если вдоль любого решения φ этой системы, график которого целиком лежит в D, она сохраняет постоянное значение:

V[t, φ(t)] ≡ C.

Константа C не зависит от t, но, вообще говоря, зависит от решения φ.

Тривиальным примером первого интеграла для любой системы служит, очевидно, функция-константа V(t, x) ≡ a. Первые интегралы такого типа никакой информации о решении не несут и в дальнейшем исключаются из рассмотрения.

Нетривиальным примером первого интеграла для уравнения свободных колебаний линейного осциллятора (см.)

x′1= x2,    x′2= –ω2x1

(2)

является полная энергия осциллятора H = T + U, где T — кинетическая энергия T = x′12/2 = x22/2, а U — потенциальная энергия U = ω2x12/2 осциллятора. Действительно, если φ(t) = (φ1(t), φ2(t)) — решение системы (2), то

d dt H[φ(t)] = d dt ( φ22(t) 2   +   ω2φ12(t) 2 )   =

= φ2(t)φ′2(t)+ ω2φ1(t)φ′1(t)= φ2(t)[–ω2φ1(t)] + ω2φ1(t)φ2(t) = 0

и следовательно, H[φ(t)] ≡ const .

В этом случае первый интеграл дает бóльшую информацию о решениях — в фазовой плоскости они являются эллипсами.

Геометрически, первый интеграл — это такая функция, что любое решение лежит на одной и только поверхности уровня этой функции (см. рис. 1).

Рис. 1.

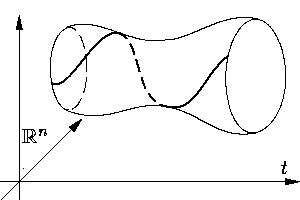
Вообще говоря, основным источником первых интегралов являются различные законы сохранения (энергии, как это было в вышеописанном примере осциллятора, импульса, момента импульса и т. п.)

Различие между двумя приведенными выше примерами первых интегралов характеризует следующее понятие невырожденности. Система непрерывно дифференцируемых первых интегралов V  = (V₁, ..., V_k) называется невырожденной на D, если в любой точке (t, x) ∈ D ранг ее производной ∂V/∂x равен числу k первых интегралов в этой системе.

Функция-константа представляет собой пример вырожденной системы первых интегралов (состоящей из одного интеграла), в то время как полная энергия линейного осциллятора есть невырожденная система первых интегралов на R²\{0}.

Задача О8.1. Докажите.

Системы первых интегралов называются иногда векторными, или k-мерными (если они состоят из k первых интегралов).

Задача О8.2. Докажите, что в условиях теоремы Коши — Пикара функции V₁(t, x) = x₁ и V₂(t, x) = t||x|| не могут быть одновременно первыми интегралами уравнения (1).

Задача О8.3. Докажите, что если двумерная система x′ = f(t, x) имеет на R×R2 два первых интеграла V1(t, x1, x2) = x12+ 2x22 и V2(t, x1, x2) = 2x12+ x22, то f(t, x) ≡ 0.

Основной смысл введенного понятия состоит в том, что невырожденный k-мерный первый интеграл позволяет локально выражать некоторые k неизвестных функций системы (1) через остальные. А именно, имеет место следующая

Теорема о понижении порядка. Пусть V — невырожденный k-мерный первый интеграл системы (1) на D, (t₀, x₀) ∈ D, C = (C₁, ..., C_k) = V(t₀, x₀). Тогда система уравнений

V(t, x) = C

в некоторой окрестности D₁ точки (t₀, x₀) однозначно разрешима относительно некоторого набора из k пространственных переменных, причем, получившаяся зависимость будет непрерывно дифференцируемой по совокупности переменных.

Д о к а з а т е л ь с т в о.  Пусть, для определенности, именно первые k столбцов якобиана ∂V/∂x определяют отличный от нуля минор и обозначим набор (x₁, ..., x_k) через y, а (x_k+1, ..., x_n) — через z. Тогда в новых обозначениях (здесь (y₀, z₀) = x₀)

y0, z0) = C,   det [ ∂V(t, y, z) ∂y ] | (t, y, z) = (t0, y0, z0) ≠ 0.

В силу теоремы о неявной функции уравнение

V(t, y, z) = C

в окрестности точки (t₀, y₀, z₀) однозначно разрешимо относительно y, а, точнее, в некоторой окрестности D₂ точки (t₀, z₀) найдется непрерывно дифференцируемая функция F: D₂ → R^k такая, что

V[t, F(t, x), z] = C.

при всех (t, z) ∈ D₂, что и требовалось.

В общем случае процедура понижения порядка выглядит следующим образом. Перепишем систему (1) в переменных y и z:

y′ = f1(t, y, z), z′ = f2(t, y, z),

(3)

где f(t, x) = f(t, y, z) = (f₁(t, y, z), f₂(t, y, z)). Поскольку вдоль решения, выпущенного в момент времени t₀ из точки (y₀, z₀), первый интеграл сохраняет значение C (= V(t₀, y₀, z₀)):

V[t, y(t), z(t)] = C,

в силу теоремы о понижении порядка в окрестности точки t₀

y(t) = F[t, z(t)].

(2)

Подставив (4) во второе уравнение системы (3), получим систему n – k дифференциальных уравнений с n – k неизвестными

z′ = f2[t, F(t, z), z].

Компонента y решения системы (3) находится по z из (4).

Задача О8.4. Понизьте порядок системы (2), описывающей колебания линейного осциллятора.

Таким образом, наличие невырожденного первого интеграла позволяет понижать порядок системы.

Признак первого интеграла можно сформулировать в терминах дифференциальных уравнений в частных производных первого порядка. А именно, для того, чтобы непрерывно дифференцируемая вектор-функция V(t, x) была первым интегралом системы (1) на D необходимо и достаточно, чтобы при всех (t, x) ∈ D выполнялось равенство

∂V(t, x) ∂t + ∂V(t, x) ∂x f(t, x) = 0.

(5)

Для  д о к а з а т е л ь с т в а  достаточности нужно заметить только, что если φ — решение (1), лежащее в D, то V[t, φ(t)] = const и следовательно

0 = dV[t, φ(t)] dt = ∂V(t, x) ∂t | x = φ(t) + ∂V(t, x) ∂x | x = φ(t) f[t, φ(t)].

Докажем необходимость. Пусть (t0, x0) ∈ D, а φ(t) = gt0t(x0)— решение системы (1), проходящее через точку (t0, x0). Тогда, поскольку V[t, φ(t)] = const при всех t достаточно близких к t0,

dV[t, φ(t)] dt | x = t0 = 0.

Последнее равенство равносильно следующему

∂V(t, x) ∂t | (t, x) = (t0, φ(t0)) + ∂V(t, x) ∂x | (t, x) = (t0, φ(t0)) f[t0,φ(t0)] = 0,

которое в силу произвольности (t₀, x₀) эквивалентно (5).

Например, если k = 1, то равенство (5) в подробной записи выглядит так:

∂V(t, x) ∂t  + f1(t, x) ∂V(t, x) ∂x1  + ... + fn(t, x) ∂V(t, x) ∂xn  = 0.

Последнее равенство, если его рассматривать как уравнение относительно неизвестной функции V от n + 1 переменной, представляет собой линейное дифференциальное уравнение в частных производных первого порядка (соответственно, равенство (5) представляет собой систему k линейных дифференциальных уравнений в частных производных первого порядка ).

Таким образом, понятие первого интеграла, в частности, устанавливает связь между системами обыкновенных дифференциальных уравнений и линейными уравнениями в частных производных первого порядка.

Для невырожденной системы k первых интегралов, очевидно, выполнено неравенство k ≤ n (n — размерность системы (1)). Невырожденная система, состоящая ровно из n скалярных первых интегралов называется полной системой , или полным первым интегралом.

В силу теоремы о понижении порядка полный первый интеграл позволяет в принципе (т. е. через теорему о неявной функции) локально выразить все неизвестные функции через t, т. е. локально найти все решения (см. рис. 2). Таким образом, знание полного первого интеграла позволяет найти общее решение. Имеет место и обратное утверждение: полный первый интеграл можно найти через общее решение (это не такая бессмысленная задача, как это может показаться на первый взгляд; например знание первого интеграла может оказаться полезным при изучении уравнений в частных производных).

Рис. 2.

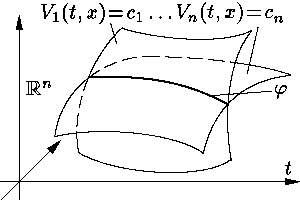
Теорема о существовании полного первого интеграла. Пусть выполнены условия обобщенной теоремы Коши — Пикара, функция f непрерывно дифференцируема и, кроме того, ее производная удовлетворяет условию Липшица по совокупности переменных. Тогда вектор-функция

V(t, x) = gt0t(x)

(6)

(t₀ — произвольный фиксированный момент времени) является полным первым интегралом системы (1).

Д о к а з а т е л ь с т в о.  Пусть φ — решение системы (1). Тогда

V[t, φ(t)] = gt0t[φ(t)] = gt0t·gt0t[φ(t0)] = gtt[φ(t0)] = φ(t0)

и следовательно не зависит от t. Написанная цепочка равенств геометрически совсем очевидна — задаваемая формулой (6) функция V(t, x) сопоставляет каждой точке (t, x) расширенного фазового пространства значение в точке t₀ решения, проходящего в момент времени t через x; поэтому значение функции V(t, x) на любом решении равно значению этого решения в момент времени t₀ и, таким образом, константа.

Дифференцируемость функции V вытекает из теорем о дифференцируемости оператора сдвига, а невырожденность следует из того, что ∂V/∂x = (∂/∂x)gt0t(x) является оператором сдвига по траекториям (линейного) уравнения в вариациях вдоль решения gt0t(x); оператор же сдвига по траекториям линейного уравнения невырожден.

Задача О8.5. Пусть Φ — фундаментальная матрица линейной системы x′ = A(t)x с непрерывной матрицей-функцией A(t). Докажите, что V(t, x) = Φ^–1(t)x является полным первым интегралом этой системы.

Полные первые интегралы являются в некотором смысле базисами во множестве всех первых интегралов. Более точно, имеет место следующая

Теорема об общем виде первого интеграла. Пусть выполнены условия предыдущей теоремы и пусть V(t, x) — полный первый интеграл, определенный в некоторой окрестности точки (t₀, x₀). Тогда любой скалярный первый интеграл V(t, x), определенный в некоторой окрестности этой точки может быть представлен в виде

V(t, x) = F[V(t, x)]

с непрерывно дифференцируемой функцией F.

Д о к а з а т е л ь с т в о.  По определению первого интеграла для любого x величины V[t, gt0t(x)] и V[t, gt0t(x)]— константы, зависящие только от x. Обозначим их через W(x) и W(x), соответственно. Таким образом, для y = gt0t(x)

V(t, y) = W(x),

(7)

и

V(t, y) = W(x).

(8)

Заметим теперь, что производная ∂ W(x)/∂x невырождена как суперпозиция невырожденных операторов:

∂W(x) ∂x = ∂V(t, y) ∂y | y = gt0t(x) · ∂ ∂x gt0t(x).

Поэтому, в силу теоремы о неявной функции, отображение W обратимо в окрестности точки x₀. Из (7) следует, что

x = W–1[V(t, y)].

Но тогда, учитывая (8), получаем

V(t, y) = W(x) = W ( W–1[V(t, y)] ) = F[V(t, x)],

где F = W·W^–1. Учитывая произвольность y, получаем требуемое представление. Непрерывная дифференцируемость F очевидна.

Задача О8.6. Восстановите детали доказательства. В частности, почему y можно считать произвольным в некоторой окрестности точки (t₀, x₀)?

Для автономных систем

x′ = f(x)

(9)

(f: Rⁿ → Rⁿ) интересен вопрос о существовании автономных (т. е. не зависящих от t) первых интегралов.

Теорема об автономных первых интегралах. Пусть функция f непрерывно дифференцируема и ее производная удовлетворяет условию Липшица. Пусть x₀ — неособая точка системы (9), т. е. f(x₀) ≠ 0. Тогда в некоторой окрестности D точки x₀ существует (n – 1)-мерный невырожденный автономный первый интеграл V системы (9). Любой автономный скалярный первый интеграл V в некоторой окрестности точки x₀ может быть выражен в виде

V(x) = F[V(x)]

с помощью непрерывно дифференцируемой функции F.

Д о к а з а т е л ь с т в о.  Так как f(x₀) ≠ 0, не ограничивая общности, можно считать, что, например, первая координата f₁ функции f отлична от нуля в точке x₀, а следовательно, и в некоторой окрестности D этой точки. Сделаем в (9) замену переменных, принимая координату x₁ за новое "время"; получим (n – 1)-мерную (неавтономную) систему уравнений

dx2 dx1  =  f2(x1, ..., xn) f1(x1, ..., xn) , · · · dxn dx1  =  fn(x1, ..., xn) f1(x1, ..., xn) .

(10)

По предыдущей теореме у системы (10) существует полный ((n – 1)-мерный) невырожденный первый интеграл. В окрестности D он, очевидно, является искомым невырожденным автономным первым интегралом системы (9). Представление произвольного скалярного интеграла также вытекает из упомянутой теоремы.

Геометрически, в случае двумерной системы, данная теорема означает, что локально график каждого решения лежит на цилиндрической поверхности с образующей параллельной оси времени и линией уровня первого интеграла в фазовой плоскости в качестве направляющей (см. рис. 3). В общем случае эта цилиндрическая поверхность получается, если в качестве направляющей взять кривую, являющуюся пересечением поверхностей уровня n – 1 скалярного первого интеграла в фазовом пространстве, все с той же параллельной оси времени образующей.

Рис. 3.

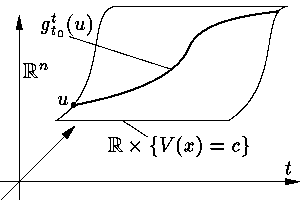
Если перенести рассмотрения из расширенного фазового пространства в фазовое пространство, то последняя теорема утверждает, что локально траектории системы лежат на кривой, получающейся в результате пересечения поверхностей уровня n – 1 скалярного автономного первого интеграла.

В окрестности особой точки (т. е. положения равновесия системы) автономные невырожденные первые интегралы могут и не существовать.

Задача О8.7. Приведите пример.

Литературные указания. Понятие первого интеграла относится к базовым понятиям теории обыкновенных дифференциальных уравнений. Поэтому их описание можно найти фактически в каждом учебнике; см., напр., [Арнольд, Бибиков, Картан, Карташов — Рождественский, Петровский, Понтрягин, Тихонов — Васильева — Свешников, Федорюк, Хартман].

Задачи. О8.8. Автономная система 2n уравнений

p′i = – ∂H ∂qi ,   q′i = ∂H ∂pi

(i = 1, ..., n), где H — дважды непрерывно дифференцируемая функция 2n аргументов p₁, ..., p_n, q₁, ..., q_n называется гамильтоновой системой. Покажите, что функция H (гамильтониан) является ее первым интегралом.

О8.9. Пусть для уравнений x′ = f(t, x) и x′ = g(t, x) выполнены условия теоремы Коши — Пикара. Докажите, что если эти уравнения имеют общий полный первый интеграл, то они совпадают.

О8.10. При каких a двумерная система

x′1= x1,    x′2= ax2

имеет в окрестности нуля D невырожденный в D\{0} скалярный автономный первый интеграл?

О8.11. Пусть автономная система (9) имеет на Rⁿ автономный полный первый интеграл V, причем ||V(x)|| → ∞ при ||x|| → ∞. Докажите, что любое решение этой системы ограничено на R₊.

О8.12. Докажите, что если в уравнении (9) функция f непрерывно дифференцируема, f(0) = 0, а f ′(0) имеет собственное значение с положительной вещественной частью, то функция V(x) = ||x|| не может быть первым интегралом этого уравнения.

О8.13. Покажите, что если A*B + B*A = 0, то квадратичная форма V(x) = (Bx, x) есть первый интеграл системы x′ = Ax.

О8.14. Докажите обратное утверждение: если V(x) = (Bx, x) — первый интеграл системы x′ = Ax, то A*B + B*A = 0.

О8.15. Проверьте, что момент импульса K = mr×r′ (× — векторное произведение в R³) есть трехмерный первый интеграл системы уравнений движения материальной точки в центральном силовом поле

r′′ = f(||r||)r,

где r = (x, y, z), || r || = (x² + y² + z²)^1/2.

О8.16. В условиях задачи О8.15 движение точки происходит в неподвижной плоскости, определяемой начальным положением и начальной скоростью точки.

О8.17. В условиях задачи О8.15 покажите, что импульс mv = mr′ материальной точки не является первым интегралом системы.

О8.18. Покажите, что полная энергия E = (mv²)/2 + mgh является, а кинетическая энергия T = (mv²)/2 не является первым интегралом уравнения колебаний маятника

φ′ = ω,    ω′ = – g l sin φ.

File based on translation from T_EX by T_TH, version 2.32.
Created 17 Jan 2000, 14:22.
Last modified 24 Apr 2002.