§ 1.1. Основные понятия

В этом параграфе описывается общий вид обыкновенных дифференциальных уравнений (ОДУ) и вводятся такие понятия, как решение, следование, эквивалентность, общее решение, интегралы ОДУ.

1.1.1. Примеры ОДУ. а) Известную из математического анализа задачу отыскания всех первообразных данной функции f можно записать в виде уравнения

y′ = f(x),

(1)

где f — данная непрерывная функция, y = y(x) — неизвестная функция, y′ = dy/dx; оно представляет собой простейший пример ОДУ. Как доказывается в интегральном исчислении, если f непрерывна на промежутке J, то уравнение (1) имеет на нем бесконечное семейство решений, которое задается формулой

y = F(x) + C;

(2)

здесь F — какая-нибудь фиксированная первообразная функции f, а параметр C пробегает все вещественные значения.

б) Замечательным свойством функции y = e^x является то, что она совпадает со своей производной; это свойство записывается в виде ОДУ

y′ = y,

(3)

решениями которого, наряду с e^x, будут все функции семейства

y = Cex.

(4)

в) С учетом механического смысла второй производной (ускорение) уравнение прямолинейного равноускоренного движения записывается в форме

x.. = a.

(5)

Точками здесь (и часто в дальнейшем) обозначаются производные по времени. Последовательное интегрирование (5) в пределах от 0 до t дает:

x. = at + v0    (v0 = x.(0)),

(6)

x =  at2 2   + v0t + x0    (x0 = x(0)).

(7)

г) Если в уравнении окружности

x2 + y2 = R2

(8)

переменные x и y считать гладкими функциями параметра s: x = x(s), y = y(s) — и продифференцировать (8) по s, то получится дифференциальное уравнение семейства всех окружностей с центром в начале координат:

x dx ds  + y dy ds  = 0.

(9)

д) Одним из решений уравнения (9) является пара функций

x = sin s, y = cos s.

(10)

Очевидно, эта пара удовлетворяет также следующей системе дифференциальных уравнений:

x′ = y, y′ = –x.

(11)

1.1.2. Общий вид ОДУ. В общей ситуации мы, как правило, будем обозначать значения неизвестной функции буквой x, независимой переменной — t (и интерпретировать ее как время), производных от x по t — x′, x′′, ..., x^(m). Мы будем также использовать сокращенное обозначение J^(m)x = (x, x′, ..., x^(m)) — этот вектор называют струей, или джетом m-го порядка функции x в точке t. В дифференциальные уравнения может входить также набор C = (C₁, C₂, ..., C_p) произвольных постоянных (параметров). Тогда произвольное ОДУ с одной неизвестной функцией может быть, по определению, записано в виде

F(t, J(m)x, C) = 0.

(12)

Когда нужно подчеркнуть наличие в уравнении параметра C мы будем говорить о семействе ОДУ, зависящих от параметра C = (C₁, C₂, ..., C_p).

Наряду с такими уравнениями мы будем рассматривать системы ОДУ с несколькими неизвестными:

F1(t, J(m)x, C) = 0, F2(t, J(m)x, C) = 0, . . . Fk(t, J(m)x, C) = 0;

(13)

в нем теперь

x = (x1, x2, ..., xn), m = (m1, m2, ..., mn), J(m)x = ( J(m1)x1, J(m2)x2, ..., J(mn)xn), J(mi)xi = (xi, x′i,..., xi(m1)).

(14)

Числа m_i называются порядками системы (13) по неизвестной функции x_i, а |m| = m₁ + m₂ + ... + m_n — просто порядком системы.

В некоторых случаях бывает полезно приписывать уравнению бóльшие порядки, чем непосредственно следующие из его записи. Например, если к семейству уравнений (8) приписать условие "x, y ∈ D¹" (x и y имеют производные первого порядка), то оно становится эквивалентным уравнению (9); без этого условия у (8) решений больше, чем у (9).

Если в (12) допускать, чтобы F принимало векторные значения (в R^k) и под J^(m)x понимать набор переменных (14), то (12) есть сокращенная запись (13). Именно так, если не оговорено противное, впредь будет пониматься уравнение (12) — как векторная запись системы из k скалярных уравнений с n скалярными неизвестными функциями.

Подробная запись системы (13) выглядит так:

F1(t, x1, x′1,..., x1(m1),..., xn, x′n,..., xn(mn),C1, C2, ..., Cp) = 0, F2(t, x1, x′1,..., x1(m1),..., xn, x′n,..., xn(mn),C1, C2, ..., Cp) = 0, . . . Fk( t, x1, x′1,..., x1(m1),..., xn, x′n,..., xn(mn),C1, C2, ..., Cp) = 0,

Мы будем рассматривать и ОДУ нулевого порядка, называя их обыкновенными функциональными уравнениями. Например, (2), (4), (7), (10) — это обыкновенные функциональные уравнения (если быть точными, первые три из них являются семействами уравнений, зависящих от параметров C или (v₀, x₀)).

Для некоторых примеров из 1.1.1 приведем таблицу соответствия с обозначениями, принятыми в общем уравнении (12).

1.1.3. Уравнения, разрешенные относительно старшей производной. Иногда уравнение (12) можно разрешить относительно старших производных, хотя общего способа для этого не существует:

x(m) = f(t, J(m–1)x, C)

(15)

Здесь использованы новые обозначения

x(m) = (x1(m1),x2(m2),..., xn(mn))

m – 1 = (m1 – 1, m2 – 1, ... , mn – 1).

Если m = (1, 1, ..., 1), то в правую часть (15) производные вообще не входят. Уравнение (15) в этом случае и при отсутствии вектора произвольных постоянных C называют нормальной системой (нормальным уравнением), или системой в нормальной форме, или системой в форме Коши:

x′ = f(t, x).

(16)

Ниже мы докажем, что (15) путем увеличения числа неизвестных всегда можно привести к нормальной форме (16). Именно нормальная система (16) является основным объектом изучения в теории обыкновенных дифференциальных уравнений. Однако, в настоящей главе, изучая элементарную теорию, мы будем иногда иметь дело с более общей системой (12).

В рассмотренных выше примерах (1), (3), (11) — нормальные системы, причем первые две имеют порядок 1, а последняя — 2. Уравнение (5) — уравнение второго порядка, разрешенное относительно старшей производной.

Подчеркнем характерную особенность обыкновенных дифференциальных уравнений, отличающую их от прочих уравнений, содержащих производные неизвестных функций: все неизвестные должны быть функциями одного вещественного аргумента и все они и их производные должны входить в уравнение только в виде своих значений в одной и той же переменной точке (в наших обозначениях — в точке t), которая также может фигурировать в уравнении. Вот примеры нарушения этих требований:

∂u ∂x + ∂u ∂y = 0

(неизвестная u — функция двух аргументов x и y; это пример дифференциального уравнения в частных производных),

x′(t) = x(t – 1),

x′(t) = ∫ t t0 x(s) ds

(неизвестная функция и ее производная входят в уравнение в виде значений в разных точках t, t – 1 и s ∈ [t₀, t]; это представители так называемых дифференциально-разностных и дифференциально-интегральных уравнений). Ни одно из приведенных трех дифференциальных уравнений не называют обыкновенным.

1.1.4. Определение решения. Понятие "решения ОДУ" уже использовавшееся в 1.1.1, формально определяется для уравнения (12) так: это определенная на промежутке D(φ) функция x = φ(t), которая при подстановке в уравнение обращает его при некотором значении C в тождество относительно t ∈ D(φ): ∃(C)∀(t ∈D(φ)) [F(t, J^(m)x, C) = 0].

Несколько замечаний о терминологии и обозначениях. Обозначение D(φ) будет использоваться как стандартное для области определения функции φ. Под промежутком понимается любой не сводящийся к одной точке отрезок, интервал или полуинтервал, который может быть неограниченным в одну или обе стороны; другими словами, любое связное подмножество вещественной оси R, содержащее более одной точки. Требование связности области определения не всегда включается в определение решения, однако оно удобно, так как облегчает описание множества всех решений. Например, как говорилось в 1.1.1, множество всех решений уравнения (1) на промежутке J описывается формулой (2). Это следствие основной леммы интегрального исчисления, которая гласит: если y′ = 0 на каком-либо промежутке, то на нем y ≡ C. Для множества, состоящего, скажем, из двух не пересекающихся интервалов, это уже не справедливо.

Определение решения включает в себя требование возможности подстановки φ в (12), т. е. условие (t, J^(m)x|_x=φ(t), C) ∈ D(φ) при всех t ∈ D(φ); в частности, должны существовать все производные от φ_i до порядка m_i включительно (i = 1, ..., n).

Подчеркнем, что решения семейства ОДУ — это решения всех входящих в него уравнений (при всех возможных значениях параметра). Например, y = e^x и y = e^2+x — решения семейства (4). Не все параметры, входящие в запись уравнения, считаются параметрами семейства, это нужно оговаривать специально. Например в (7) v₀ и x₀ — параметры семейства, а a — параметр, который мы будем называть фиксированным. Различие состоит именно в определении решения: x = at²/2 – t + 1 — решение семейства (7), а x = t²/2 – t + 1 является решением семейства лишь при условии a = 1.

1.1.5. Следование, эквивалентность. Говорят, что из ОДУ У1 следует уравнение У2 (и пишут У1 ⇒ У2), если любое решение первого является и решением второго. По определению, два ОДУ У1 и У2 эквивалентны, если из первого следует второе и из второго — первое (У1 ⇔ У2).

Например, из системы (11) следует уравнение (9). Действительно, если умножить первое из уравнений (11) на x, а второе на y и результаты сложить, то получится (9). Итак, (11) ⇒ (9). С другой стороны, (9) (11), так как, например, решение-константа x = y = 1 уравнения (9) не удовлетворяет системе (11). Поэтому (11) (9). Переход от (5) к (6) и к (7) является, как нетрудно видеть, эквивалентным: (5) ⇔ (6) ⇔ (7).

В связи с понятиями следования и эквивалентности уточним, что решением ОДУ мы будем называть не функцию φ, а уравнение x = φ(t), содержащее обозначения переменных x, t. Это означает, в частности, что уравнения y′ = f(x) и z′ = f(t) мы не считаем эквивалентными, хотя им удовлетворяют одни и те же функции. В подобных ситуациях будем говорить, что эти уравнения эквивалентны с учетом замены переменных y = z, x = t. Существенность этого замечания проявляется, например, при замене одного из уравнений системы на эквивалентное.

1.1.6. Терминология, связанная с решениями и интегралами ОДУ. Наряду с (12) рассмотрим уравнение

F(t, J(m)x, C) = 0,

(17)

в котором

|m| < |m|.

(18)

Будем называет его по отношению к (12) частичным решением, если (17) ⇒ (12), интегралом, если (12) ⇒ (17) и эквивалентным интегралом, если (17) ⇔ (12).

Например, всякое решение (≡ частное решение) в смысле определения 1.1.4 с уточнением в 1.1.6, является частичным решением, но, вообще говоря, не является интегралом. Уравнение (8) с произвольной постоянной R есть интеграл уравнения (9), а с дополнительным условием x, y ∈ D¹ — эквивалентный интеграл.

Если интеграл (17) имеет вид

Φ(t, J(m)x) = C

(19)

то его левую часть также называют интегралом уравнения (12). Например,

Φ(x) = ∫ t t0 f(ξ) dξ

есть (эквивалентный) интеграл уравнения (1). Если эквивалентный интеграл (17) имеет нулевой порядок, то будем называть его полным интегралом. Полный интеграл, разрешенный относительно x, т. е. имеющий вид

x = φ(t, C),

называется общим решением. Интеграл (17) называют первым, если |m| = |m| – 1 (а иногда — если m = m – 1). Вообще границы применения перечисленных терминов в литературе достаточно мягкие; мы будем придерживаться установленных здесь соглашений.

1.1.7. Об интегрировании ОДУ в квадратурах. Выражение общего решения или полного интеграла через элементарные функции и интегралы от них называют интегрированием данного ОДУ в квадратурах (термин "квадратура" в данной ситуации означает взятие неопределенного интеграла, а "интегрирование" — нахождение полного интеграла). Интегрирование в квадратурах допускают лишь уравнения некоторых простейших типов. Большинство же ОДУ можно решать только приближенно или исследовать их качественными методами, то есть методами, позволяющими выяснять свойства решений без явного их отыскания. Качественные и приближенные методы составляют основное содержание современной теории обыкновенных дифференциальных уравнений.

Здесь мы рассмотрим два простейших приближенных метода, которые, помимо своей чисто прикладной ценности, полезны еще тем, что позволяют связать с основными понятиями теории обыкновенных дифференциальных уравнений систему простых наглядных представлений.

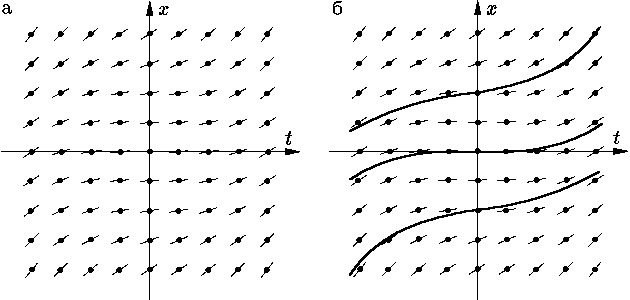
1.1.8. Геометрическая интерпретация ОДУ. Графики решений x = φ(t) скалярного ОДУ первого порядка, разрешенного относительно производной

x′ = f(t, x),

(20)

называются его интегральными кривыми. В геометрических терминах уравнение (20) выражает следующий факт: кривая на (t, x)-плоскости является его интегральной кривой в том и только том случае, когда в любой точке (t₀, x₀) этой кривой она имеет касательную с угловым коэффициентом k = f(t₀, x₀).

Таким образом, зная правую часть уравнения (20), мы можем заранее построить касательные ко всем интегральным кривым во всех точках: для этого каждой точке (t₀, x₀) нужно сопоставить проходящую через нее прямую с угловым коэффициентом k = f(t₀, x₀). Полученное соответствие между точками плоскости и проходящими через нее прямыми называется полем направлений уравнения (20). Конечно, фактически поле направлений можно построить лишь в виде достаточно густой сетки отрезков с отмеченными на них точками (см. рис. 1а). После этого задача построения интегральных кривых становится похожей на отыскание нужного пути в большом парке, снабженном густой сетью стрелок-указателей (рис. 1б).

Рис. 1.

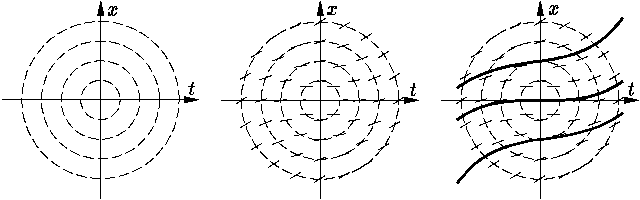
1.1.9. Метод изоклин. Построение поля направлений значительно облегчается предварительным нахождением изоклин — кривых на (t, x)-плоскости, вдоль которых угловой коэффициент k сохраняет неизменное значение. Уравнение изоклин имеет вид

f(t, x) = k;

вдоль изоклин отрезок, принадлежащий полю направлений, переносится параллельно своему первоначальному положению: переход к другой изоклине осуществляется изменением k и построением отрезка с новым угловым коэффициентом.

Например, для уравнения

x′ = t2 + x2

изоклины описываются уравнением

t2 + x2 = k.

Это — семейство концентрических окружностей с центром в начале координат. На рис. 2 изображен процесс последовательного построения изоклин, поля направлений и интегральных кривых.

Метод изоклин как средство эскизного представления интегральных кривых сохраняет свое значение и в нынешнюю эпоху бурного развития вычислительных машин и вычислительных методов.

Рис. 2.

1.1.10. Метод ломаных Эйлера. Метод ломаных применяется для приближенного нахождения значений x_i = φ(t_i) решения φ на некоторой сетке значений аргумента t: t₀, t₁ = t₀ + τ, t₂ = t₁ + τ, φ, t_n = t_n–1 + τ; τ — заданное положительное число, называемое шагом сетки. В применении к уравнению (20) этот метод заключается в следующем. В точке t = t_i–1 (20) принимает вид

x′i–1 = f(ti–1, xi–1).

Заменим здесь приближенно x′_i–1 конечно-разностным отношением

xi – xi–1 τ ≈ f(ti–1, xi–1)

и выразим x_i:

xi ≈ xi–1 + τf(ti–1, xi–1).

Если x₀ = φ(t₀) задать произвольно, то полученная рекуррентная формула позволяет приближенно найти значения x₁, x₂, ... .

Рис. 3.

Возвращаясь к образу парка со стрелками-указателями, метод ломаных Эйлера можно представлять себе так (см. рис. 3): из точки (t₀, x₀) мы движемся, сообразуясь с указателем, помещенным в этой точке в течение "τ секунд". Придя (через время τ) в точку (t₁, x₁), мы меняем направление, пользуясь указателем в этой точке; через время τ мы приходим в точку (t₂, x₂), опять меняем направление, и т. д.

Конечно, точность этого метода нуждается в специальном обосновании, которое мы проводить не будем. Кажется весьма правдоподобным (и оказывается в широких предположениях об f(t, x) верным) тот факт, что при τ → 0 погрешность метода ломаных Эйлера стремится к нулю на любом конечном промежутке изменения t.

В отличие от метода изоклин, метод ломаных Эйлера применим и к уравнениям более высокого порядка. Например, для уравнения

x′′ = f(t, x, x′)

он принимает вид

xi – xi–1 τ  –  xi–1 – xi–2 τ τ ≈ f ( ti–1, xi–1, xi–1 – xi–2 τ ) .

Из этого приближенного равенства нужно выразить x_i через x_i–1, x_i–2 и t_i–1. Заметим, что для использования получившейся рекуррентной формулы нужно задать не только x₀ = φ(t₀), но и x₁ = φ(t₁) (или φ′(t₀) в разностной записи).

Это наводит на следующую догадку, которая впоследствии будет доказана: для выделения определенного решения скалярного уравнения m-го порядка достаточно задать в некоторой точке t₀ значение самогó решения и его производных до порядка m – 1 включительно. Система

x(m) = f(t, x, x′, ..., x(m–1)), x(t0) = x0, x′(t0) = x1, ... x(m–1)(t0) = xm–1

называется начальной задачей или задачей Коши. Упомянутая выше гипотеза заключается в том, что при естественных предположениях относительно f она имеет единственное решение.

В качестве примера решим методом Эйлера задачу Коши

x′ = ax, x(0) = x0    (a, x0 — параметры).

Фиксируем t ≠ 0 и положим τ = t/n (n ∈ N). Тогда

xi ≈ xi–1 + τaxi–1 = ( 1 + at n ) xi–1 ≈ ( 1 + at n ) i x0.

Следовательно,

x(t) ≈ xn ≈ ( 1 + at n ) i x0.

Полученное приближенное значение при n → ∞ стремится к функции e^atx₀, которая, как легко проверить, точным решением рассматриваемой задачи Коши.

1.1.11. Контрольные вопросы

1.1.11.1. Является ли уравнение x′(t) = x(x(t)) обыкновенным дифференциальным?

1.1.11.2. Является ли функция φ(t) = |t| решением ОДУ tx′ = x на промежутке [–1, 1]?

1.1.11.3. Пусть функции x = φ(t) и x = ψ(t) являются решениями дифференциального уравнения x′ = f(t, x) на отрезках [–1, 0] и [0, 1], соответственно, и φ(0) = ψ(0). Является ли функция

x = φ(t), если t ∈ [–1, 0], ψ(t), если t ∈ [0, 1]

решением этого уравнения на отрезке [–1, 1]?

1.1.11.4. Верно ли следующее утверждение: если уравнение x′ = f(t, x) есть следствие уравнения x′ = g(t, x), то любой интеграл первого уравнения является интегралом второго?

1.1.11.5. Верно ли следующее утверждение: если уравнение x′ = f(t, x) есть следствие уравнения x′ = g(t, x), то любое частичное решение первого уравнения является частичным решением второго? А наоборот?

1.1.11.6. Как выглядят изоклины уравнений x′ = g(t) и x′ = f(x)?

1.1.11.7. Найдите изоклины и нарисуйте интегральные кривые уравнений x′ = x/t и x′ = –t/x.

1.1.11.8. Найдите ломаную Эйлера на отрезке [0,1] с шагом τ = 0.2 для задачи Коши x′ = tx, x(0) = 1.

1.1.12. Задачи

1.1.12.1. Докажите, что функция φ(t) = cos t (t ∈ R) не может быть решением уравнения вида x′ = t²g(x).

1.1.12.2. Могут ли функции φ(t) = sin t (–π/2 < t < π/2) и ψ(t) = cos t (2π < t < 3π) быть решениями одного и того же уравнения вида x′ = f(x)?

1.1.12.3. Могут ли функции φ(t) = sin t и ψ(t) = cos t (t ∈ R) быть решениями одного и того же уравнения вида x′′ + a₁x′ + a₀x = 0?

1.1.12.4. Покажите, что если x = φ(t) — решение уравнения вида x′ = f(x)cos²t, то x = φ(t + π) также является его решением.

1.1.12.5. Пусть функция f: [a, b] → R непрерывна на [a, b]\{t₀} (t₀ ∈ (a, b)) и разрывна в точке t₀. Может ли уравнение x′ = f(t) иметь определенное на [a, b] решение? А если в t₀ разрыв первого рода?

1.1.12.6. Покажите, что любое решение φ уравнения x′ = f(t, x) с непрерывной функцией f непрерывно дифференцируемо.

1.1.12.7. Имеет ли место аналогичное утверждение для уравнения f(t, x, x′) = 0?

1.1.12.8. Докажите, что если функция f непрерывно дифференцируема k раз, то любое решение φ уравнения x′ = f(t, x) непрерывно дифференцируемо k + 1 раз.

1.1.12.9. Покажите, что если x = φ(t, C) и y = ψ(t, C) — общие решения уравнений x′ = f(t, x) и y′ = g(t, x), соответственно, то (x, y) = (φ(t, C₁), ψ(t, C₂)) — общее решение системы, составленной их двух указанных уравнений.

1.1.12.10. Докажите, что если функции x = φ(t) и x = ψ(t) являются решениями дифференциального уравнения x′ = f(t, x) на отрезке [a, b], то функции x = max{φ(t), ψ(t)} и x = min{φ(t), ψ(t)} также являются решениями этого уравнения на данном отрезке.

1.1.12.11. Пусть функция f: R×R → R непрерывна и при tx ≠ 0 удовлетворяет условию txf(t, x) < 0. Докажите, что любое решение φ уравнения x′ = f(t, x) тождественно равно нулю, если φ(0) = 0.

1.1.12.12. Пусть функция f: R×R → R не возрастает по второму аргументу при любом значении первого. Докажите, что если решения φ и ψ уравнения x′ = f(t, x) совпадают в какой-либо точке t₀, то они совпадают при всех t ≥ t₀, при которых они определены.

1.1.12.13. Докажите, что любое решение скалярного дифференциального уравнения x′ = f(x) монотонно в нестрогом смысле.

1.1.12.14. Пусть функция f: R → R непрерывна и пусть уравнение x′ = f(x) имеет определенное на всей оси решение φ такое, что φ(t) → x₀ при t → + ∞. Докажите, что функция ψ(t) ≡ x₀ является решением этого уравнения.

1.1.12.15. Покажите, что любые три непрерывно дифференцируемые на R функции φ₁, φ₂, φ₃, связанные при всех t соотношениями φ₁(t) < φ₂(t) < φ₃(t), являются решениями некоторого уравнения Риккати

x′ = p(t)x2 + q(t)x + r(t)

с непрерывными коэффициентами p, q, r.

1.1.12.16. Пусть φ — периодическое решение уравнения Риккати вида

x′ = x2 + q(t)x + r(t).

Докажите, что найдутся числа t_i (i = 1, 2) и вещественные корни λ_i уравнения λ² + q(t_i)λ + r(t_i) = 0 такие, что λ₁ ≤ φ(t) ≤ λ₂ при всех t ∈ R.

1.1.12.17. Покажите, что если уравнения x′ = f(t, x) и x′ = g(t, x) эквивалентны при t < x + 1 и при t > x¹⁾, то они эквивалентны.

1.1.12.18. Докажите, что если V(x) = x12 + x22 — интеграл двумерной системы x′ = f(t, x), то любое ее решение ограничено.

¹⁾ Имеется в виду эквивалентность этих уравнений, как уравнений с правыми частями, определенными на D(f) = D(g) = {(t, x): t < x + 1}, и уравнений с правыми частями, определенными на D(f) = D(g) = {(t, x): t > x}.

File based on translation from T_EX by T_TH, version 2.32.
Created 31 Dec 2001, 12:27.
Last modified 8 Apr 2002.