§ 4.2. Основные понятия теории устойчивости

В этом параграфе формулируются и обсуждаются определения разных видов устойчивости.

4.2.1. Пример. Общее решение уравнения

x′ = ax,

(1)

как известно, задается формулой

Ceat   (C ∈ R).

Среди его решений выделим одно:

x = 0

и поставим вопрос о его устойчивости, т. е. о том, приводят ли малые отклонения от него при t = 0 к малым же отклонениям при всех t ≥ 0? Ответ будет различным в зависимости от знака a. При a < 0 нулевое решение устойчиво асимптотически, т. е. малым отклонениям от него в момент t = 0 соответствуют отклонения при t ≥ 0 не только малые, но и асимптотически стремящиеся к нулю (см. рис. 1). При a = 0 оно устойчиво — малым отклонениям в нулевой момент соответствуют малые отклонения при t ≥ 0. Наконец, при a > 0 нулевое решение неустойчиво, т. е. сколь угодно малые отклонения от него при t = 0 могут приводить к большим отклонениям при t > 0.

Рис. 1.

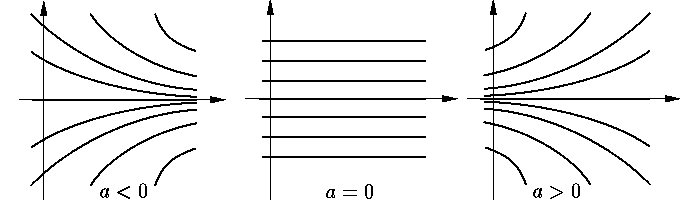
4.2.2. Определения устойчивости. Рассматривается уравнение

x′ = f(t, x),

(НС)

f: [t0, +∞) × Rn → Rn,

(2)

и фиксированное его решение x = φ(t) = gt0t(x0) на [t0, +∞). Предполагается, что выполнены условия обобщенной теоремы Коши — Пикара.

Решение φ называется

— устойчивым по Ляпунову, если (см. рис. 2а)

∀ (ε > 0) ∃ (δ > 0) ∀(x0: |x0 – x0| < δ) ∀ (t ≥ t0) [ | gt0t(x0)– gt0t(x0) | < ε ] ;

— асимптотически устойчивым, если (см. рис. 2б)

1) оно устойчиво,

2) ∃ (Δ > 0) ∀ (x0: |x0 – x0| < Δ) [gt0t(x0)– gt0t(x0)→ 0 при t → +∞];

— асимптотически устойчивым в целом, если оно асимптотически устойчиво, причем в 2) можно взять Δ = +∞; другими словами, 2) заменяется на

2') ∀ (x0) [gt0t(x0)– gt0t(x0)→ 0 при t →+∞];

— экспоненциально устойчивым, если

∃ (Δ1 > 0, M > 0, γ > 0) ∀(x0: |x0 – x0| < Δ1) ∀ (t ≥ t0)

[ | gt0t(x0)– gt0t(x0) | ≤ Me–γ(t– t0) |x0 – x0| ] ;

— экспоненциально устойчивым в целом, если в качестве Δ₁ можно взять +∞, т. е.

∃ (M > 0, γ > 0) ∀ (x0) ∀ (t ≥ t0) [ | gt0t(x0)– gt0t(x0) | ≤ Me–γ(t– t0) |x0 – x0| ] .

Рис. 2.

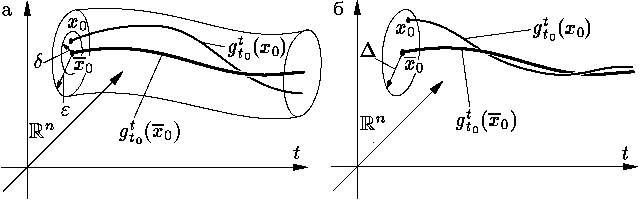
Очевидно, экспоненциальная устойчивость решения влечет его асимптотическую устойчивость, которая, в свою очередь, влечет устойчивость. Нетрудно проверить также, что обратные импликации не справедливы (для второй это уже показано в п. 4.2.1).

Как видно из определения, устойчивость решения φ(t) = gt0t(x0)— это непрерывность семейства операторов сдвига {gt0t: t ≥ t0} в точке x0, равномерная относительно t ∈ [t0, +∞). Из теоремы об условии Липшица для оператора сдвига вытекает, что соответствующее семейство {gt0t: t ∈ [t0, t1]} для любого отрезка [t0, t1] в условиях обобщенной теоремы Коши — Пикара всегда равномерно непрерывно в любой точке x0, т. к.

| gt0t(x0)– gt0t(x0) | ≤ ( exp ∫ t t0 M(s) ds ) ·|x0 – x0|.

В частности, так будет для уравнения (1) и при a > 0, хотя устойчивости нулевого решения нет.

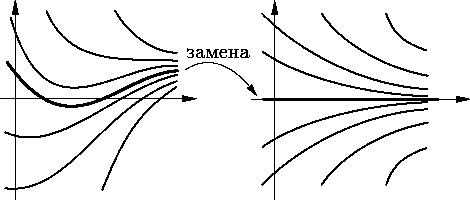
4.2.3. Приведенная система. Произведем в (НС) замену переменных

y = x – φ(t).

(3)

Тогда

y′ = x′ – φ′(t) = f(t, x) – f[t, φ(t)] = f[t, y + φ(t)] – f[t, φ(t)].

Обозначим f[t, y + φ(t)] – f[t, φ(t)] через F(t, y). Таким образом, с учетом (3) (НС) эквивалентна следующей

y′ = F(t, y)

(4)

(см. рис. 3). По отношению к (НС) и заданному ее решению x = φ(t) система (4) называется приведенной, или системой уравнений возмущенного движения. Поскольку

x = φ(t) ⇔ y = 0,

и

|x(t) – φ(t)| = |y(t)|,

справедливо следующее утверждение о приведенной системе: решение φ (НС) обладает одним из свойств устойчивости, если и только если соответствующим свойством обладает нулевое решение приведенной системы.

Рис. 3.

4.2.4. Контрольные вопросы

4.2.4.1. Сформулируйте на языке "ε – δ" определение решения, не являющегося устойчивым по Ляпунову (неустойчивого решения).

4.2.4.2. Приведите пример асимптотически, но не экспоненциально устойчивого решения дифференциального уравнения.

4.2.4.3. Приведите пример устойчивого по Ляпунову, но не асимптотически устойчивого решения дифференциального уравнения.

4.2.4.4. Может ли автономное уравнение x′ = f(x) иметь асимптотически устойчивое непостоянное периодическое решение?

4.2.4.5. Проведите доказательство утверждения о приведенной системе.

4.2.4.6. Выпишите приведенную систему, отвечающую решению φ(t) = sin t уравнения x′′ + x + x² = sin²t.

4.2.5. Задачи

4.2.5.1. Исследуйте устойчивость решений уравнения

x′ = –x(1 – x).

4.2.5.2. Исследуйте устойчивость решений уравнения

x′′ + λx = 0

(λ ∈ R).

4.2.5.3. Приведите пример (НС), нулевое решение которого устойчиво, а все остальные решения неустойчивы.

4.2.5.4. Приведите пример двумерного автономного дифференциального уравнения x′ = f(x) (f(0) = 0) такого, что любое его решение стремится к нулю при t → +∞, а нулевое решение при этом не является устойчивым по Ляпунову.

4.2.5.5. Докажите, что пример из предыдущей задачи нельзя построить в случае скалярного дифференциального уравнения.

4.2.5.6. Покажите, что если в условиях теоремы Коши — Пикара все определенные на [0, +∞) решения (НС) асимптотически устойчивы, то любое решение асимптотически устойчиво в целом.

4.2.5.7. Пусть в (НС) f(t, 0) ≡ 0 и (НС) имеет неограниченное на [0, +∞) решение. Докажите, что это уравнение имеет неустойчивое решение.

4.2.5.8. Пусть правая часть (НС) непрерывна на R×Rⁿ и однородна по x: f(t, λx) ≡ λf(t, x). Докажите, что для устойчивости нулевого решения необходимо и достаточно, чтобы семейство решений, выходящих из точек единичного шара с центром в нуле в нулевой момент времени, было равномерно ограничено на [0, +∞).

4.2.5.9. Пусть правая часть (НС) удовлетворяет условиям теоремы Коши — Пикара и f(t, 0) ≡ 0. Может ли нулевое решение этого уравнения быть устойчивым относительно начального момента t₀ и не быть устойчивым относительно начального момента t₁ ≠ t₀?

4.2.5.10. Пусть правая часть (НС) удовлетворяет условиям теоремы Коши — Пикара и T-периодична по t: f(t + T, x) ≡ f(t, x). Пусть G = g0T— оператор сдвига за период. Докажите, что если G — сжимающий оператор (т. е. ||G(x) – G(y)|| ≤ k||x – y|| при некотором k < 1 и всех x, y), то любое решение этого уравнения асимптотически устойчиво в целом, а если G — нерастягивающий оператор (т. е. ||G(x) – G(y)|| ≤ ||x – y|| при всех x, y), то любое решение этого уравнения устойчиво по Ляпунову.

File based on translation from T_EX by T_TH, version 2.32.
Created 19 Jan 2002, 23:59.
Last modified 18 Apr 2002.