§ О11. Динамические системы

Простейшие свойства автономных (или, как их часто называют, динамических) систем дифференциальных уравнений были нами установлены в п. 2.5.3. В этом очерке мы продолжим изучение специфических свойств автономных систем уравнений

x′ = f(x),

(1)

отличающих такие системы от неавтономных.

Предполагается, что Rn → Rn и удовлетворяет условию Липшица; поэтому решение задачи Коши для уравнения (1) с любыми начальными данными определено на всей оси и единственно. Через gts мы будем как всегда обозначать оператор сдвига по траекториям уравнения (1), а через gt — поток, порожденный этим уравнением, т. е. семейство отображений {gt} = {g0t}. Известно, что

gt = gst+s

при всех s ∈ R. В терминах решений уравнения (1) этот факт эквивалентен тому, что сдвиг вдоль оси t любого решения уравнения (1) является его решением.

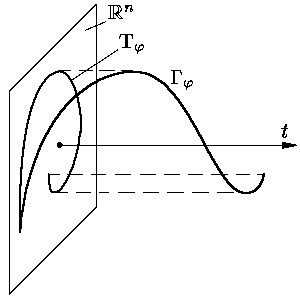
Напомним, что интегральной кривой уравнения (1) мы называем график Γ_φ любого решения φ в расширенном фазовом пространстве R×Rⁿ, а траекторией T_φ — проекцию интегральной кривой на фазовое пространство Rⁿ (см. рис. 1). Таким образом, если φ — определенное на D(φ) решение уравнения (1), то по определению

Γφ = {(t, x) ∈ R×Rn: t ∈ D(φ), x = φ(t)},

Tφ = {x ∈ Rn: x = φ(t), t ∈ D(φ)},

Рис. 1.

Задача О11.1. Докажите,что если две траектории отвечают непродолжимым решениям уравнения (1) и имеют общую точку, то они совпадают.

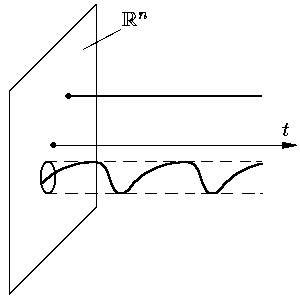
В дальнейшем мы под траекториями будем понимать только траектории отвечающие максимальным (непродолжимым) решениям системы (1).

Траекторию, соответствующую стационарному (т. е. постоянному) решению, будем называть стационарной точкой (положением равновесия), а траекторию, соответствующую периодическому решению — циклом. Если найдется такое число T > 0, что φ(t₁) ≠ φ(t₂) при 0 < |t₁ – t₂| < T и φ является T-периодическим решением, то о траектории T_φ будем говорить как о цикле без самопересечений (см. рис. 2). Ясно, что если T-периодическое решение φ порождает цикл без самопересечений, то решение φ, рассматриваемое как 2T-периодическое, порождает цикл с самопересечениями; поэтому понятие цикла без самопересечений является характеристикой не только самой траектории, но и порождающего ее решения. Наконец, мы будем говорить, что траектория T_φ не имеет самопересечений, если φ(t₁) ≠ φ(t₂) при любых неравных t₁ и t₂.

Рис. 2.

Имеет место следующая

Теорема о типах траекторий автономных систем. Каждая траектория системы (1) является либо стационарной точкой, либо циклом без самопересечений, либо траекторией без самопересечений.

Д о к а з а т е л ь с т в о.  Пусть T_φ — отвечающая максимальному решению φ траектория системы (1). Если T_φ имеет самопересечение, т. е. существуют такие τ и θ, что θ > τ и φ(τ) = φ(θ), то решение φ является (θ – τ)-периодическим. Действительно,

φ(t) = gτt[φ(τ)]= gθt+θ–τ[φ(τ)] = gθt+θ–τ[φ(θ)] = φ[t + (θ – τ)]

при всех t ∈ R. Далее в доказательстве нам потребуются следующие утверждения.

Задача О11.2. Пусть φ — непрерывная функция на R. Тогда множество всех ее периодов: а) образует аддитивную группу, б) является замкнутым.

Обозначим через T точную нижнюю грань множества положительных периодов решения φ. Альтернатива такова: либо T > 0, либо T = 0. В первом случае, как нетрудно видеть, траектория образует цикл без самопересечений (периода T). Покажем, что во втором случае T_φ есть стационарная точка. Поскольку T = 0, множество P периодов решения φ содержит сколь угодно малые числа. Поэтому, так как P — аддитивная группа, P всюду плотно на числовой прямой, а так как P замкнуто, P = R. Таким образом, любое вещественное число является периодом решения φ, что очевидно эквивалентно его стационарности.

Задача О11.3. Приведите пример неавтономной системы, имеющей непериодическое решение, траектория которого имеет самопересечения, и пример автономной системы (правая часть которой по необходимости не удовлетворяет условию Липшица), имеющей периодическое решение минимального положительного периода T, порождающее цикл с самопересечением.

Задача О11.4. Докажите, что в одномерном случае траекториями автономной системы могут быть только множества вида: точка, открытый промежуток, открытый луч, вся прямая.

Теперь мы переходим к исследованию поведения решений при t → ∞. Пусть φ — решение уравнения (1), определенное на всей оси. Частичные пределы φ при t → +∞ называются ω-предельными точками траектории T_φ (и решения φ). Множество всех ω-предельных точек траектории T_φ называется ω-предельным множеством этой траектории и обозначается через Ω(T_φ). Другими словами, точка x лежит в Ω(T_φ) в том и только том случае, когда существует такая последовательность t_k → +∞, что lim_k→∞φ(t_k) = x. Аналогичная конструкция при t → –∞ приводит к понятию α-предельной точки и α-предельного множества A(T_φ) траектории T_φ (см. рис. 3).

Рис. 3.

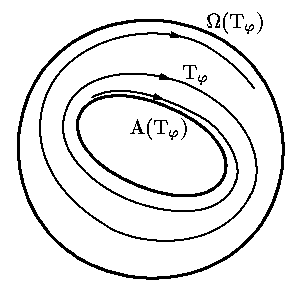
Задача О11.5. Покажите,что

Ω(Tφ) = ∩ t ∈R φ([t,+∞)) ,    A(Tφ) = ∩ t ∈R φ((–∞,t]) ,

где черта означает замыкание множества в Rⁿ.

Структуру ω-предельных множеств частично выясняет следующая

Теорема о структуре ω-предельных множеств. Для любого решения φ системы (1) множество Ω(T_φ) замкнуто. Если, кроме того, решение φ ограничено вправо, т. е. множество φ([0, +∞)) ограничено, то Ω(T_φ) непусто, компактно и связно.

Д о к а з а т е л ь с т в о.  Замкнутость Ω(T_φ) очевидна в силу задачи О11.5. Непустота вытекает из относительной компактности ограниченных подмножеств конечномерного пространства, а компактность Ω(T_φ) — из только что упомянутого факта и замкнутости ω-предельного множества.

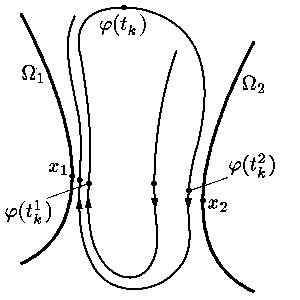
Для доказательства связности Ω(T_φ) предположим противное. Тогда, по определению, Ω(T_φ) представимо в виде объединения двух замкнутых непересекающихся подмножеств Ω₁ и Ω₂. Расстояние

ρ = inf{||x – y||: x ∈ Ω1, y ∈ Ω2}

в силу замкнутости и ограниченности Ω1 и Ω2 положительно. Пусть xi ∈ Ωi (i = 1, 2) — произвольные точки. По определению Ω(Tφ) найдутся такие tk1, tk2 → +∞, что

φ(tk1)→ x1 ∈ Ω1 и φ(tk2)→ x2 ∈ Ω2 при k → ∞.

Не теряя общности, можно считать, что при всех k ∈ N₊

tk1< tk2< t1k+1

и

inf{||φ(t1k)– x ||: x ∈ Ω1} < ρ/2,    inf{||φ(t2k)– x ||: x ∈ Ω2} < ρ/2.

В силу непрерывности φ и замкнутости и ограниченности Ω1 и Ω2 найдутся такие tk ∈ (t1k, t2k), что

inf{||φ(tk) – x||: x ∈ Ω1} ≥ ρ/2, inf{||φ(tk) – x||: x ∈ Ω2} ≥ ρ/2

(2)

(см. рис. 4). Поскольку последовательность φ(tk) ограничена (и следовательно, относительно компактна), некоторая ее подпоследовательность φ(tkm) сходится, скажем, к точке z (ω-предельной точке траектории Tφ). Заменяя в (2) k на km и переходя к переделу при m → ∞, получим противоречие: z ∉ Ω1∪ Ω2 = Ω(Tφ).

Аналогичная теорема имеет место и для α-предельных множеств.

Рис. 4.

Множество M ⊆ Rⁿ называется положительно (соответственно, отрицательно) инвариантным множеством уравнения (1) (и порожденного им потока g^t), если g^t(M) ⊆ M при всех t > 0 (соответственно, t < 0). Одновременно положительно и отрицательно инвариантное множество называется инвариантным.

Задача О11.6. Докажите, что объединение любого семейства траекторий является инвариантным множеством. Наоборот, любое инвариантное множество есть объединение некоторого семейства траекторий.

Теорема об инвариантности предельных множеств. ω- и α-предельные множества любой траектории инвариантны.

Д о к а з а т е л ь с т в о.  Пусть x ∈ Ω(T_φ), т. е. существует такая последовательность t_k → ∞, что lim_k→∞φ(t_k) = x. Тогда при любом t ∈ R в силу непрерывности оператора сдвига

gt(x) = gt ( lim k→∞  φ(tk) ) = lim k→∞ gt[φ(tk)] = lim k→∞ φ(tk + t) ∈ Ω(Tφ),

что и требовалось доказать.

Таким образом, предельные множества любой траектории состоят из траекторий системы (1).

Продолжая изучение поведения решений при t → ∞, перейдем к исследованию устойчивости решений и траекторий динамических систем. Начнем с одного наводящего примера. Рассмотрим автономную систему, фазовый портрет которой изображен на рис. 5, причем, пусть время обращения фазовой точки по круговым траекториям зависит от радиуса этой траектории. Похожий фазовый портрет имеет, например, уравнение математического маятника y′′ + ω²sin y = 0 в окрестности нижнего положения равновесия. Выберем произвольную траекторию (отличную от стационарной точки) и порождающее ее решение φ. Заметим теперь, что это решение не является устойчивым по Ляпунову. Действительно, как бы близко к φ(0) мы не взяли начальные данные решения ψ (отличного от φ), при некоторых t > 0 в силу различия периодов решений φ и ψ точки φ(t) и ψ(t) будут почти диаметрально противоположными и, как следствие, расстояние между φ(t) и ψ(t) не может быть сделано сколь угодно малым. Положение же равновесия этой динамической системы очевидно устойчиво по Ляпунову.

Рис. 5.

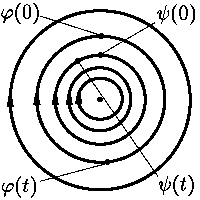
С асимптотической устойчивостью дело обстоит еще хуже, а именно, всякое периодическое нестационарное решение φ автономной системы никогда(!) не бывает асимптотически устойчивым. В самом деле, начальные данные решений φ(t) и ψ(t) = φ(t + τ) при малых τ сколь угодно близки, а функция α(t) = ||φ(t) – ψ(t)|| не может стремиться к нулю при t → ∞, т. к. α является периодической ненулевой функцией.

В то же время, представляется физически естественным считать колебания математического маятника вблизи нижнего состояния равновесия устойчивыми: малые возмущения начальных данных приводят к малым изменениям амплитуды, фазы и частоты колебаний. В этом направлении мы и модифицируем понятия устойчивости и асимптотической устойчивости.

Полутраекторией Tφ+, порожденной решением φ, будем называть часть траектории Tφ, отвечающую положительным значениям t. Решение φ системы (1) и соответствующую ему траекторию Tφ называют орбитально устойчивыми, если для каждого ε > 0 найдется такое положительное δ, что из неравенства ||φ(0) – x || ≤ δ вытекает неравенство

inf{||gt(x) – y ||: y ∈ T+φ}≤ ε

(3)

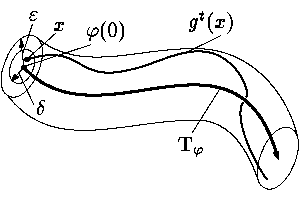
при всех t ≥ 0. Соотношение (3) означает, что при малых возмущениях начальных данных траектория решения остается в ε-окрестности полутраектории Tφ+ (см. рис. 6). Таким образом, требование ||gt(x) – φ(t)|| ≤ ε в определении устойчивости по Ляпунову заменяется более слабым требованием (3).

Рис. 6.

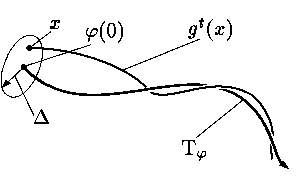
Орбитально устойчивое решение φ и соответствующая траектория Tφ называются орбитально асимптотически устойчивыми, если найдется такое Δ > 0, что inf{||gt(x) – y||: y ∈ Tφ+}→ 0 при k → ∞ как только inf{||x – y||: y ∈ Tφ+} ≤ Δ. Другими словами, расстояние от gtx до полутраектории Tφ+ стремится к нулю при t → ∞, если решение gtx начинается достаточно близко к Tφ+ (см. рис. 7).

Рис. 7.

Предельным циклом называют цикл T_φ, для которого либо T_φ = Ω(T_φ), либо T_φ = A(T_φ).

Задача О11.7. Является ли цикл {(x1, x2) ∈ R2: x21+ x22= 1} системы

x′1= – x2 + x1(1 – x21 – x22),

x′2= x1 + x2(1 – x21 – x22)

предельным? Орбитально асимптотически устойчивым?

При исследовании устойчивости предельных циклов весьма полезным оказывается рассмотрение так называемой функции последования. Строится она следующим образом. Пусть Tφ — предельный цикл системы (1). Тогда f(x) ≠ 0 при всех x ∈ Tφ (почему?). Зафиксируем точку x0 ∈ Tφ и обозначим через E (n – 1)-мерную гиперплоскость, проходящую через точку x0 и ортогональную вектору f(x0) (см. рис. 8). Будем считать, что E наделена аффинной структурой, индуцированной из Rn, и кроме того, будем считать, что начало координат в E фиксировано в точке x0. Наконец, будем считать E нормированным пространством с нормой опять же индуцированной из Rn. Пусть U — малая окрестность нуля в E. Для точки x ∈ U обозначим через G(x) первую точку пересечения кривой t → gt(x) (t > 0) с гиперплоскостью E, т. е. такую точку y ∈ E, что y = gt0(x) при некотором t0 > 0, причем t0 таково, что gt(x) ∉ E при t ∈ (0, t0) (см. рис. 8). Через D(G) обозначим множество тех x ∈ U, для которых G(x) определена. Отображение G: D(G) → E и называется функцией последования или оператором последования Пуанкаре.

Рис. 8.

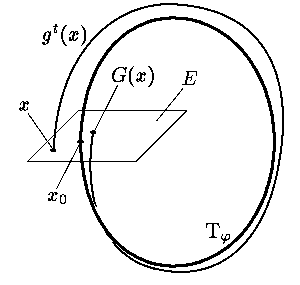
Задача О11.8. Докажите, что G(0) = 0 (здесь 0 — нуль пространства E). Пользуясь теоремой о непрерывной зависимости решений от начальных данных и теоремой о неявной функции, докажите, что в достаточно малой окрестности U нуля в E отображение G определено и непрерывно.

Роль, которую играет функция последования при исследовании орбитальной устойчивости, выясняется в следующем утверждении, доказательство которого мы оставляем читателю в качестве упражнения.

Теорема об орбитальной асимптотической устойчивости. Пусть T_φ — предельный цикл уравнения (1) и G — какая-либо функция последования, отвечающая этому циклу. Допустим, что при некотором натуральном k в окрестности U нуля в E определена k-ая степень G^k функции последования, причем, существует q < 1 такое, что при всех x ∈ U

|| Gk(x)|| ≤ q||x||.

(4)

Тогда цикл T_φ орбитально асимптотически устойчив.

Один достаточный признак асимптотической орбитальной устойчивости предельного цикла дает формулируемая ниже теорема Андронова — Витта. Ее можно рассматривать как аналог теоремы Ляпунова об устойчивости по первому приближению.

Пусть f непрерывно дифференцируема и пусть φ — нестационарное T-периодическое решение системы (1). Наряду с уравнением (1) рассмотрим линеаризованное вдоль решения φ уравнение

x′ = A(t)x,

(5)

где A(t) = df/dx|_x=φ(t). Очевидно матрица A является T-периодической и поэтому, в частности, система (5) является правильной по Ляпунову. К сожалению, в случае нестационарного решения φ условия теоремы Ляпунова об устойчивости по первому приближению никогда не бывают выполненными. Действительно, как показывает дифференцирование тождества φ′(t) ≡ f[φ(t)] по t, (ненулевая) периодическая функция ψ(t) = φ′(t) является решением линеаризованного уравнения (5). Поэтому нулевое решение этого уравнения не является асимптотически устойчивым и, следовательно, спектр системы (5) содержит нулевой характеристический показатель.

Тем не менее, удается указать условия, при которых решение φ будет орбитально асимптотически устойчивым. Точнее, имеет место

Теорема Андронова — Витта. Пусть нулевой характеристический показатель линеаризованной системы (5) однократен, а остальные характеристические показатели этой системы отрицательны. Тогда решение φ орбитально асимптотически устойчиво. Более того, для любого решения ψ, начинающегося достаточно близко к траектории T_φ, найдется число τ (называемое асимптотической фазой решения ψ) такое, что ||ψ(t + τ) – φ(t)|| → 0 при t → ∞.

Доказательство этой теоремы мы опускаем. По поводу проверки условия отрицательности характеристических показателей сошлемся на задачу О21.14, в которой описывается спектр характеристических показателей линейной системы с периодическими коэффициентами в терминах ее оператора сдвига за период.

Наконец, заметим, что наличие асимптотической фазы означает, что при t → +∞ решения "наматываются" на предельный цикл T_φ как спирали.

Литературные указания. Термин "динамическая система", в некотором смысле, является синонимом термина "дифференциальное уравнение". Поэтому список литературы к данному очерку весьма обширен. Мы перечислим здесь лишь классические учебники [Арнольд, Бибиков, Коддингтон — Левинсон, Немыцкий — Степанов, Петровский, Понтрягин, Рейссиг — Сансоне — Конти, Хартман, Bhatia — Szegö].

Задачи. О11.9. Приведите примеры динамических систем и их траекторий T_φ таких, что Ω(T_φ) является: а) пустым; б) некомпактным; в) несвязным.

О11.10. Приведите пример динамической системы в R³ и ее траектории T_φ такой, что Ω(T_φ) является тором.

О11.11. Докажите, что если φ ограничено вправо, то

inf{||φ(t) – x||: x ∈ Ω(T)} → 0 при t → ∞.

(6)

Приведите пример автономной системы и ее траектории T_φ, для которой (6) не выполнено.

О11.12. Докажите, что замыкание и внутренность инвариантного множества являются инвариантными множествами.

О11.13. Докажите, что решение φ системы (1) периодично в том и только том случае, если T_φ = Ω(T_φ) (или T_φ = A(T_φ)).

О11.14. Замкнутое непустое инвариантное множество системы (1) называется минимальным, если оно не имеет собственных инвариантных подмножеств системы (1). Приведите пример автономной системы и ее траектории, ω-предельное множество которой не минимально. Докажите, что любой цикл является минимальным инвариантным множеством.

О11.15. Пусть T_φ — траектория системы (1). Докажите, что если Ω(T_φ) = A(T_φ) = ∅, то T_φ — минимальное инвариантное множество.

О11.16. Докажите, что множество M ⊆ Rⁿ является инвариантным в том и только том случае, если вместе с каждой своей точкой оно содержит замыкание траектории, проходящей через эту точку.

О11.17. Докажите, что если ω-предельное множество Ω(T_φ) траектории T_φ системы (1) неограничено, то оно не может иметь ограниченной связной компоненты.

О11.18. Пусть T+φ — положительная полутраектория решения φ автономной системы (1). Продолжением Π+φ траектории Tφ называется множество тех точек x ∈ Rn, для которых найдутся последовательности xk → φ(0) при k → ∞ и tk ≥ 0 такие, что gtk xk → x при k → ∞. Докажите, что продолжение любой траектории положительно инвариантно. Докажите, что

Πφ+ = ∩ r > 0 ∪ gt(B(φ(0), r) t ≥ 0 .

О11.19. Приведите пример траектории Tφ автономной системы, для которой: а) Πφ+= Tφ ∪ Ω(Tφ); б) Πφ+= Tφ ∪ A(Tφ).

Теорема Брауэра гласит: любое непрерывное отображение шара конечномерного пространства в себя имеет неподвижную точку.

О11.20. С помощью теоремы Брауэра докажите, что если система (1) имеет инвариантное множество гомеоморфное шару, то она имеет стационарную точку.

File based on translation from T_EX by T_TH, version 2.32.
Created 19 Jan 2000, 18:34.
Last modified 25 Apr 2002.