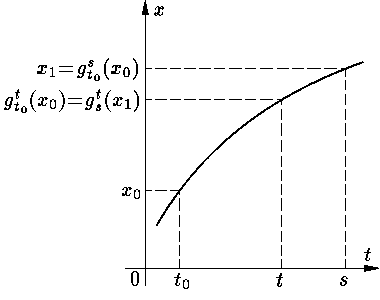§ 2.5. Оператор сдвига

Понятие "оператор сдвига по траекториям дифференциального уравнения" близко к понятию общего решения. Ни то, ни другое обычно не выражается явной формулой, однако многие свойства оператора сдвига можно вывести непосредственно из свойств правой части (НС). Такой подход будет развиваться далее в третьей и четвертой главах, здесь мы рассмотрим лишь простейшие свойства оператора сдвига. Термин "оператор сдвига" не является общепринятым; в том же смысле употребляется термин "отображение за время от t₀ до t" и некоторые другие. Кроме того, в функциональном анализе оператором сдвига называют также не имеющее прямого отношения к дифференциальным уравнениям преобразование функции x(t) в функцию x(t + τ).

2.5.1. Определение оператора сдвига. Рассмотрим задачу Коши

x′ = f(t, x),

(НС)

x(t0) = x0

(НУ)

и предположим, что выполнены условия обобщенной теоремы Коши — Пикара 2.4.1. Для решения этой задачи, которое существует на J и единственно в силу названной теоремы, бывает удобно использовать обозначение gt0t(x0), отражающее зависимость не только от t, но также от t0 и x0. Если t и t0 фиксировать, а x0, менять, то получится отображение gt0t: Rn → Rn, называемое оператором сдвига за время от t0 до t по траекториям уравнения (НС).

Итак, по определению, оператор сдвига gt0t сопоставляет значению решения уравнения (НС) в момент времени t0 значение этого же решения в момент времени t.

В силу обобщенной теоремы Коши — Пикара это определение корректно: каждому x₀ ∈ Rⁿ сопоставляется один и только один x ∈ Rⁿ.

П р и м е р.  Для линейного уравнения

x′ = a(t)x + b(t)

оператор сдвига задается формулой

gt0t(x0) = exp ( ∫ t t0 a(s) ds ) · x0 + ∫ t t0 [ ∫ t s a(σ) dσ ) ] b(s) ds

(1)

(см. п. 1.4.3).

Геометрическая интерпретация оператора сдвига изображена на рис. 1).

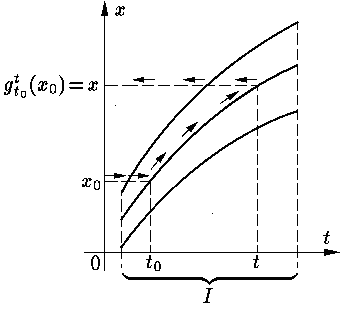
Рис. 1.

2.5.2. Простейшие свойства оператора сдвига.

а) gt0t0= I;

б) (d/dt)gt0t(x0)= f[t, gt0t(x0)];

в) gts· gt0s= gt0t;

г) gt0t взаимно однозначно отображает Rn на Rn и (gt0t)–1= gt0t.

Д о к а з а т е л ь с т в о.  Свойства а) и б) непосредственно следуют из определения gt0t. Для доказательства в) достаточно убедиться, что справедливо тождество

gst[gt0s(x0)]≡ gt0t(x0).

Если левую и правую его части рассматривать как функции от t, то, по определению, это решения уравнения (НС). В точке t = s они совпадают

gss[gt0s(x0)]≡ gt0s(x0).

следовательно, они совпадают всюду (см. рис. 2).

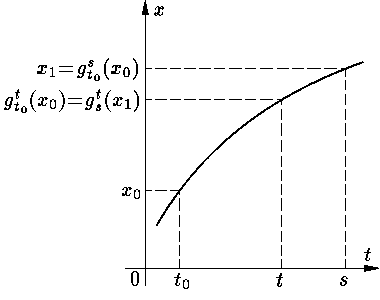
Рис. 2.

Докажем г). Во-первых, D(gt0t)= Rn, т. к. задача Коши имеет решение на J при любом начальном значении x0 ∈ Rn. Аналогично, D(gt0t)= Rn. Наконец, gt0t= (gt0t)–1, т. к.

gt0t· gt0t= I  и  gt0t· gt0t= I

(в частности, это означает, что gt0t взаимно однозначно отображает Rn на Rn).

2.5.3. Оператор сдвига для автономного уравнения. Пусть рассматриваемое уравнение автономно, т. е. его правая часть не зависит от t:

x′ = f(x).

(НАС)

Тогда оператор сдвига обладает дополнительным свойством инвариантности относительно сдвигов вдоль оси t:

д) gt0t+τ·gt+τt0+τ = gtt0.

Д о к а з а т е л ь с т в о.  Покажем, что для (НАС) функция   y(t) = gt+τt0+τ(x0) также является решением. Действительно,

y′(t) = d ds gst0+τ(x0) | s = t+τ · d(t + τ) dt = f[gt+τt0+τ(x0)] = f[y(t)].

Остается заметить, что решения gt+τt0+τ(x0) и gt0t(x0) при t = t0 принимают одно и то же значение x0.

В силу доказанного утверждения для автономного уравнения справедливо, в частности (при τ = –t0), равенство gt0t= g0t–t0. Последнее выражение мы будем обозначать просто gt–t0:

gt–t0 = g0t–t0.

С использованием этого обозначения свойства а) – г) для автономного уравнения можно записать в виде:

а') g⁰ = I;

б') (d/dt)g^t(x₀) = f[g^t(x₀)];

в') g^t · g^s = g^t+s (поскольку очевидно, g₀^t · g₀^s = g_s^t+s · g₀^s = g₀^t+s);

г') (g^t)^–1 = g^–t.

Свойства а'), в') и г') говорят о том, что отображение t → g^s есть гомоморфизм аддитивной группы вещественных чисел на группу взаимнооднозначных отображений Rⁿ на себя (групповая операция — композиция). Семейство {g^t: t ∈ Rⁿ} называют группой операторов, операторов а семейство {g^t: t ∈ [0, +∞)} — полугруппой операторов, порожденной уравнением (НАС).

2.5.4. Примеры. Для операторов сдвига (1) по траекториям линейного однородного уравнения групповое свойство в) означает, что справедливо тождество

[ Φt0(s)x0 + Φt0(s) ∫ s t0 Φ –1 t0 (σ)b(σ) dσ ] Φs(t) + Φs(t) ∫ t s Φs–1(σ)b(σ) dσ =

Φt0(t)x0 + Φt0(s) ∫ t t0 Φs–1(σ)b(σ) dσ =

Это тождество легко проверить непосредственно, если учесть, что

Φs(t)Φt0(s) = Φt0(t)  и   Φs–1(σ) = Φσ(s).

Для автономного линейного уравнения

x′ = ax + b

оператор сдвига за время от t₀ до t имеет вид

gt0t(x0) = ea(t–t0)x0 + ∫ s t0 ea(t – s)b ds = ea(t–t0) ( x0 + b a )   –   b a   =g0t–t0x0.

Следовательно,

gt(x0) = et ( x0  +   b a )   –   b a .

Групповое свойство в') означает, что

et ( [ es ( x0  +   b a )   –   b a ]   +   b a )   –   b a  = et+s ( x0  +   b a )   –   b a .

Очевидно, это верное равенство.

2.5.5. Замечание о качественной теории дифференциальных уравнений. Как следует из определения оператора сдвига по траекториям дифференциального уравнения (НС), задача о нахождении всех решений этого уравнения эквивалентна задаче о нахождении оператора сдвига. Выписать в явном виде оператор сдвига (т. е. найти все решения уравнения) в общем случае невозможно. Кроме того, формулы, задающие явный вид оператора gt0t (в тех случаях, когда это возможно), оказываются зачастую громоздкими и не позволяют извлечь полезную информацию о поведении решений. В силу этих соображений необходимо и полезно изучать свойства оператора сдвига gt0t по свойствам правой части уравнения. Такое изучение носит название качественной теории дифференциальных уравнений. В следующих главах мы будем искать условия на функцию f, при которых отображение (t, t0, x0) → gt0t(x0) непрерывно или дифференцируемо по тем или иным аргументам. Во второй части книги мы будем также изучать более общие нежели условия теоремы Коши — Пикара условия существования оператора сдвига. Отдельную главу качественной теории дифференциальных уравнений составляет так называемая теория устойчивости — теория, изучающая условия равномерной по t ∈ [t0, +∞) непрерывности оператора сдвига.

2.5.6. Контрольные вопросы

2.5.6.1. Почему перечисленные ниже отображения не могут быть операторами сдвига по траекториям какого-либо уравнения вида (НС)

gt0t(x0)= 2x0,

gt0t(x0)= (1 – t + t0)x0,

gt0t(x0)= et–t0 x0 + (t – t0),

gt0t ( x02 x02 )   =   ( et–t0 x01 ) ?

2.5.6.2. Почему отображение gt0t(x0)= x0exp(t2 – t02) не может быть оператором сдвига по траекториям какого-либо автономного уравнения вида (НАС)?

2.5.6.3. Найдите оператор сдвига по траекториям дифференциального уравнения x′ = tx + 1.

2.5.6.4. Оператором сдвига по траекториям какого уравнения является отображение gt0t(x0)= et–t0x0?

2.5.7. Задачи

2.5.7.1. Найдите операторы сдвига по траекториям систем

x′1 = x2,    x′2 = –x1

и

x′1 = x2,    x′2 = –x1 + sin t.

2.5.7.2. Покажите, что оператор сдвига g0t по траекториям уравнения x′ = x2 не определен на всем пространстве R ни при каких t > 0.

2.5.7.3. Пусть f в (НС) удовлетворяет условиям теоремы Коши — Пикара и T-периодична по T: f(t + T, x) ≡ f(t,x). Докажите, что gt0+Tt+T =  gt0t и, в частности, gt0t0+T =  g0T.

2.5.7.4. В условиях предыдущей задачи покажите, что решение x = φ(t) уравнения (НС) является T-периодическим в том и только том случае, когда φ(0) является неподвижной точкой оператора сдвига за период g0T,т. е. g0Tφ(0)= φ(0).

2.5.7.5. Определим оператор T_h: R×Rⁿ → R×Rⁿ равенством

Th(t, x) = (t + h, x).

Покажите, что Th переводит интегральные кривые (НАС) в интегральные кривые и Th[t, gt0t(x0)]= gt0+ht+h(x0).

2.5.7.6. Покажите, что оператор сдвига gt0t по траекториям уравнения x′ = –x при t > t0 является сжимающим, т. е. удовлетворяет условию Липшица с некоторой константой L < 1, а при t < t0 — растягивающим, т. е.

∃(L > 1) ∀(x0, x1 ∈ R) [||gt0t(x0)– gt0t(x1)||≥ ||x0 – x1||].

File based on translation from T_EX by T_TH, version 2.32.
Created 5 Jan 2002, 13:48.
Last modified 12 Apr 2002.