
|
§ О3. Теоремы о продолжимости решений |

|
Гнаться за невозможным — безумие.
Марк Аврелий. Размышления
Договоримся о терминологии. Пусть φ и
ψ — решения уравнения
(всюду в этом очерке предполагается, что
f: D(f) →
Rn — непрерывное отображение,
D(f) — открытое подмножество
R×Rn).
Если D(φ)
⊆ D(ψ)
и φ(t) ≡
ψ(t) при t ∈
D(φ),
то решение ψ называется
продолжением решения
φ, а φ —
частью решения ψ;
решение φ при этом называется
продолжимым.
Если в этой ситуации
sup D(ψ) >
sup D(φ)
(соответственно,
inf D(ψ) <
inf D(φ)),
то решение φ называется продолжимым вправо
(соответственно, влево). Если единственным продолжением решения
φ является φ,
то оно называется максимальным
или непродолжимым решением.
Нас будут интересовать следующие вопросы. В каких случаях решение
продолжимо? Каков механизм "появления непродолжимости"? Когда
решение можно продолжить до максимального? Наконец, при каких
условиях максимальное решение определено на заданном отрезке?
На первый вопрос ответ дает следующая
Теорема о продолжимости решения на точку. Чтобы решение
φ: [a, b] →
Rn уравнения (1) было
продолжимо вправо необходимо и достаточно, чтобы существовал
конечный предел
и точка (b, x0) лежала в D(f).
Необходимость этих условий очевидна в силу определения решения и открытости
D(f). Достаточность же доказывается следующим образом.
Пусть ψ — решение уравнения (1),
удовлетворяющее начальному условию
Это решение по теоремe Пеано
существует в некоторой ε-окрестности
точки b. Нетрудно показать теперь, что функция
~
x
|
(t)= | { |
φ(t), если t ∈
[a, b),
ψ(t), если
t ∈[b, b + ε)
|
|
является продолжением решения φ.
Задача О3.1. Докажите последнее утверждение.
Эта теорема утверждает, что решение φ уравнения
(1) может быть не продолжимо вправо лишь в
трех случаях:
1) предел (2) не существует;
2) limt→b–0φ(t)
= ∞;
3) (b, x0) ∉
D(f), т. е. точка (b, x0)
лежит на границе множества D(f).
Покажем, что первая ситуация может реализоваться лишь в случае,
когда множество {b}×P,
где P — множество частичных пределов функции
φ при t →
b – 0, не пересекается с
D(f).
Для простоты рассмотрим скалярный случай n = 1.
Итак, пусть ({b}×P) ∩
D(f) ≠
∅, а предел (2) не существует, т. е.
| β ≝ |
lim
t → b–0 |
φ(t) ≠ |
lim
t → b–0 |
≝ |
α. |
| (3) |
В силу открытости множества D(f) пересечение
({b}×P) ∩
D(f)
содержит целый отрезок {b}×[α1,
β1] (см. рис. 1).
Из соотношения (3), неравенств α <
α1 <
β1 <
β и второй теоремы Больцано — Коши (о
промежуточных значениях непрерывной функции) следует существование такой последовательности
tk→
b – 0, что
|
t1 < t2 < ...;
φ(t2k) =
β1,
φ(t2k–1) =
α1 (k = 1, 2, ...), |
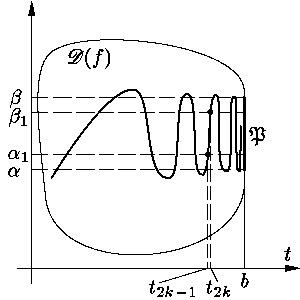
Рис. 1.
причем можно считать, что
|
α1
≤ φ(t)
≤ β1
при t ∈[t2k–1,
t2k]. | (4) |
По теореме Лагранжа при каждом k найдется
τk ∈
(t2k–1, t2k) такое, что
| φ′(τk) = |
φ(t2k) –
φ(t2k–1)
t2k – t2k–1
|
. |
|
В силу (4), не ограничивая общности, можно считать последовательность
{φ(τk)}
сходящейся: limk→∞φ(τk) =
γ, причем, (b, γ)
∈ D(f).
Но тогда, с одной стороны, в силу непрерывности f,
lim
k
→ ∞
|
φ′(τk)
= |
lim
k
→ ∞
|
f[τk,
φ(τk)] =
f(b, γ).
|
|
а с другой —
lim
k
→ ∞
|
φ′(τk)
= |
lim
k
→ ∞
|
β1 –
α1
t2k –
t2k – 1
|
= ∞. |
|
Противоречие.
Задача О3.2. Восстановите детали доказательства.
Задача О3.3. Приведите пример определенной на открытом подмножестве
R×R непрерывной функции f такой, что решением
дифференциального уравнения (1) на интервале (0, 1) является
функция x(t) = sin(1/t).
Из вышесказанного следует, что решение уравнения (1)
не продолжимо за точку лишь в том случае, когда
оно достигает границы области определения правой части уравнения (в случае 2 границей
неограниченного множества можно считать "бесконечность").
Имеет место также следующая
Теорема о продолжимости решения до максимального. Любое
решение уравнения (1) является частью
некоторого максимального решения.
Мы докажем эту теорему при следующем дополнительном предположении: для любой точки
(t0, x0)
∈ D(f)
решение уравнения (1)
единственно в некоторой окрестности точки t0
(существование такого решения вытекает из теоремы
Пеано). В общем случае доказательство сложнее. Итак, пусть
t0 ∈
D(f) и x0 =
φ(t0).
Обозначим через T множество тех τ
∈ R, для которых уравнение (1)
имеет на отрезке [t0, τ]
решение, проходящее через точку (t0, x0).
Обозначим sup T через β,
а inf T — через α и определим на
(α, β)
функцию ψ следующим образом: для любого
t ∈ (α,
β)
где x — определенное на [t0, t]
решение уравнения (1), проходящее через точку
(t0, x0).
Из единственности решения вытекает корректность определения функции
ψ. Легко показывается, что
ψ есть искомое максимальное
продолжение решения φ. Еще раз подчеркнем,
что без предположения единственности доказательство теоремы существенно
менее тривиально (см. задачи 8 – 11 в конце очерка).
Задача О3.4. Пусть D(f) =
[a, b]×Rn,
f непрерывна, t0
∈ (a, b)
и x0 ∈
Rn. Докажите, что если φ —
определенное на (α, β)
максимальное решение уравнения (1),
удовлетворяющее начальному условию x(t0) =
x0, то либо β = b,
либо ||φ(t)||
→ ∞ при t
→ β0.
Особый интерес представляет случай, когда D(f) =
[a, b]×Rn.
В этой ситуации любое решение продолжимо на весь отрезок
[a, b] в том и только том случае, если для
любого решения x уравнения (1), определенного на
[a, b], имеет место оценка
|
||x(t)|| ≤
C, t ∈ [a, b]
| (5) |
(ср. с задачей О3.4); здесь C — некоторая константа,
зависящая, вообще говоря, от решения. Подчеркнем условный характер требования
(5): если x — решение уравнения
(1), то имеет место оценка (5);
при этом ничего не предполагается о существовании решения. Такие условия называются
априорными оценками (название объясняется тем, что
a priori не предполагается существования решения). Они играют важную роль в теории
дифференциальных уравнений.
Один универсальный прием получения априорных оценок описывается в следующей теореме.
Теорема об априорных оценках. Пусть f: [a,
b]×Rn →
Rn непрерывна и существует такая непрерывная функция
L: [a, b]×R
→ R, что, во-первых,
|
|| f(t, x)
|| ≤
L(t, ||x||)
| (6) |
при всех (t, x)
∈ D(f)
и, во-вторых, любое решение уравнения
продолжимо на отрезок [a, b].
Тогда для решений уравнения (1) имеет место априорная
оценка (5) и, следовательно, любое решение уравнения (1)
продолжимо на отрезок [a, b].
Д о к а з а т е л ь с т в о. Итак, пусть x — решение уравнения
(1). Обозначим
||x(t)|| через
φ(t).
Тогда (ср. задачей О2.5
в очерке О2)
|
D*φ(t)
≤
|D*||x(t)|||
≤
||x′(t)||
|
(здесь D* —
нижнее левое производное число
Дини). В силу же условий нашей теоремы
|
||x′(t)|| =
||f[t, x(t)]||
≤ L[t,
||x(t)||] =
L[t, φ(t)]. |
Таким образом,
|
D*φ(t)
≤ L[t, φ(t)],
t ∈ [a, b]. |
Пусть теперь y — верхнее решение
уравнения (7), удовлетворяющее начальному условию
y(a) =
||x(a)||
(по условию оно определено на [a, b] — см.
задачу О2.4
в цит. очерке). В силу теоремы о
нестрогих дифференциальных неравенствах с производными числами
а поскольку y — непрерывная на отрезке функция, найдется такое C, что
Оценка (5) очевидным образом следует из последнего неравенства.
В силу доказанной теоремы для продолжимости всех решений
уравнения (1) достаточно указать оценочную функцию L,
для которой заранее известно, что все решения уравнения (7)
продолжимы на заданный отрезок. Такими функциями могут быть, например,
функции C|y|,
C|y·ln |y||,
C|y(ln |y|)·(ln|ln|y||)|,
... (докажите!).
Задача О3.5. Пусть
f: R×Rn
→ Rn и при всех t, x
| ||f(t,
x)|| ≤
a(t)||x|| +
b(t), |
где a и b — непрерывные на R функции.
Докажите, что любое решение уравнения (1)
продолжимо на всю ось.
Литературные указания. Теоремы о продолжимости решений
см., напр., в [Арнольд,
Бибиков,
Коддингтон — Левинсон,
Немыцкий — Степанов,
Понтрягин,
Хартман,
Hale].
Задачи. О3.6. Докажите, что любое решение уравнения Ван дер Поля
| y′′ +
ε(y2 – 1)y′ +
y = 0 |
(ε > 0) продолжимо
на всю ось.
О3.7. Пусть f ограничена на D(f).
Покажите, что для любого решения φ:
[a, b) → Rn
уравнения (1) предел (2) существует и конечен.
В следующих четырех задачах описываются этапы доказательства
теоремы о продолжимости решения до максимального без
упрощающего предположения о локальной единственности решения.
О3.8. Пусть U — компактное подмножество
D(f), V — открытое содержащее U
множество, замыкание которого лежит в D(f).
Докажите, что найдется T > 0 такое, что при любых
(t0, x0) ∈
U задача Коши
имеет на отрезке [t0 – T,
t0 + T] (см. доказательство
теоремы Пеано).
О3.9. В условиях задачи 8 покажите, что любое решение
φ: (a, b)
→ Rn
уравнения (1) такое, что
(t, φ(t)) ∈
U при t ∈
(a, b), может быть продолжено на отрезок
[c, d] ⊃
(a, b) такой, что (c,
φ(c)) ∉
U и (d, φ(d))
∉ U.
|
О3.10. Пусть Uk
(k = 1, 2, ...) — открытые множества такие, что
Uk компактны,
Uk ⊂
Uk+1 и D(f) =
∪∞k=1Uk
(покажите, что такую последовательность множеств можно построить).
Пусть φ: (a, b) →
Rn — решение уравнения (1)
такое, что (t, φ(t))
∈ U1 при t
∈ (a, b).
Пользуясь результатами предыдущей задачи, докажите, что существует продолжение
ψ: (c, D)
→ Rn
решения φ и последовательности точек
{ck} и {dk}
такие, что (ck,
ψ(ck)),
(dk, ψ(dk))
∈
Uk+1\Uk
при всех k. |
О3.11. Докажите теорему
о продолжимости решения до максимального.
В оставшихся задачах предполагается, что
D(f) =
R×Rn, а функция f непрерывна.
|
О3.12. Пусть в уравнении (1) f
удовлетворяет условию ||f(t,
x)|| ≤
l(t)||x||,
причем ∫∞0l(t) dt<
∞. Тогда все решения уравнения (1)
продолжимы вправо до +∞. |
О3.13. Пусть в
уравнении (1) ||f(t,
x)|| ≤
φ(||x||)
при всех (t, x), причем
φ: R+ →
R+ непрерывна положительна и
Докажите, что любое решение уравнения (1)
продолжимо на всю ось.
О3.14. Пусть в уравнении (1) f удовлетворяет условию
||f(t, x)||
≤
l(t)φ(||x||),
где φ такая же, как в предыдущей задаче, а
Докажите, что любое решение уравнения (1)
продолжимо на всю ось.
О3.15. Пусть в уравнении (1)
(x, f(t, x)) ≤
l(t)||x||2
((·,·) — скалярное произведение
в Rn) при всех t
и достаточно больших ||x||,
причем l — непрерывная функция. Докажите, что любое решение
уравнения (1) неограниченно продолжимо вправо.
О3.16. Пусть V:
R×Rn →
Rn — функция Ляпунова
уравнения (1).
Докажите, что если найдется такая непрерывная функция
W: Rn →
Rn, что W(x) → +∞ при
||x||
→ +∞
и V(t, x) ≥
W(x), то любое решение уравнения (1)
неограниченно продолжимо вправо.




