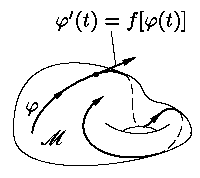|
§ О5. Дифференциальные уравнения на многообразиях |

|
Крива свиль, да столяры хвалят.
Русская пословица
Фазовым пространством математического маятника
является плоскость (x, x′)
и, как мы знаем, фазовый портрет маятника
имеет вид, изображенный на рис. 1.
Поскольку при значениях x, отличающихся на 2πk
(k ∈ N), маятник находится в одном и том же положении,
удобно считать фазовым пространством маятника не плоскость, а цилиндр,
получающийся из плоскости отождествлением точек, абсциссы которых
отличаются на 2πk. Соответствующий фазовый портрет
получается "наматыванием" фазового портрета маятника на плоскости на этот цилиндр
(см. рис. 2).
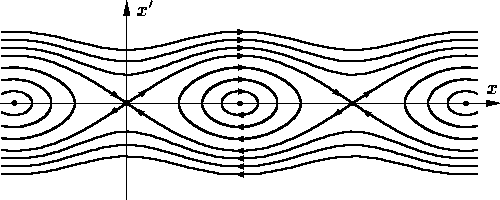
Рис. 1.
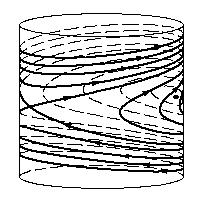
Рис. 2.
В данном очерке мы описываем формальную конструкцию, позволяющую
рассматривать дифференциальные уравнения не только в линейных
конечномерных пространствах, но и на произвольных гладких
конечномерных многообразиях. От читателя требуется владение
понятиями теории многообразия в объеме университетского курса
топологии.
Всюду ниже r — натуральное число,
M —
Cr+1-гладкое
m-мерное многообразие, задаваемое атласом
{Φ}, состоящим из
карт Φ:
U→ Rm
(U ⊆ M),
TM —
касательное расслоение,
TxM —
касательное к M
в точке x ∈ M
пространство, π:
TM →
M — каноническая проекция
TM
на M: π(y) —
это та точка x ∈ M,
в которой y касается M, т. е.
π(y) ∈
TxM.
Если N и K —
Cr-гладкие многообразия и
f: N →
K — Cr-гладкое
отображение, то через df:
TN →
TK
обозначается касательное отображение, df(x):
TxN →
Tf(x)K
при всех x ∈ N.
По определению, Cr-гладкое
отображение f: M →
TM
называется векторным полем на многообразии
M, если
π[f(x)] = x
при всех x ∈
M, т. е.
f(x) ∈
TxM
(см. рис. 3).
(Автономным) дифференциальным уравнением на
многообразии M называется уравнение вида
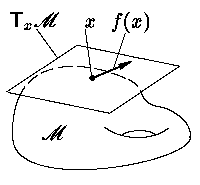
Рис. 3.
Решением уравнения (1)
на интервале J ⊆ R называется
Cr+1-гладкое отображение
φ: J →
M, обращающее уравнение (1)
в тождество на J: φ′(t) ≡
f[φ(t)]
при всех t ∈ J
(см. рис. 4).
Подчеркнем, что φ′(t)
при каждом t есть вектор из
Tφ(t)M
(который и должен совпадать с вектором f[φ(t)]).
Как обычно, образ отображения φ
называется траекторией решения φ.
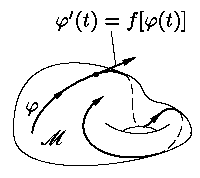
Рис. 4.
Локально дифференциальное уравнение на m-мерном
многообразии ничем не отличается от дифференциального уравнения на
Rm, т. е. системы m
дифференциальных уравнений с m неизвестными.
Смысл этого утверждения таков. Пусть
Φ: U →
Rm — карта на многообразии M,
а φ: J →
U — решение уравнения (1).
Определим на Rm отображение F =
dΦ·f·Φ–1,
т. е. положим F(x) =
dΦ[Φ–1(x)](f[Φ–1(x)])
для всех x ∈
Φ(U), и рассмотрим в
Rm (точнее, в
Φ(U) ⊆
Rm) дифференциальное уравнение
Тогда функция ψ: J →
Rm, задаваемая формулой
ψ(t) =
Φ[φ(t)]
есть решение уравнения (2)
и, наоборот, если ψ:
J →
Φ(U) — решение уравнения (2),
то φ(t) =
Φ–1[ψ(t)] —
решение уравнения (1) (см. рис. 5).
Действительно, если φ′(t)
≡ f[φ(t)] и
ψ(t) =
Φ[φ(t)], то
|
ψ′(t) =
dΦ[φ(t)][φ′(t)]
= dΦ[φ(t)](f[φ(t)]) =
|
|
= dΦ[Φ–1(ψ(t))](f[Φ–1(ψ(t))])
= F[ψ(t)]. |
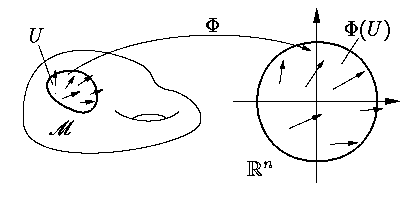
Рис. 5.
Задача О5.1. Докажите обратное утверждение.
В силу сказанного вся локальная теория обыкновенных дифференциальных уравнений без труда
переносится на дифференциальные уравнения на многообразиях.
Задача О5.2. Докажите, что для любых
t0 ∈ R
и x0 ∈
M найдется такое T > 0,
что уравнение (1)
имеет на [t0 – T,
t0 + T] единственное решение,
удовлетворяющее начальному условию x(t0) = x0.
Поэтому в теории дифференциальных уравнений на многообразиях нетривиальными и содержательными
являются лишь утверждения о глобальном поведении траекторий. Простейшим примером такого
утверждения может служить важная
Теорема о глобальной продолжимости траекторий на многообразии.
Если M — компактное многообразие,
то любое решение уравнения (1)
продолжимо на всю ось.
Д о к а з а т е л ь с т в о. Пусть φ:
J → M —
максимальное решение
уравнения (1). Нам нужно показать, что J = R.
Допустим противное: J = (a, b)
и, например, b < +∞.
Пусть {tk} ⊂ J
и tk → b
при k → ∞.
В силу компактности M, не ограничивая общности, можно считать, что
φ(tk) →
x0 ∈ M при
k → ∞. Обозначим через ψ:
(b – ε, b +
ε) → M
решение уравнения (1), удовлетворяющее начальному условию
x(b) = x0 (будем считать, что
b – ε > a).
Задача О5.3. Покажите, что φ(t)
≡ ψ(t)
при t ∈ (b – ε, b).
Если теперь определить функцию ξ:
(a, b+ε)
→ M
формулой
| ξ(t) = | { |
φ(t) при t
∈ (a, b – ε/2),
ψ(t) при t∈
{b – ε/2, b + ε), |
|
то, как легко видеть, ξ
будет продолжением
решения φ, что противоречит его
максимальности. Аналогично
показывается, что a = –∞.
Условие компактности многообразия M в вышеприведенной теореме
существенно.
Задача О5.4. Пусть M =
(0, 1) ⊂ R и топология на M
наследуется из R. Решения уравнения x′ = 1
на M не продолжимы
на всю ось.
Задача О5.5. Пусть M = R.
Покажите, что уравнение x′ = x2
на M имеет непродолжимые
на всю ось решения.
Доказанная теорема вкупе с единственностью решения (гарантируемой гладкостью правой части
уравнения) позволяют построить оператор сдвига
gt: M →
M вдоль траекторий уравнения (1) за время от
0 до t.
Задача О5.6. Проведите полное доказательство.
Задача О5.7. Покажите, что g0 —
тождественное отображение на M и
gt+s =
gt·gs
при любых t, s ∈ R.
Кроме того, можно показать, что при каждом
t ∈ R
отображение gt является Cr-диффеоморфизмом
на M. Однопараметрическая группа {gt}
диффеоморфизмов на M часто называется
потоком на многообразии
M, определяемым векторным полем
f (или уравнением (1)).
Верно и обратное утверждение: Однопараметрическая группа {gt}
Cr-диффеоморфизмов на многообразии M
такая, что g0 = I и
gt+s =
gt·gs
является оператором сдвига (потоком), отвечающим векторному полю
| f(x) = | ( |
d
dt
|
gt(x) |
) | | |
x = 0 | . |
|
Задача О5.8. Докажите это утверждение.
Классическая глобальная теория — теория
Пуанкаре — Бендиксона — для дифференциальных
уравнений на многообразиях в общем случае не имеет места. Мы приведем один пример нарушения
теоремы Пуанкаре — Бендиксона
и опишем один случай ее выполнения.
Двумерный тор T2 (поверхность "бублика"),
по определению, это прямое произведение двух окружностей: T2 =
S1×S1
(см. рис. 6). Его можно также представлять как квадрат
[0, 2π]×[0, 2π]
с отождествленными противоположными сторонами или (что нам наиболее
удобно) как плоскость с отождествленными точками, координаты
которых отличаются на векторы вида (2πk,
2πn),
k, n ∈ N:
T2 =
R2/2πN2
(см. рис. 6). Отображение
c: R2 →
T2, задаваемое формулой
|
c(x1, x2) = (x1
modd 2π, x2 modd 2π)
∈ S1×S1 |
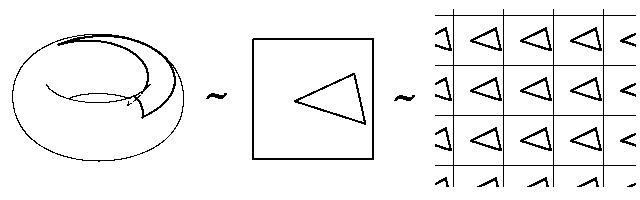
Рис. 6.
(здесь a modd 2π — "остаток" от деления a на
2π, т. е. число b
∈ [0, 2π)
такое, что a = 2πk + b
при некотором k ∈ N),
и обратное к нему (многозначное отображение устанавливает взаимно однозначное соответствие между
векторными полями на торе и 2π-периодическими
по обеим переменным векторными полями на R2 (т. е. векторными полями
f(x1, x2) такими, что
f(x1 + 2πk,
x2 + 2πn)
≡ f(x1, x2)).
Простейшим примером, показывающим невыполнимость теоремы
Пуанкаре — Бендиксона для дифференциальных уравнений
на торе, является дифференциальное уравнение, которое
порождается (в соответствии с вышеописанной процедурой) дифференциальным уравнением на
R2 вида
Если отношение α2/α1
рационально (в этом случае соответствующий поток называют рациональной
обмоткой тора), то любая траектория на торе — замкнутая
периодическая орбита, т. е. цикл
(см. рис. 7).
Задача О5.9. Докажите!
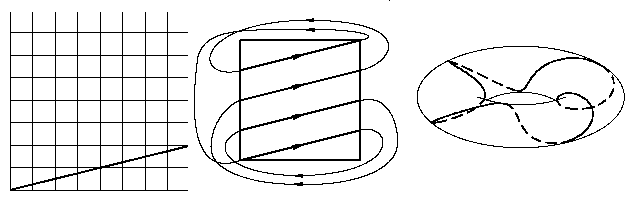
Рис. 7.
Если же это отношение иррационально (в этом случае говорят об
иррациональной обмотке тора), то любая траектория плотна на
T2, вернее,
ω-предельным
множеством любой траектории является весь
тор (см. рис. 8),
хотя у соответствующего векторного поля и нет
стационарных точек.
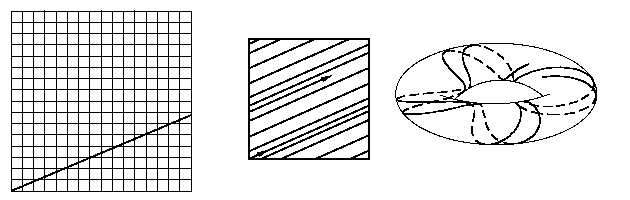
Рис. 8.
Задача О5.10. Докажите это, воспользовавшись
тем фактом, что любая аддитивная подгруппа группы R либо плотна в R, либо дискретна.
Причиной нарушения теоремы
Пуанкаре — Бендиксона на
торе является отсутствие аналога теоремы
Жордана, т. е. наличие на торе замкнутых кривых без самопересечений, которые
не делят тор на две связные компоненты.
В отличие от тора, на двумерной сфере S2 теорема Жордана выполнена.
Поэтому имеет место
Теорема Пуанкаре — Бендиксона на сфере. Пусть f:
S2 →
TS2 —
Cr+1-гладкое
векторное поле, φ:
R → S2 — решение
уравнения (1), отвечающего этому полю. Тогда, если
ω-предельное множество
Ω(Tφ)
не содержит стационарных точек,
то оно является циклом.
Литературные указания. Язык теории дифференциальных
уравнений на многообразиях — это язык современной теории обыкновенных дифференциальных уравнений
(см., напр., [Арнольд,
Арнольд,
Итоги науки и техники...]).
Потребность в их изучении появилась давно в связи с задачами
описания механических систем с голономными связями
[Арнольд]. Литература по теории
дифференциальных уравнений на многообразиях весьма обширна. Мы
приводим, помимо уже цитированных, лишь классические книги
полностью или частично, посвященные этому вопросу:
[Андронов —
Леонтович — Гордон — Майер,
Коддингтон — Левинсон,
Немыцкий — Степанов,
Нитецки,
Палис — ди Мелу,
Хартман].
Задачи. О5.11. Пусть
gt — поток на M и
M1, M2 —
инвариантные множества потока, т. е.
gt(Mi)
⊆ Mi
(i = 1, 2) при всех t ∈
R. Докажите, что множества
M1 ∪ M2,
M1 ∩ M2
и M1\M2
также инвариантны.
О5.12. Пусть Tφ —
траектория решения уравнения (1).
Докажите, что ω-предельное
множество Ω(Tφ)
инвариантно относительно потока, определяемого
уравнением (1).
О5.13. Пусть M компактно. Докажите, что
Ω(Tφ)
непусто, компактно и связно.
О5.14. Пусть M = S2
и выполнены условия теоремы
Пуанкаре — Бендиксона на сфере.
Пусть y ∈
Ω(Tφ), а
S — лежащее в достаточно малой окрестности
Vy точки y Cr-гладкое
одномерное подмногообразие, содержащее точку y и трансверсальное
f(y) (последнее означает, что векторы f(y) и
TyS в
TyS2
пересекаются под ненулевым углом). Пусть, наконец, xi =
φ(ti) —
последовательные точки пересечения траектории
Tφ с
подмногообразием (дугой) S. Покажите, что последовательность
{xi} "монотонна" в том смысле, что xi на S
лежит между точками xi–1
и xi+1 при всех достаточно
больших i.
О5.15. В условиях предыдущей задачи
Ω(Tφ)
∩ S = {y} (если, разумеется, окрестность
Vy достаточно мала).
О5.16. Пользуясь результатами двух предыдущих задач, докажите
теорему Пуанкаре — Бендиксона на сфере.
О5.17. Докажите, что если векторное поле на S2 имеет
(отличный от стационарной точки)
цикл, то оно имеет по крайней мере две стационарные
точки (ср. с теоремой о стационарной точке).
О5.18. Приведите пример дифференциального уравнения на сфере
S2, имеющего траекторию,
ω-предельное
множество которой представляет собой замкнутую кривую, состоящую из
стационарных точек.
О5.19. Приведите пример дифференциального уравнения на трехмерном торе
T3 = S1 ×
S1×S1,
ω-предельное
множество каждой траектории которого совпадает
с T3.
О5.20. Пусть дифференциальное уравнение на торе
T2 таково, что соответствующее уравнение на плоскости имеет вид
|
x′1= 1,
x′2=
f(x1, x2).
| (4) |
Числом вращения
μ(φ)
траектории Tφ на торе называется предел
limt→∞ψ2(t)/ψ1(t),
где (ψ1,
ψ2) — соответствующее решению
φ решение уравнения (4).
Пусть уравнение на торе имеет периодическую траекторию. Докажите,
что для любой траектории предел, определяющий
μ(φ), существует.
О5.21. Покажите, что в условиях предыдущей задачи число
μ(φ)
не зависит от φ. Поэтому число μ =
μ(φ)
называют числом вращения уравнения или векторного поля.
О5.22. Докажите, что в задачах 20, 21 можно опустить требование
существования периодической траектории.