§ 1.5. О составлении дифференциальных уравнений

Дифференциальные уравнения представляют математический язык, на котором естественно записываются многие законы природы. В этом параграфе мы рассмотрим несколько примеров составления дифференциальных уравнений для прикладных задач.

1.5.1. Уравнения Лагранжа для механических систем. Рассмотрим систему из N свободных материальных точек Aj с массами mj (j = 1, ..., m). Пусть в некоторой декартовой инерциальной системе координат (т. е. в такой, в которой справедлив второй закон Ньютона) радиус-вектор точки Aj есть rj = rj(t); тогда ее скорость и ускорение вычисляются через производные от rj: vj = r.j,aj = r..j (в классической механике производная по времени традиционно обозначается точкой). Допустим, что сумма всех внешних и внутренних сил, приложенных к Aj, есть функция Fj(t, r, r.j), где r = (r1, r2, ..., rN). Тогда данная механическая система описывается по второму закону Ньютона системой ОДУ

mr..j = Fj(t, r, r.j)    (j = 1, 2, ..., N).

(1)

Таким образом, второй закон Ньютона дает общий метод описания механических систем с помощью дифференциальных уравнений.

Пусть на систему наложены связи (например, точки соединены жесткими стержнями пренебрежимо малой массы и т. п.) Тогда 3N-мерная точка r, изображающая мгновенное положение всей системы, уже не может принимать произвольное положение в R^3N, а вынуждена в каждый момент времени t принадлежать некоторому множеству K_t ⊂ R^3N, называемому конфигурационным многообразием данной механической системы.

Мы будем предполагать, что конфигурационное многообразие допускает следующее описание. Пусть t0 ∈ R, r0 ∈ Kt0. Тогда должны существовать окрестность U ⊂ R точки t0 и окрестность V ⊂ R3N точки r0 такие, что для любого t ∈ U любая точка r ∈ Kt ∩ V однозначно записывается в виде

r = r(t, q),

(2)

где функция r(t, q) определена по q = (q₁, ..., q_n) на открытом множестве Q ⊂ Rⁿ (n ≤ 3N), дважды непрерывно дифференцируема по совокупности переменных и невырождена в том смысле, что (3N×n)-матрица Якоби ∂r/∂q имеет максимальный возможный ранг n. Координаты q₁, ..., q_n вектора q, которые по любым t ∈ U и r ∈ K_t ∩ V находятся однозначно, называются локальными обобщенными, или лагранжевыми координатами точки r.

Выбор локальных обобщенных (или просто обобщенных) координат, конечно, неоднозначен. Число n называется размерностью конфигурационного многообразия.

Для системы со связями в правых частях уравнения (1) появляются неизвестные заранее силы реакции связей. Если связи идеальны, (т. е. соответствующие силы реакции не производят работы), то задача, тем не менее, остается динамически определенной, так как уравнения связей (2) дают необходимую дополнительную информацию.

Однако практически бывает удобно рассматривать вместо(1), (2) эквивалентную ей систему уравнений Лагранжа второго рода, записанную непосредственно в обобщенных координатах q_i и не содержащую сил реакции связей. Вывод уравнений Лагранжа дается в курсе теоретической механики, здесь мы только опишем алгоритм построения этих уравнений, состоящий из трех шагов.

1) Выражение кинетической энергии системы через обобщенные координаты:

T = N ∑ j = 1 mjv2j 2   =   1 2 N ∑ j = 1 mjr.j2  =   1 2 N ∑ j = 1 mj ( ∂rj ∂t   +   ∂rj ∂q q. ) 2 .

Здесь rj в соответствии с (2) считается функцией t и q; r.j= drj/dt вычисляется как производная сложной функции; квадрат вектора — его скалярный квадрат.

2) Вычисление обобщенных сил :

Qi = N ∑ j = 1 Fj ∂rj ∂qi    (i = 1, 2, ..., n).

3) Выписывание уравнений Лагранжа:

d dt ∂T ∂q.i   –   ∂T ∂qi   = Qi   (i = 1, 2, ..., n).

1.5.2. Уравнения гармонического осциллятора и маятника. Составим уравнения Лагранжа для двух конкретных механических систем, изображенных на рис. 1.

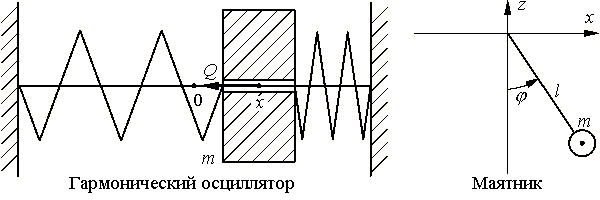
Рис. 1.

Гармонический осциллятор — это грузик на гладком стержне, поддерживаемый с двух концов пружинами. Для него в качестве единственной обобщенной координаты можно взять декартову координату x; для маятника естественно выбрать φ (см. рис. 1). Тогда уравнения (2) для этих систем запишутся в виде

r =  ( x 0 0 ) ;

r =  ( t·sin φ 0 – t·cos φ ) ;

Для маятника эта функция взаимно однозначна при φ ∈ (–π, π) и при φ ∈ (0, 2π) (две локальные системы координат).

Далее, кинетическая энергия этих механических систем вычисляется по формулам

T = mx.2 2

T = m 2 [(tφ.cos λ)2 + (tφ.sin λ)2] = 1 2 mt2φ.2,

а обобщенные силы — по формулам

Q = – kx · ( 1 0 0 ) · ∂r ∂x = –kx · ∂r ∂x

Q = –mg · ( 0 0 1 ) · ∂r ∂φ = –mg · ∂r ∂φ = –mgt ·sin φ

(в гармоническом осцилляторе это сила пружин по закону Гука, а в маятнике — сила земного тяготения). Промежуточные вычисления тривиальны:

∂T ∂q1  =  ∂T ∂x.  = mx.;

∂T ∂q.1  =  ∂T ∂φ  = ml2φ.;

d dt ∂T ∂q1  = mx..;

d dt ∂T ∂q1  = ml2φ..;

∂T ∂q1  =  ∂T ∂x  = 0;

∂T ∂q1  =  ∂T ∂φ  = 0.

Таким образом, уравнения движения имеют вид:

mx.. = –kx;

ml2φ.. = –mgl·sin φ,

или в окончательном виде, для гармонического осциллятора:

x.. + ω2x = 0    (ω2 = k/m),

(3)

а для маятника:

φ.. + ω2sin φ = 0    (ω2 = g/l).

(4)

Если длина стержня маятника изменяется во времени: l = l(t), то выражение для для кинетической энергии T будет более сложным, однако нетрудно проверить, что окончательное уравнение будет иметь вид (4) с ω = ω(t) = [g/l(t)]^1/2 (проверьте).

Описанный здесь способ построения уравнений движения механических систем является универсальным и наиболее удобным. Лишь в тех случаях, когда связи совсем просты (как, например, для гармонического осциллятора), удобнее пользоваться вторым законом Ньютона (проделайте это для гармонического осциллятора).

1.5.3. Уравнение RLCE-контура. Рассмотрим электрическую цепь, изображенную на рис. 2. Она состоит из четырех двухполюсников : сопротивления R, индуктивности L, емкости C и источника ЭДС E. Если для двухполюсника A произвольно выбрать положительное направление, то в любой момент времени ему можно сопоставить две величины: напряжение u_A (вольт) и ток i_A (ампер). При смене положительного направления они меняют знак. Каждый из двухполюсников описывается определенным уравнением:

uR = RiR,  L diL dt  = uL,  C duC dt  = iC,  uE = – e(t).

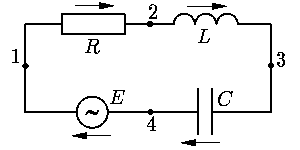
Рис. 2.

Неотрицательные параметры R (ом), L (генри) и C (фарада) называются, как и сами двухполюсники, сопротивлением, индуктивностью и емкостью; заданная функция e(t) характеризует источник ЭДС. Соединения двухполюсников в цепь описываются двумя законами Кирхгофа. Первый закон Кирхгофа гласит: сумма токов, втекающих в любой узел, равна нулю. В рассматриваемом контуре четыре узла, они помечены цифрами. Из закона Кирхгофа для узла 1 следует, что i_E = i_R, так как в этот узел втекают токи i_E и –i_R. Из рассмотрения остальных узлов следует, что ток во всем контуре один:

iE = iR = iL = iC = i.

Второй закон Кирхгофа утверждает, что сумма напряжений при обходе любого замкнутого контура равна нулю (положительные направления двухполюсников должны быть согласованы с направлением обхода).

В нашем случае:

uR + uL + uC + uE = 0,

или

L di dt + uC + Ri = e(t).

Из уравнения емкости следует, что

i = C duC dt ,  di dt  = C d2uC dt2 .

Введя обозначение u = u_C, получаем окончательно:

LCu′′ + RCu′ + u = e(t).

(5)

Это — уравнение RLCE-контура. В него входит только напряжение емкости u; все остальные напряжения и токи вычисляются по u:

i = Cu′,  uR = Ri,  uC = e(t) – u – uR.

Заметим, что при R = 0 и e(t) = 0 полученное уравнение лишь обозначениями отличается от уравнения гармонического осциллятора. Здесь проявляется универсальность языка дифференциальных уравнений: он выявляет существенные связи между разными уравнениями. Для уравнения (5) роль величины ω из (3) играет 1/(LC)^1/2.

1.5.4. Модель биологической системы "хищник-жертва". В качестве последнего примера приведем вывод уравнений, описывающих изменение численности двух взаимосвязанных биологических видов: "жертвы" (N₁) и "хищника" (N₂) по книге известного итальянского математика Вито Вольтерры. Встречающийся в этом выводе термин "коэффициент прироста" обозначает отношение N′/N скорости изменения численности вида к его численности. В подобных моделях функцию удобно считать гладкой, хотя на самом деле она принимает целочисленные значения и, следовательно, изменяется скачкообразно. Поскольку модель носит приближенный характер, такая интерпретация допустима. Итак, цитируем текст на с. 21 – 22.

"Если бы в среде, где обитают эти виды, находился только один из них, а именно жертва, то у него был бы некоторый коэффициент прироста ε₁, который мы будем предполагать постоянным и положительным. Другой вид (хищник), питающийся только (или в основном) жертвой, в предположении, что он существует изолированно, имеет некоторый коэффициент прироста –ε₂, который мы будем считать постоянным и отрицательным. Когда два такие вида сосуществуют в ограниченной среде, первый будет развиваться тем медленнее, чем больше существует индивидуумов второго вида, а второй — тем быстрее, чем многочисленнее будет первый вид. Гипотеза, довольно простая, состоит в том, что коэффициенты прироста равны соответственно

ε1 – γ1N2 и  –ε2 + γ2N1

(γ₁, γ₂ — положительные постоянные). Это приводит к системе дифференциальных уравнений для описания численности видов:

dN1 dt = N1(ε1 – γ1N2),

dN2 dt = –N2(ε2 – γ2N1)  (ε1,ε2, γ1, γ2 > 0)."

Эта цитата показывает, что при выводе дифференциальных уравнений помимо строгих законов нередко используются гипотезы и различные приближенные представления.

1.5.5. Задачи

1.5.5.1. Найдите все функции вещественного аргумента, графики которых обладают следующим свойством: абсцисса точки пересечения любой касательной с осью абсцисс вдвое меньше абсциссы точки касания.

1.5.5.2. Закон радиоактивного распада утверждает, что количество распавшегося за единицу времени вещества пропорционально количеству этого вещества в данный момент времени. Периодом полураспада радиоактивного вещества называется время, за которое количество вещества уменьшается вдвое. Из каждого грамма радия за год распадается 0.44 мг. Чему равен период полураспада радия?

1.5.5.3. Период полураспада радиоактивного углерода C614 равен 5568 лет. За какое время от одного мг C614 останется 0.001 мг? (На измерении количества радиоактивного углерода основан один из методов датировки палеонтологических находок.)

1.5.5.4. Пружина длиной 1 м удлиняется под действием силы 1 н в два раза. Во сколько раз удлинится такая же пружина длиной 3 м под действием собственного веса, если 1 м пружины весит 5 н?

1.5.5.5. Найдите время падения футбольного мяча с высоты 30 м, если известно, что сопротивление воздуха пропорционально квадрату скорости и при скорости 1 м/сек оно равно 0.5·10^–4 н.

File based on translation from T_EX by T_TH, version 2.32.
Created 3 Jan 2002, 01:21.
Last modified 10 Apr 2002.