§ О12. Динамические системы на плоскости

Тот факт, что траектории автономной системы дифференциальных уравнений

x′ = f(x)

(1)

(f: R² → R² — удовлетворяющая условию Липшица функция) представляют собой плоские кривые позволяет извлечь значительно бóльшую информацию о поведении траекторий, нежели в общем случае, описанном в очерке О11. Основную роль здесь играет то обстоятельство, что непрерывная замкнутая кривая без самопересечений делит плоскость на две связные части (теорема Жордана). Это обстоятельство резко ограничивает свободу движений фазовых точек системы (1). В частности, если какая-либо траектория начинается внутри области, ограничиваемой некоторым циклом, то она все время остается внутри этой области, поскольку две траектории не могут пересекаться (почему?).

Излагаемая ниже теория (вернее, ее основы) носит название теории Пуанкаре — Бендиксона. Она описывает структуру траекторий двумерной динамической системы, в особенности, их свойства в окрестностях циклов и стационарных точек.

Основное утверждение теории Пуанкаре — Бендиксона грубо можно сформулировать так: ограниченные предельные множества, не содержащие стационарных точек, являются циклами, на которые "наматываются" (или с которых "сматываются") близлежащие траектории. Следует подчеркнуть, что фактически каждая из доказываемых теорем в пространствах размерности большей двух не имеют места.

Теорема о траектории, содержащей предельную точку. Пусть T_φ — траектория системы (1) и T_φ ∩ [Ω(T_φ) ∪ A(T_φ)] ≠ ∅. Тогда T_φ является либо циклом, либо стационарной точкой.

Д о к а з а т е л ь с т в о.   Пусть точка x₀ лежит, например в T_φ ∩ Ω(T_φ). Если точка x₀ стационарная, то очевидно, T_φ = {x₀} и теорема доказана.

Пусть теперь x₀ не является стационарной точкой системы (1). Тогда в любой достаточно малой окрестности V точки x₀ поле направлений, порождаемое функцией f, почти параллельно вектору f(x₀). Обозначим через x₁ первое пересечение траектории g^tx₀ (t ≥ 0) с прямой L, ортогональной вектору f(x₀) и проходящей через точку x₀ + εf(x₀), где ε — достаточно малое положительное число (см. рис. 1). Поскольку точка x₀ является ω-предельной, полутраектория g^t(x₀) (t ≥ 0), миновав точку x₁, должна рано или поздно вернуться в окрестность V. Если окрестность V и число ε достаточно малы, то траектория должна вторично пересечь прямую L, скажем в точке x₂ (см. рис. 1). Когда точки x₁ и x₂ совпадают, траектория T_φ, очевидно замкнута и теорема доказана.

Рис. 1.

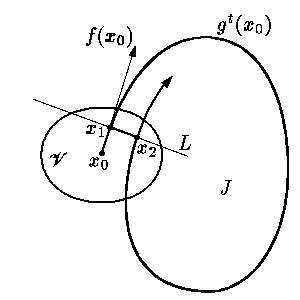
В случае x₁ ≠ x₂ рассмотрим замкнутую непрерывную кривую без самопересечений (жорданову кривую), образованную частью траектории T_φ, находящейся между точками x₁ и x₂, и отрезком [x₁, x₂] прямой L. По теореме Жордана эта кривая делит плоскость на две части. Пусть J — внутренняя из них (она называется мешком Бендиксона). Теперь легко видеть, что либо траектория T_φ, попав в мешок J (после точки x₂), никогда его не покинет (см. рис. 1), либо, выйдя из мешка J (после точки x₂), никогда уже в него не попадет (см. рис. 2). И в том и в другом случае траектория навсегда покидает достаточно малую окрестность точки x₀, что противоречит ее ω-предельности.

Рис. 2.

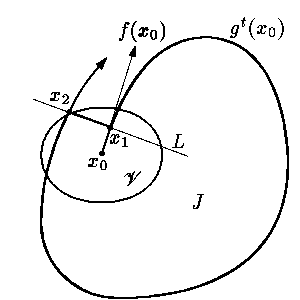
Задача О12.1. Восстановите детали доказательства.

Как уже отмечалось в очерке О11 при исследовании окрестностей циклов важную роль играет функция последования G. В двумерном случае эта функция определена в окрестности точки x₀ прямой L, трансверсальной циклу T_φ в точке x₀ ∈ T_φ, и принимает значения в L (см. рис. 3). Введем на L линейные координаты с нулем в точке x₀. Тогда функцию G можно рассматривать как скалярную функцию, определенную в окрестности нуля вещественной прямой. В силу результатов задачи О11.8 она непрерывна и, кроме того, G(0) = 0.

Задача О12.2. Докажите, что в малой окрестности цикла T_φ нет отличных от T_φ циклов в том и только том случае, когда уравнение G(x) = x не имеет малых ненулевых решений.

Рис. 3.

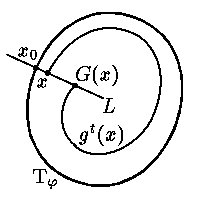
Оказывается, функция G строго монотонна. Доказательство этого утверждения изображено на рис. 4.

Рис. 4.

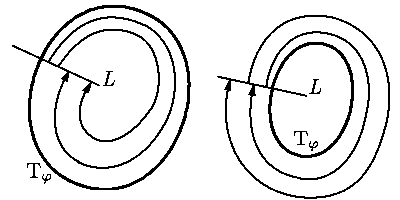
Задача О12.3. Проведите полное доказательство.

Допустим, что в окрестности цикла T_φ отсутствуют другие циклы. Тогда в силу задачи 2 уравнение G(x) = x не имеет в окрестности ненулевых решений. Таким образом, графики функций y = G(x) и y = x в малой окрестности нуля пересекаются только в нулевой точке. Их взаимное расположение полностью определяет асимптотическое поведение траекторий в окрестности цикла T_φ при t → ±∞. Мы будем различать четыре качественно различных случая, изображенных на рис. 5.

Рис. 6.

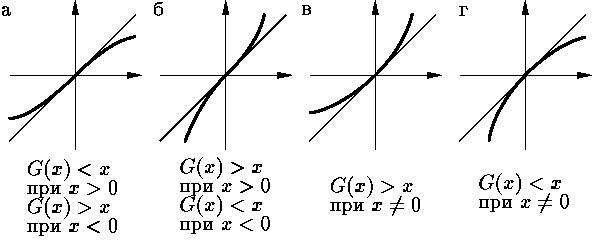
Будем говорить, что цикл T_φ отрицательно орбитально асимптотически устойчив, если он орбитально асимптотически устойчив при t → –∞. Другими словами, близлежащие траектории "спиралеобразно наматываются" на цикл T_φ при t → –∞.

Задача О12.4. Докажите, что отрицательно орбитально устойчивый цикл не является орбитально устойчивым.

Цикл T_φ называется асимптотически полуустойчивым, если близкие к нему траектории, лежащие внутри T_φ (или вне T_φ), ведут себя так же, как ведут себя траектории около орбитально асимптотически устойчивого цикла, а близкие в нему траектории, лежащие вне T_φ (соответственно, внутри T_φ) — как траектории около отрицательно орбитально асимптотически устойчивого цикла.

Задача О12.5. Сформулируйте формальное определение асимптотически полуустойчивого цикла.

Теорема о свойствах устойчивости цикла. Любой изолированный цикл двумерной автономной системы является либо орбитально асимптотически устойчивым, либо отрицательно орбитально асимптотически устойчивым, либо асимптотически полуустойчивым.

Д о к а з а т е л ь с т в о.  Орбитально асимптотически устойчивый случай отвечает поведению функции G, изображенному на рис. 5а, отрицательно орбитально асимптотически устойчивый — рис. 5б, асимптотически полуустойчивый — 5в и 5г. Соответствующее поведение траекторий изображено на рис. 6 а – г (если считать, что координаты на прямой L введены так, что точки с малыми отрицательными координатами лежат внутри цикла T_φ). Доказательство сводится к использованию формулируемой ниже задачи и теоремы о непрерывной зависимости от начальных данных.

Задача О12.6. Докажите, что: а) G^k(x) → 0 при k → ∞ для малых x, если либо x > 0 и G(y) < y при малых положительных y, либо x < 0 и G(y) > y при малых отрицательных y; б) G^–k(x) → 0 при k → ∞ для малых x, если либо x > 0 и G(y) > y при малых положительных y, либо x < 0 и G(y) < y при малых отрицательных y.

Рис. 6.

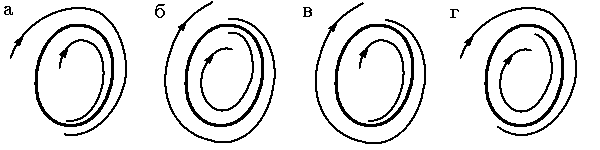
Если цикл не является изолированным, то во всех предыдущих определениях и рассуждениях надо опустить слово "асимптотически". Таким образом, любой цикл является либо орбитально устойчивым, либо отрицательно орбитально устойчивым, либо полуустойчивым.

Задача О12.7. Докажите последнее утверждение.

Основным утверждением теории Пуанкаре — Бендиксона является следующая

Теорема о предельном цикле. Пусть T_φ — ограниченная положительная (соответственно, отрицательная) полутраектория двумерной автономной системы. Тогда, если Ω(T_φ) (соответственно, A(T_φ)) не содержит стационарных точек, то Ω(T_φ) (соответственно, A(T_φ)) является циклом.

Д о к а з а т е л ь с т в о.  По теореме о структуре ω-предельных множеств Ω(T_φ) ≠ ∅. Пусть x₀ ∈ Ω(T_φ) и T_ψ = {g^t(x₀): t ∈ R} — траектория, проходящая через точку x₀. По теореме об инвариантности предельных множеств T_ψ ⊆ Ω(T_φ) и следовательно Ω(T_ψ) ⊆ Ω(T_φ).

Докажем, что T_ψ есть цикл. Пусть x₁ ∈Ω(T_ψ). Тогда по условию f(x₁) ≠ 0 и в малой окрестности V точки x₁ векторное поле f(x) почти параллельно вектору f(x₁). Обозначим через L прямую, проходящую через точку x₁ и ортогональную вектору f(x₁) (см. рис. 7). Так как x₁ ∈ Ω(T_ψ), в малой окрестности V, а поэтому и на интервале V ∩ L есть точки траектории T_ψ. Обозначим через y₁, y₂ и y₃ три последовательные точки пересечения траектории T_ψ с интервалом V ∩ L. Если хотя бы две из них совпадают, то T_ψ — цикл.

Рис. 7.

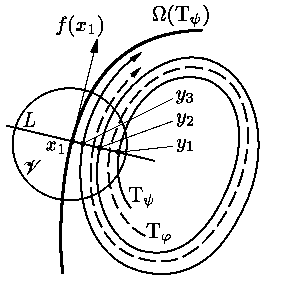
Если предположить, что y_i ≠ y_j при i ≠ j, то точка y₂ расположена на этом интервале между точками y₁ и y₃. Поскольку траектории не могут пересекаться, а векторное поле f(x) в V почти параллельно вектору f(x₁), траектория T_φ (она изображена пунктиром на рис. 7) не может пересекать отрезки [y₁, y₂] и [y₂, y₃] более одного раза, что противоречит условию y₂ ∈ Ω(T_φ). Таким образом, T_ψ — цикл.

Задача О12.8. В завершение доказательства покажите, что T_ψ = Ω(T_φ). Восстановите детали доказательства.

В заключение очерка приведем признаки существования циклов и стационарных точек. Простейший из них вытекает из теоремы о предельном цикле: для того, чтобы система (1) имела цикл или стационарную точку необходимо и достаточно существования хотя бы одной ограниченной полутраектории. Действительно, если T_φ — ограниченная, например, вправо полутраектория, то либо в Ω(T_φ) содержатся стационарные точки, либо Ω(T_φ) — цикл в силу упомянутой теоремы. Необходимость очевидна.

Доказательство следующей теоремы мы переносим в очерк Топологические методы в теории дифференциальных уравнений. Там оно будет получено как следствие общего утверждения.

Теорема о стационарной точке.Внутри любого цикла двумерной автономной системы есть хотя бы одна стационарная точка.

В силу этой теоремы множество без стационарных точек, содержащее цикл необходимо "кольцеобразное".

Критерий Пуанкаре — Бендиксона. Пусть Γ₁ и Γ₁ — две жордановы кривые, причем Γ₁ лежит внутри Γ₁. Пусть D — кольцевая область, лежащая между Γ₁ и Γ₁, а D — ее замыкание. Тогда, если D не содержит стационарных точек и является положительно или отрицательно инвариантным множеством, то в D — есть по крайней мере один цикл.

Задача О12.9. Докажите критерий Пуанкаре — Бендиксона.

Литературные указания. Так же, как и в предыдущем очерке, мы ограничимся перечислением классических учебников [Андронов — Витт — Хайкин, Коддингтон — Левинсон, Немыцкий — Степанов, Петровский, Рейссиг — Сансоне — Конти, Хартман].

Задачи. О12.10. Приведите пример не являющейся циклом траектории T_φ трехмерной автономной системы уравнений такой, что T_φ ∩ Ω(T_φ) ≠ ∅.

О12.11. Пусть траектория T_φ системы (1) такова, что Ω(T_φ) гомеоморфно отрезку. Докажите, что каждая точка множества Ω(T_φ) стационарна.

О12.12. Пусть T_φ — цикл системы (1), а правая часть f системы непрерывно дифференцируема. Докажите, что

G′(0) = exp ( ∫ T 0 Tr fx′[φ(t)]dt ) ,

где T — минимальный положительный период решения φ, f_x′[φ(t)] = df/dx|_x=φ(t), а Tr A — след матрицы A.

О12.13. Пусть T_φ — асимптотически полуустойчивый цикл системы (1) с непрерывно дифференцируемой правой частью. Докажите, что G′(0) = 1.

О12.14. Докажите, что асимптотически орбитально устойчивые, отрицательно асимптотически орбитально устойчивые и асимптотически полуустойчивые циклы изолированы.

О12.15. Теорему о свойствах устойчивости циклов можно переформулировать так: если T_φ — изолированный цикл системы (1) и x₀ лежит в малой окрестности T_φ, то g^t(x₀) неограниченно приближается к циклу T_φ либо при t → +∞, либо при t → –∞. Приведите пример, показывающий, что это утверждение в трехмерном пространстве не имеет места.

О12.16. Пусть T_φ — цикл системы (1), а T_ψ — некоторая внутренняя по отношению к циклу T_φ траектория такая, что Ω(T_ψ) = T_φ. Докажите, что для любой траектории T_ξ, лежащей внутри цикла T_φ, T_φ ≠ A(T_ξ).

О12.17. Докажите, что если цикл T_φ является ω-предельным множеством траектории T_ψ и T_ψ лежит внутри цикла T_φ, то T_φ является ω-предельным множеством всех достаточно близких к T_φ и внутренних по отношению к нему полутраекторий.

О12.18. Пусть T_φ⁺ — незамкнутая ограниченная полутраектория. Докажите, что если точка x₀ достаточно близка к φ(0), то положительная полутраектория {g^tx₀} незамкнута.

О12.19. Пусть D — замыкание ограниченной положительно инвариантной относительно системы (1) области, не содержащее стационарных точек этой системы. Докажите, что для любой полутраектории Tφ+⊂ D либо Tφ+— цикл, либо Ω(Tφ+)— цикл.

О12.20. Пусть T_φ и T_ψ — циклы системы (1), причем T_ψ лежит внутри T_φ. Циклы T_φ и T_ψ называются соседними, если в области D, заключенной между ними, нет циклов и стационарных точек системы (1). Докажите, что для любой траектории T_ξ ⊂ D либо Ω(T_ξ) = T_φ и A(T_ξ) = T_ψ, либо Ω(T_ξ) = T_ψ и A(T_ξ) = T_φ.

О12.21. Пусть T_φ, T_ψ и T_ξ — циклы системы (1), причем пары T_φ, T_ψ и T_ψ, T_ξ являются соседними. Докажите, что если T_φ и T_ξ асимптотически орбитально устойчивы, то цикл T_ψ отрицательно асимптотически орбитально устойчив, а если T_φ и T_ξ отрицательно асимптотически орбитально устойчивы, то цикл T_ψ асимптотически орбитально устойчив.

О12.22. Пусть Tφ+— ограниченная полутраектория, а Ω(Tφ+) содержит в точности одну стационарную точку x0. Докажите, что либо Ω(Tφ+)= {x0}, либо Ω(Tφ+)\{x0} есть (незамкнутая) траектория.

О12.23. Пусть правая часть системы (1) непрерывно дифференцируема. Пусть в некоторой односвязной области D след матрицы f ′(x) не меняет знака. Докажите, что в области D нет циклов системы (1).

File based on translation from T_EX by T_TH, version 2.32.
Created 21 Jan 2000, 00:31.
Last modified 25 Apr 2002.