§ О1. Теорема Пеано и интегральная воронка

Как мы знаем, непрерывность правой части уравнения

x′ = f(t, x)

(1)

(f : R×Rⁿ → R) и условие Липшица по x гарантируют однозначную разрешимость на всей оси задачи Коши для уравнения (1) с любыми начальными условиями. С другой стороны, отказ от условия Липшица для функции f по x, как показывает пример задачи Коши (см. п. 2.1.4).

x′ = x2,   x(0) = 1,

может привести к отсутствию глобального (определенного на всей оси) решения и, как показывает пример задачи Коши (см. п. 2.1.5).

x′ = 2   ___ √| x | ,   x(0) = 0, —

к отсутствию единственности решения. Тем не менее, задача Коши для уравнения (1), отвечающая начальному условию

x(t0) = x0,

(2)

всегда разрешима (в общем случае неединственным образом) в некоторой окрестности точки t₀, если функция f только непрерывна. Точнее, имеет место следующая

Теорема Пеано. Пусть функция f определена на цилиндре D(f) = [t₀ – a, t₀ + a] × B(x₀, b) и непрерывна (здесь B(x₀, b) — шар в Rⁿ с центром в x₀ радиуса b). Тогда задача (1) – (2) имеет по крайней мере одно решение на отрезке [t₀ – T, t₀ + T], где T = min{a, b/M}, а M = max_{(t, x)∈D(f)}||f(t, x)||.

Здесь мы опишем три из многих возможных схем доказательства этой фундаментальной теоремы.

Первая схема основана на следующей простой идее. Пусть f_k: D(f) → Rⁿ (k ∈ N₊; обозначение N₊ закреплено за множеством натуральных чисел) — непрерывно дифференцируемые функции, удовлетворяющие неравенствам

||fk(t, x) || ≤M,    ||f(t, x) – fk(t, x) || ≤ 1 k при всех (t, x) ∈ D(f).

В качестве f_k можно взять, например, полиномиальные аппроксимации функции f, существование которых гарантирует теорема Вейерштрасса. Каждая функция f_k в силу непрерывной дифференцируемости удовлетворяет (локальному!) условию Липшица по x. Поэтому при каждом k задача Коши

x′ = fk(t, x),

x(t0) = x0

имеет на отрезке [t₀ – T, t₀ + T] в силу обобщенной теоремы Коши — Пикара единственное решение, скажем, x_k, т. е.

xk(t) = x0 + ∫ t t0 fk[s, xk(s)] ds,   t ∈ [t0 – T, t0 + T].

(3)

Построенная последовательность {xk} не обязательно сходится, но оказывается у нее есть равномерно сходящаяся подпоследовательность {xkm}. Заменяя в (3) k на km и переходя в получившемся равенстве к пределу при m → ∞, получим, что предел x* этой подпоследовательности является решением интегрального уравнения

x(t) = x0 + ∫ t t0 f[s, x(s)] ds,   t ∈ [t0 – T, t0 + T]

(4)

и, следовательно, решением задачи Коши (1) – (2).

Второй возможный путь связан с так называемыми приближениями Тонелли. Мы покажем как этим способом строится решение задачи (1) – (2) на отрезке [t₀, t₀ + T]. На отрезке [t₀ – T, t₀] решение строится аналогично. Итак, возьмем произвольную определенную на [t₀ – T, t₀] непрерывно дифференцируемую функцию φ со значениями в Rⁿ, удовлетворяющую условиям

φ(t0) = x0,    ||φ(t) – x0 || ≤ b,    ||φ′(t) || ≤ M    (t ∈ [t0 – T, t0]).

Определим теперь для любого натурального k (удовлетворяющего неравенству 1/k ≤ T) функцию y_k на отрезке [t₀ – T, t₀], положив y_k(t) = φ(t) при t ∈ [t₀ – T, t₀] и

yk(t) = x0 + ∫ t t0 f [ s, yk ( s – 1 k ) ] ds при t ∈[t0, t0 + T].

(5)

Формула (5) определяет функции yk на отрезке [t0, t0 + T] "поэтапно", шагами длины 1/k: для определения функции yk на отрезке длины 1/k нужна информация о ее поведении левее этого отрезка (подробнее см. метод шагов). Из последовательности yk можно выделить равномерно сходящуюся подпоследовательность ykm. Окончание доказательства стандартно: нужно заменить в (5) k на km и перейти к пределу при m → ∞. Тогда получим, что предел y* последовательности ykm является решением интегрального уравнения (4) на отрезке [t0, t0 + T].

Наконец, третий путь основывается на использовании ломаных Эйлера. Пусть z_k — ломаная Эйлера на [t₀, t₀ + T] с шагом сетки, равным 1/k. Нетрудно показать, что из последовательности {z_k} можно выделить равномерно сходящуюся подпоследовательность и что ее предел является решением задачи (1) – (2).

Возможность выделять сходящиеся подпоследовательности из построенных выше последовательностей {x_k}, {y_k}, {z_k} вытекает из их относительной компактности. Последний факт может быть легко доказан с помощью теоремы Арцела — Асколи (см. любой курс функционального анализа), поскольку построенные последовательности равномерно ограничены вместе со своими производными.

Задача О1.1. Реализуйте описанные выше пути доказательства теоремы Пеано.

Первые два пути позволяют исчерпать все решения задачи (1) – (2) на промежутке [t₀ – T, t₀ + T]. Третий путь, когда решение неединственно, вообще говоря, всех решений не дает.

Задача О1.2. Подтвердите последнее утверждение на примере задачи

x′ = 2√|x|    x(0) = 0,

Отметим, что если f определена на всем пространстве R×Rⁿ и ограничена, т. е. M < ∞, то задача (1) – (2) имеет по крайней мере одно решение, определенное на всей оси.

В связи с возможной неединственностью решений задачи (1) – (2) возникают различные вопросы, связанные с изучением структуры множества ее решений. Множество решений задачи (1) – (2), определенных на [t₀, τ], мы будем называть интегральной воронкой и обозначать через W_τ, а множество Ω_τ = {(t, x) ⊂ R×Rⁿ: x = y(t), y ∈ W_τ, t ∈ [t₀, τ]} будем называть воронкой. Подчеркнем, что W_τ ⊂ C[t₀, τ], а Ω_τ ⊂ R×Rⁿ (см. рис. 1). Наконец, сечение множества Ω_τ гиперплоскостью {(t, x) ⊂ R×Rⁿ: t = τ} будем обозначать через S_τ (см. рис. 1).

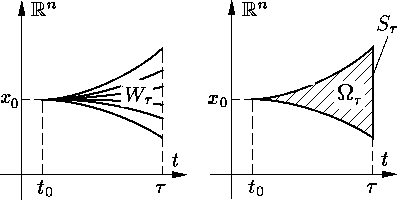
Рис. 1.

Первый результат, который мы сформулируем — это

Теорема Кнезера. В условиях теоремы Пеано при τ ∈ [t₀ – T, t₀ + T] (здесь и ниже T — число, фигурирующее в теореме Пеано) сечение S_τ является замкнутым ограниченным связным множеством.

Более того, имеет место более точный результат —

Теорема Фукухары. В условиях теоремы Пеано при τ ∈ [t₀ – T, t₀ + T] интегральная воронка W_τ (и, следовательно, воронка Ω_τ) является компактным связным множеством.

Напомним, что топологическое пространство Ω называется связным, если его нельзя разбить на два открытых непересекающихся множества (эквивалентное определение — любые две точки из Ω можно соединить непрерывной лежащей в Ω кривой).

В скалярном случае доказательство теоремы Кнезера, как, впрочем, и теоремы Фукухары, особых затруднений не вызывает, поскольку замкнутым связным множеством на прямой может быть только отрезок. Поэтому если точки x₁, x₂ ∈ S_τ, то и любая точка x₃ отрезка [x₁, x₂] лежит в S_τ — достаточно рассмотреть решение уравнения (1), выпущенное влево из точки x₃ в момент τ (см. рис. 2); среди таких решений обязательно есть решение, проходящее через точку (t₀, x₀).

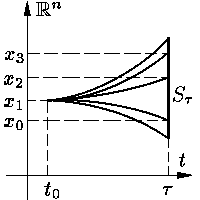
Рис. 2.

Задача О1.3. Докажите теоремы Кнезера и Фукухары в скалярном случае.

В многомерном (даже двумерном) случае доказательство существенно сложнее, в частности потому, что множество S_τ не обязательно выпукло. Например, в двумерном случае оно может быть окружностью.

В условиях теоремы Пеано все решения задачи (1) – (2) продолжимы на отрезок [t₀ – T, t₀ + T] (об этом будет сказано подробнее в очерке О3). Если же не все решения задачи (1) – (2) продолжимы на отрезок [t₀, τ], то в многомерном случае сечение S_τ, а следовательно, и интегральная воронка W_τ, может быть не связной.

Задача О1.4. Подтвердите последнее утверждение примером двумерной системы.

Перейдем к исследованию структуры границы интегральной воронки. В скалярном случае все обстоит просто: при τ ∈ [t₀ – T, t₀ + T] граница интегральной воронки W_τ состоит из двух решений задачи (1) – (2). Доказательство этого факта сводится к проверке того, что функции

xв(t) = sup x∈Wτ {x(t)}, t ∈ [t0, τ]}

и

xн(t) = inf x∈Wτ {x(t)}, t ∈ [t0, τ]}

являются искомыми "граничными" решениями (докажите, воспользовавшись компактностью множества решений). Решения x_в и x_н называются верхним и нижним решениями задачи (1) – (2). Эти решения обладают следующим очевидным свойством (из-за которого они так и называются): для любого x ∈ W_τ

xн(t) ≤ x(t) ≤ xв(t), t ∈ [t0, τ].

(6)

В многомерном случае аналог сформулированного утверждения выглядит следующим образом. Для любой x₁ ∈ ∂S_τ (∂Ω обозначает границу множества Ω: ∂Ω = Ω ∩ CΩ; здесь Ω — замыкание Ω, а CΩ — дополнение Ω) существует решение x задачи (1) – (2) такое, что x(τ) = x₁ и

(t, x(t)) ∈ ∂Ωτ

при всех t ∈ [t₀, τ]. В то же время нельзя утверждать, что для любой точки (t, x₁) ∈ ∂Ω_τ (t₀ < t < τ) найдется решение x такое, что

x(t) = x1 и (s, x(s)) ∈ ∂Ωτ

при всех s ∈ [t₀, τ]. Другими словами, множество {x ∈ W_τ: (t, x(t)) ∈ ∂Ω_τ при всех t ∈ [t₀, τ]} точек графиков решений, целиком лежащих на границе воронки, не исчерпывает, вообще говоря, всей границы воронки Ω_τ.

В заключение скажем несколько слов об аналоге неравенства (6) для систем дифференциальных уравнений. Если понимать неравенство (6) покоординатно (т. е. считать, что две функции x и y на отрезке [a, b] со значениями в Rⁿ связаны неравенствами x(t) ≤ y(t), если имеют место покоординатные неравенства x_i(t) ≤ y_i(t), i = 1, ..., n; t ∈ [a, b]), то без дополнительных ограничений верхнее и нижнее решения задачи (1) – (2), вообще говоря, не существуют. Но если предполагать, например, монотонность функции f по x (что означает выполнение неравенства f_i(t, x) ≤ f_i(t, y) при всех i = 1, ..., n, если x_i ≤ y_i при всех i = 1, ..., n), то тогда в интегральной воронке W_τ существуют верхнее x_в и нижнее x_н решения, т. е. решения, удовлетворяющие (6). Подробнее об этом будет сказано в очерке О2.

Литературные указания. Теорема Пеано и ее варианты излагаются в большинстве учебников по обыкновенным дифференциальным уравнениям (см., напр., [Бибиков, Петровский, Сансоне]). Продвинутое изложение описанного в очерке круга вопросов можно найти в [Коддингтон — Левинсон, Немыцкий — Степанов, Хартман, Hale].

Задачи. О1.5. Пусть выполнены условия теоремы Пеано и n = 1. Надрешением задачи (1) – (2) на [t₀, t₀ + T] называется непрерывно дифференцируемая функция φ: [t₀, t₀ + T] → R такая, что

φ′(t) > f[t, φ(t)] при всех t ∈ [t0, t0 + T],

φ(t0) = x0.

Докажите, что: а) множество надрешений задачи (1) – (2) на отрезке [t₀, t₀ + T] не пусто; б) функция, определенная на t ∈ [t₀, t₀ + T] равенством

ψ(t) = inf{φ(t): φ надрешение},

является верхним решением задачи (1) – (2) на [t₀, t₀ + T] (этот способ доказательства теоремы Пеано предложен Перроном). Введя понятие подрешения, аналогичным способом докажите существования нижнего решения.

В следующих четырех задачах излагается способ доказательства теоремы Пеано, использующий так называемый принцип Шаудера. Этот способ оказывается продуктивным и во многих других задачах. Непрерывный оператор F: Ω → E (здесь E — банахово пространство, Ω — подмножество E) называется вполне непрерывным, если он переводит любое ограниченное подмножество множества Ω в относительно компактное множество. Принцип Шаудера неподвижной точки гласит: любой вполне непрерывный оператор, переводящий непустое замкнутое выпуклое ограниченное подмножество Ω банахова пространства в себя, имеет в Ω по крайней мере одну неподвижную точку, т. е. такую точку x*, что Fx* = x*.

Пусть функция f удовлетворяет условиям теоремы Пеано, а T и b — числа, фигурирующие в этой теореме. Пусть B — шар пространства C([t₀, t₀ + T], Rⁿ) радиуса b с центром в точке φ(t) ≡ x₀. Определим на B оператор F формулой

(Fx)(t) = x0 + ∫ t t0 f[s, x(s)] ds.

О1.6. Докажите, что F: B → C([t₀, t₀ + T], Rⁿ).

О1.7. Докажите, что F(B) ⊆ B.

О1.8. Докажите, что F вполне непрерывен.

О1.9. В силу принципа Шаудера F имеет в B по крайней мере одну неподвижную точку. Докажите, что она является решением задачи (1) – (2).

О1.10. На примере задачи Коши x′ = 2√|x|, x(0) = 0 покажите, что любое ее решение может быть представлено в виде предела последовательности (3).

О1.11. То же самое покажите не для приближений (3), а для приближений Тонелли.

О1.12. Приведите пример задачи Коши, для которой некоторые последовательные приближения не являются сходящимися.

О1.13. Пусть все решения задачи (1) – (2) продолжимы на отрезок [t₀, t₀ + T]. Докажите, что интегральная воронка этой задачи на [t₀, t₀ + T] равномерно ограничена.

О1.14. Докажите, что в условиях предыдущей задачи интегральная воронка компактна в пространстве C([t₀, t₀ + T], Rⁿ). Является ли она компактной в C¹([t₀, t₀ + T], Rⁿ)?

О1.15. Приведите пример задачи Коши, для которой множество S_τ не выпукло.

О1.16. Приведите пример задачи Коши, у которой множество S_τ не является односвязным (например, представляет собой окружность).

В следующих задачах описываются способы доказательства теоремы Коши — Пикара с помощью т. н. принципа сжимающих (или сжатых) отображений. Этот материал скорее относится к § 3.2, однако помещен здесь, чтобы выявить свойства интегрального оператора F. Напомним, что отображение, действующиее в нормированном пространстве называется сжимающим или сжатым, если оно удовлетворяет условию Липшица с константой меньшей единицы. Принцип сжимающих отображений утверждает, что если F — сжимающее отображение на банаховом пространстве E, то F имеет в E единственную неподвижную точку x* (т. е. x* = F(x*)), причем последовательные приближения, начатые в произвольной точке x₀ ∈ E, определяемые рекуррентой формулой x_k+1 = F(x_k), сходятся к x* со скоростью геометрической прогрессии:

||xk – x*|| ≤ CLk,

где C — некоторая (зависящая от x₀) константа, а L < 1 — константа Липшица.

Ниже предполагается, что f: R×Rⁿ → Rⁿ — непрерывен и удовлетворяет условию Липшица с константой K (ср. с условиями теоремы Коши — Пикара).

О1.17. Покажите, что оператор F действует в C([t₀, t₀ + T], Rⁿ).

О1.18. Покажите, что оператор F на C([t₀, t₀ + T], Rⁿ) удовлетворяет условию Липшица с константой L = KT. Следовательно, при T < 1/K оператор F является сжимающим и поэтому, в силу принципа сжимающих отображений имеет единственную неподвижную точку, являющуюся решением задачи Коши (1) – (2).

Таким образом, прямое применение к оператору F принципа сжимающих отображений позволяет доказать только "локальную" версию теоремы Коши — Пикара (T < 1/K). Чтобы доказать глобальный вариант этой теоремы изменим норму в прострагстве C([t₀, t₀ + T], Rⁿ), а именно определим

||x||α =  max t∈[t0, t0+T] eα(t–t0)||x(t)||.

О1.19. Покажите, что при любых T ∈ R и α ∈ R норма || · ||_α эквивалентна исходной норме пространства C([t₀, t₀ + T], Rⁿ).

О1.20. Докажите, что для любого T ∈ R найдется такой α ∈ R, что оператор F является сжимающим относительно нормы ||x||_α в пространстве C([t₀, t₀ + T], Rⁿ).

О1.21. Докажите глобальный вариант теоремы Коши — Пикара.

File based on translation from T_EX by T_TH, version 2.32.
Created 8 Jan 2000, 23:36.
Last modified 20 Apr 2002.