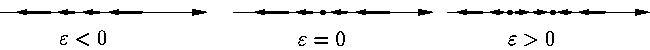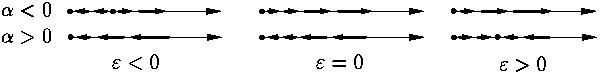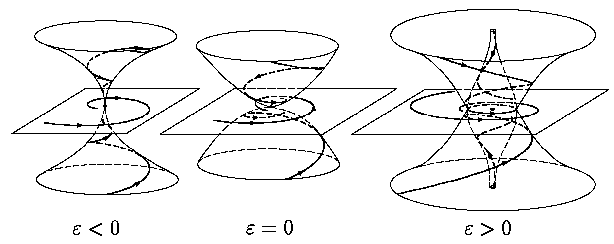§ О16. Бифуркация

Термин бифуркация (букв. раздвоение) употребляется для обозначения качественной перестройки, изменения той или иной картины — в нашем случае фазового портрета обыкновенного дифференциального уравнения при изменении входящего в это уравнение параметра. Простейшим примером может служить, например, изменение фазового портрета системы

d dt ( x1 x2 )   =   ( ε 0 0 –1 ) ( x1 x2 )

при прохождении параметра ε через 0 (см. рис. 1): при ε < 0 фазовый портрет представляет собой устойчивый узел, а при ε > 0 — седло.

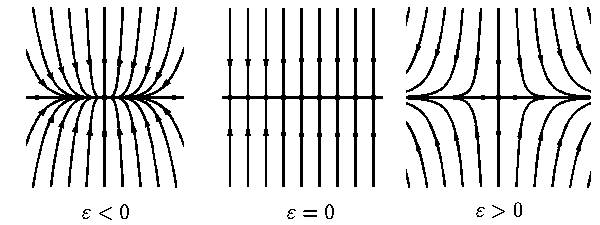
Рис. 1.

Из всего необъятного множества различных бифуркаций мы опишем лишь несколько простейших типов. Поскольку теория бифуркации требует довольно развитой техники, мы как правило не описываем даже идей доказательств.

Начнем с описания локальных бифуркаций состояния равновесия динамической системы. Мы будем рассматривать автономную системы обыкновенных дифференциальных уравнений с параметром вида

x′ = f(x, ε),

(1)

предполагая, что f : Rⁿ×R → Rⁿ — непрерывно дифференцируемая функция. Допустим, что уравнение (1) при ε = 0 имеет стационарную точку x₀: f(x₀, 0) = 0. Будем говорить, что точка ε = 0 является точкой локальной бифуркации динамической системы (1) со стационарной точкой x₀, если найдутся сколь угодно малые значения ε, при которых динамическая система (1) в окрестности точки x₀ не является локально топологически эквивалентной системе, отвечающей нулевому значению параметра.

Допустим, что у матрицы ∂f(x, ε)/∂x)|(x, ε)=(x0, 0) нет собственных значений на мнимой оси. Тогда, в частности, в силу теоремы о неявной функции уравнение

f(x, ε) = 0

(2)

локально однозначно определяет x через ε, т. е. в малой окрестности точки x0 для любого достаточно малого ε найдется единственное решение xε уравнения (2), или, что то же, стационарная точка уравнения (1). Кроме того, поскольку решение xε и матрица A(ε) = ∂f(x, ε)/∂x)|(x, ε)=(x0, 0), а следовательно и ее собственные значения, непрерывно зависят от ε, при малых ε числа n–[A(ε)] собственных значений этой матрицы с отрицательной вещественной частью и число n+[A(ε)] собственных значений этой матрицы с положительной вещественной частью не зависят от ε.

Задача О16.1. Докажите последнее утверждение.

Поэтому из теоремы Гробмана — Хартмана и теоремы о топологической эквивалентности линейных систем вытекает, что при малых ε все динамические системы (1) в окрестности своих стационарных точек x_ε локально топологически эквивалентны, и следовательно, ε = 0 не является точкой бифуркации.

Таким образом, чтобы точка ε = 0 была точкой локальной бифуркации динамической системы (1) со стационарной точкой x₀ необходимо, чтобы матрица A(0) имела хотя бы одно собственное значение на мнимой оси.

Мы рассмотрим только два случая выполнения этого условия: когда A(0) имеет простое нулевое собственное значение и когда A(0) имеет пару простых комплексно сопряженных мнимых собственных значений.

Для иллюстрации первого случая рассмотрим одномерную динамическую систему

x′ = –x2 + ε

(3)

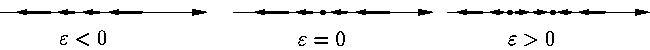
Рис. 2.

(см. рис. 2). При ε < 0 эта система очевидно не имеет стационарных точек. При ε = 0 происходит рождение полуустойчивой стационарной точки, которая при ε > 0 превращается в две — устойчивую и неустойчивую. Эта бифуркация в некотором смысле типична. В многомерном случае соответствующая типичная бифуркация, отвечающая наличию у матрицы A(0) нулевого собственного значения, получается как результат приписывания к уравнению (3) гиперболической системы (рис. 3).

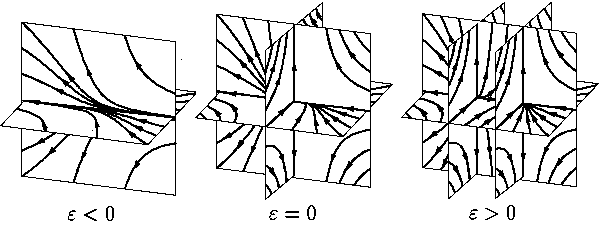
Рис. 3.

Задача О16.2. На примере системы x′1= –x21+ ε, x′2= –x2, x′3= x3 поясните рис. 3.

Задача О16.3. Исследуйте устойчивость и тип стационарных точек системы x′1= –x21+ ε, x′2= –x2. В частности, докажите, что при ε > 0 одна из устойчивых точек обязательно узел, а вторая — седло (которые при ε = 0 сливаются в особую точку, называемую седло-узлом. Кстати, поэтому бифуркацию описанного типа часто называют бифуркацией седло-узла.

Случай наличия у матрицы A(0) пары чисто мнимых комплексно сопряженных собственных значений мы продемонстрируем на примере системы

x′1= εx1 – x2+ αx1(x21 + x22), x′2= x1 + εx2 + αx2(x21+ x22),

(4)

в которой α — вещественный фиксированный параметр (его роль прояснится ниже).

Задача О16.4. Докажите, что система (4) в полярных координатах приводится к виду

ρ′ = ρ(ε + αρ2),    φ′ = 1.

(5)

Второе уравнение в (5) означает, что фазовая точка вращается с постоянной скоростью относительно начала координат. Фазовый же портрет первого уравнения исследуется легко — см. рис. 4).

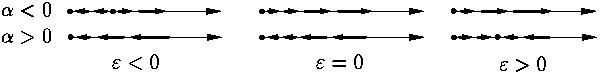
Рис. 4.

Задача О16.5. Обоснуйте рис. рис. 4.

Соответствующие фазовые портреты полной системы (5) (или, что то же самое, системы (4)) изображены на рис. 5. Поясним этот рисунок подробнее. При α < 0 в случае отрицательного ε у динамической системы (4) нуль является экспоненциально устойчивым фокусом. Когда ε обращается в нуль, начало координат продолжает оставаться устойчивым фокусом, правда, уже не экспоненциально устойчивым.

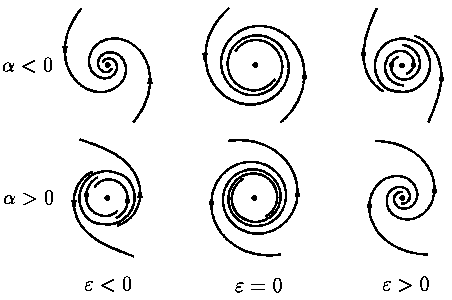
Рис. 5.

Задача О16.6. Докажите последнее утверждение.

Когда ε становится положительным, начало координат теряет устойчивость и одновременно рождается малый предельный цикл динамической системы (4). Начало координат "передает" свою устойчивость этому циклу — он орбитально асимптотически устойчив.

Задача О16.7. Покажите, что амплитуда отвечающего этому циклу решения пропорциональна √ε.

При положительном значении параметра α картина иная. При ε < 0 начало координат представляет собой экспоненциально устойчивое положение равновесия, окруженное неустойчивым предельным циклом (пропорционального √ε радиуса). При ε = 0 этот цикл сливается с началом координат, опять же "передавая" ему свою неустойчивость, причем неустойчивость пока не экспоненциальная. Впоследствии, при ε > 0, начало координат становится экспоненциально неустойчивым фокусом.

Описанная бифуркация носит название бифуркации рождения цикла или бифуркации Пуанкаре — Андронова — Хопфа. Она так же как и бифуркация седло-узла в некотором смысле типична. И опять же в многомерном случае соответствующая типичная бифуркация получается приписыванием к системе (4) гиперболической системы. Один из примеров (отвечающий случаю α < 0) изображен на рис. 6.

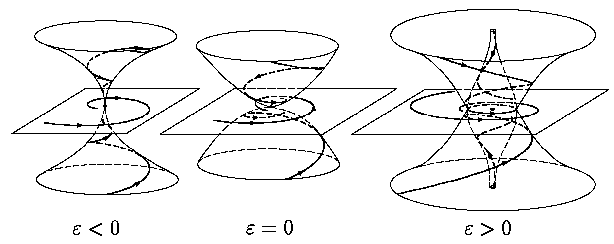
Рис. 6.

Бифуркация рождения цикла, отвечающая случаю α < 0, называется мягким возбуждением автоколебаний, сопровождающим потерю устойчивости стационарной точки, поскольку при возрастании параметра рождающийся цикл непрерывно зависит от ε. В противоположность этому, потеря устойчивости положения равновесия при α > 0 называется жестким возбуждением системы, т. к. фазовая точка, находившаяся при ε < 0 в окрестности устойчивого начала координат, при ε > 0 быстро "выбрасывается" из окрестности стационарной точки (например в окрестность имеющейся у системы удаленной устойчивой стационарной точки или удаленного устойчивого цикла).

В заключение очерка мы приведем несколько рисунков, иллюстрирующих типичные бифуркации предельного цикла динамической системы. Предположим у системы (1) при ε = 0 имеется предельный цикл φ₀ и пусть G — соответствующая ему функция последования. Пользуясь теоремой о неявной функции, можно показать, что если у G′(0) нет единичного мультипликатора (т. е. собственного значения), то при малых ε у системы (1) есть единственный близкий к φ₀ цикл φ_e близкого к периоду цикла φ₀ периода.

Задача О16.8. Докажите!

Кроме того, можно также показать, хотя это уже достаточно сложно, что если у G′(0) нет собственных значений на единичной окружности, то в окрестности цикла φ_e системы (1) при малых ε локально топологически эквивалентны друг другу. Поэтому для бифуркации цикла необходимо наличие мультипликаторов на единичной окружности.

На рис. 7 изображена бифуркация, отвечающая наличию единичного мультипликатора у G′(0). Она в некотором смысле аналогична бифуркации седло-узла.

Рис. 7.

Если у G′(0) есть мультипликатор, равный –1 (и, следовательно, у [G′(0)]² есть мультипликатор, равный +1), то в общем случае возникает так называемая бифуркация удвоения периода. Исходный цикл становится неустойчивым (он изображен на рис. 8 пунктиром), "отдавая" устойчивость рождающемуся циклу периода, близкого к удвоенному периоду исходного

Рис. 8.

На рис. 9 изображена бифуркация цикла, отвечающая наличию у G′(0) пары простых комплексно сопряженных мультипликаторов на единичной окружности. Она аналогична бифуркации рождения цикла и называется бифуркацией рождения инвариантного тора. Вокруг потерявшего устойчивость цикла образуется инвариантное многообразие, гомеоморфное тору. В общем случае на этом торе при приближении параметра к нулевому (бифуркационному) значению в бесконечном числе рождаются и умирают длиннопериодические предельные циклы.

Рис. 9.

Литературные указания. Систематическое описание бифуркаций двумерных динамических систем см. в [ Андронов — Леонтович — Гордон — Майер]. Современное изложение результатов и методов можно найти в [Арнольд, Итоги науки и техники..., Марсден — Мак-Кракен]. Применение теории индекса к исследованию бифуркаций описано в [ Красносельский, Красносельский — Забрейко].

Задачи. О16.9. Является ли точка ε = 0 точкой бифуркации системы x′1= –x1 + x2, x′2= εx1 – x2, x′3= –x3 в окрестности нулевого положения равновесия?

О16.10. Исследуйте бифуркацию при ε = 0 в окрестности нулевой стационарной точки уравнения x′ = x(ε – x²) (это уравнение характеризуется тем, что оно инвариантно относительно симметрии g(x) = –z).

О16.11. Докажите, что сколь угодно малым возмущением правой части уравнения x′ = ε² – x² (т. е. добавлением к правой части равномерно достаточно малой функции f(x)) бифуркацию при ε = 0 в окрестности нулевой стационарной точки можно устранить.

О16.12. Можно ли проделать это с уравнением, фигурирующим в задаче О16.10?

О16.13. Покажите, что устранить точку бифуркации динамической системы (3) малым возмущением нельзя, т. е. при достаточно малом C¹-возмущении системы в окрестности точки ε = 0 всегда есть точка бифуркации.

О16.14. Опишите бифуркацию в динамической системе, описываемой в полярных координатах уравнением ρ′ = ρ(ε – ρ) (2ε – ρ), φ′ = 1.

О16.15. Аналогичный вопрос для системы ρ′ = (ε – ρ² + 2ρ – 1), φ′ = 1.

О16.16. Покажите, что динамическая система, отвечающая уравнению Рэлея x′′ = (x′)³ – εx′ + x = 0 при ε = 0 испытывает бифуркацию рождения цикла.

О16.17. Пусть состояние равновесия линейной двумерной системы x′ = Ax является центром. Приведите пример функции f : R²×R → R² такой, что точка ε = 0 является точкой бифуркации рождения цикла системы x′ = Ax + f(x, ε); не является точкой бифуркации.

О16.18. Приведите пример трехмерной динамической системы, в которой происходит бифуркация рождения инвариантного тора.

О16.19. Исследуйте фазовый портрет системы x′1= x2, x′2= x1 – x21 (воспользуйтесь тем, что функция F(x1, x2) = 2x31– x21+ 3x22 является ее первым интегралом). В частности, покажите, что существует траектория, у которой и α-, и ω-предельные множества совпадают с нулевой стационарной точкой (траектории, у которых совпадающие α- и ω-предельные множества являются стационарными точками или циклами, называются гомоклиническими).

О16.20. На примере системы

x′1= 2x2 – ε (x31 – 6x21 + x22)(12x1 – 3x22), x′2= 12x1 – 3x21+ 2ε (x31 – 6x21 + x22)x2

объясните изображенную на рис. 10 бифуркацию (она называется бифуркацией гомоклинической траектории седла, или бифуркацией петли сепаратрисы седла ).

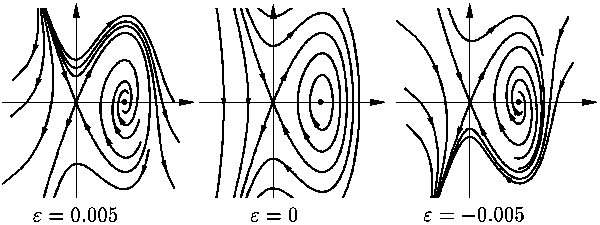
Рис. 10.

File based on translation from T_EX by T_TH, version 2.32.
Created 8 Jan 2000, 12:33.
Last modified 26 Apr 2002.