§ О33. Приближенные методы решения задачи Коши

В подавляющем большинстве случае (или, как еще говорят, в общем положении) нельзя указать точную формулу, позволяющую вычислить значение в любой точке того или иного решения дифференциального уравнения. В то же время исследователю-прикладнику часто нужна именно количественная информация о решении. Поэтому задача построения различных эффективных способов приближенного нахождения решений дифференциальных уравнений весьма актуальна.

Искать приближенные решения, разумеется, можно разными способами. Например, можно искать интегрируемое в квадратурах дифференциальное уравнение, решения которого аппроксимируют решения исходного. Такое уравнение указать, как правило, все-таки трудно. Поэтому можно попытаться искать более простое уравнение, аппроксимирующее решения исходного (см. по этому поводу, в частности, очерки Дифференциальные уравнения с малым параметром при старшей производной, Принцип усреднения и Теория возмущений).

Для отыскания приближенного решения можно воспользоваться также методом последовательных приближений, заменив в нем интеграл (вовсе не обязательно берущийся) какой-либо квадратурной формулой (возможность такой замены требует, конечно, обоснования). Но поскольку этот метод требует большого объема вычислительной работы (на каждой итерации приходится неоднократно вычислять значения правой части уравнения), он играет, в основном, теоретическую роль — например, он полезен при доказательстве теоремы Коши — Пикара или при доказательстве дифференцируемости оператора сдвига.

Можно также пытаться раскладывать искомое решение в степенные или тригонометрические ряды (например, в ряды Тейлора или Фурье). Уравнения на коэффициенты этих рядов получаются из исходного дифференциального уравнения. Эти методы требуют, как правило, большого объема аналитической плохо алгоритмизируемой работы. Например, для нахождения коэффициентов ряда Тейлора решения нужно вычислять производные высоких порядков от правой части уравнения. В силу этого разложения решений в такие ряды пока мало пригодны для практического использования на ЭВМ. Правда, в последнее время появились эффективные пакеты программ для символьных преобразований на ЭВМ; возможно они окажутся полезными в этом направлении.

В настоящее время наиболее универсальными и эффективными методами приближенного решения дифференциальных уравнений являются так называемые конечно-разностные) их еще называют разностными или сеточными) методы, к изложению основ которых мы и переходим. Вводная часть этого очерка относится и к следующему очерку.

Итак, рассматривается (для простоты, скалярное) дифференциальное уравнение

x′ = f(t, x).

(1)

Мы будем искать решение (1), удовлетворяющее начальным или краевым условиям, которые будут записываться в виде

g(x) = 0.

(2)

Например, в случае задачи Коши для уравнения (1), выделяемой начальным условием x(0) = x₀, оператор g имеет вид g(x) = x(0) – x₀. А для краевой задачи

x′′ = φ(t, x, x′),    t ∈ [0, T],

x(0) = x0,    x′(T) = x1,

в которой уравнение приведено к виду (1) заменой переменных y₁ = x, y₂ = x′, оператор g имеет вид g(y₁, y₂) = (y₁(0) – x₀, y₂(T) – x₂).

Запишем теперь задачу (1) – (2) в операторном виде

F(x) = 0,

(3)

где

F(x) = (x′ – f(t, x), g(x)).

Здесь мы не обсуждаем вопрос об области определения и области значений оператора F.

Задачу о приближенном решении уравнения (3), вернее, задачи (1) – (2), мы будем понимать так. Пусть для любого τ > 0 задано множество Mτ точек 0 = t0 < t1 < ... < tk = T, такое, что τ = max1≤i≤k|ti – ti–1|. Множество Mτ называется сеткой, его элементы — узлами, а τ — шагом сетки. Требуется указать функцию xτ: Mτ → Rn (она называется сеточной функцией), которая аппроксимирует в том или ином смысле решение x уравнения (3). Аппроксимация при этом, как правило, понимается в следующем смысле: ||xτ – Pτx|| мала при малых τ; здесь Pτx — сужение точного решения x задачи (3) на Mτ, а ||·|| — какая-либо норма в пространстве Sτ функций на Mτ (обычно, равномерная: ||y|| = max0≤i≤k|y(ti)| или квадратичная: ||y|| = [∑ki=0|y(ti)|2]1/2). Уравнение

Fτ(y) = 0,

(4)

из которого находится сеточная функция x_τ, называется разностной схемой. Обычно считается, что F_τ: S_τ → S_τ. Говорят, что разностная схема (4) сходится с порядком m (или является схемой m-го порядка точности), если при всех достаточно малых τ

||Pτx – xτ|| ≤ Cτm,

где C — не зависящая от τ константа.

В виде разностной схемы может быть интерпретирован известный читателю метод ломаных Эйлера для задачи Коши (т. е. для задачи (3) в случае, когда g(x) = x(0) – x₀). Пусть сетка M_τ равномерная: t_i+1 – t_i = τ, а оператор F_τ: S_τ → S_τ имеет вид

[Fτ(y)]i = { yi – yi–1 τ   –  f(ti–1, yi–1),  если 0 < i < k, yi – x0,  если i = 0;

здесь использовано обозначение y_i = y(t_i). Такая разностная схема называется явной схемой Эйлера. Явной она называется потому, что ее решение (т. е. решение уравнения (4)) в этой ситуации может быть явно вычислено по рекуррентным формулам

y0 = x0,

yi = yi–1 + τf(ti–1, yi–1), i = 1, ..., k.

Единственным отличием метода ломаных Эйлера от явной схемы Эйлера заключается в том, что в первом ищется функция, заданная на [0, T] (ломаная Эйлера), а во втором — сеточная функция (узлы этой ломаной).

Явная схема Эйлера при некоторых естественных предположениях на f обладает двумя важными свойствами, из которых, как мы покажем ниже, будет вытекать, что она является сходящейся с первым порядком.

Во-первых, при достаточно малых τ

||Fτ(Pτx)|| ≤ C1τ,

(5)

где C₁ — константа, не зависящая от τ, а x — как обычно, точное решение задачи (1) – (2). В этом случае говорят, что схема (4) имеет первый порядок аппроксимации на решении. (Если в правой части неравенства (5) стоит C₁τ^m, то, соответственно, говорят о схеме m-го порядка аппроксимации на решении.) Тот факт, что разностная схема обладает аппроксимацией на решении означает, грубо говоря, что при подстановке точного решения дифференциальной задачи в разностную схему мы получаем невязку соответствующего порядка малости по τ. (Было бы идеально, если бы после такой подстановки мы получали в левой части нуль. Известно, что для любого решения любого дифференциального уравнения существует схема точная на этом решении, однако конструктивно в общем случае она не выписывается.)

Задача О33.1. Докажите, что если f непрерывно дифференцируема по t и x, то явная схема Эйлера имеет первый порядок аппроксимации на решении (воспользуйтесь ограниченностью второй производной решения x и разложением

x(ti) = x(ti–1) + τx′(ti–1) + τ2 2 x′′(ti–1 + Φτ)   (0 < Φ < 1).

Во-вторых, если z ∈ S_τ и, кроме того, ||z|| и τ достаточно малы, то уравнение

Fτ(y) = z

(6)

однозначно разрешимо и существует такая не зависящая от малых τ и ||z|| константа C₂, что

||Fτ–1(z)– xτ|| ≤ C2||z||.

(7)

Такое свойство разностных схем называется устойчивостью. Устойчивость разностной схемы означает, что малые возмущения z в начальных данных и правой части разностной схемы (вызванные, например, невозможностью представления точных величин в ЭВМ) приводят к равномерно малому по τ изменению решения (напомним, что xτ — решение невозмущенной системы, а Fτ–1(z)— возмущенной). В следующих четырех задачах описывается план доказательства устойчивости явной схемы Эйлера. Предполагается, что функция f удовлетворяет условиям теоремы Коши — Пикара.

Задача О33.2. Докажите (воспользовавшись тем, что схема Эйлера явная) однозначную разрешимость уравнения (6) при любых z ∈ S_τ.

Задача О33.3. Покажите, что сеточная функция ξ = y – xτ (здесь y = Fτ–1(z)) удовлетворяет уравнениям

ξ0 = z0,

ξi – ξi–1 τ – f(ti–1, yi–1) + f[ti–1, (xτ)i–1] = zi   (i = 1, ..., k).

Задача О33.4. Индукцией по i покажите, что

|ξi| ≤ (1 + τL)i · L + 1 L ||z||,

где L — константа Липшица функции f по x.

Задача О33.5. Докажите, что

||ξ|| ≤ eLT · L + 1 L ||z|| ≡ C2||z||.

Итак, явная схема Эйлера устойчива.

Покажем теперь, что из аппроксимации и устойчивости следует сходимость разностной схемы. Действительно, если разностная схема имеет m-й порядок аппроксимации на решении, то ||Fτ(Pτx)|| ≤ C1τm (см. (5)) и поэтому, в частности, при малых τ мала и ||Fτ(Pτx)||. Следовательно, в силу устойчивости, Fτ–1[Fτ(Pτx)]существует и ||Fτ–1[Fτ(Pτx)]– xτ|| ≤ C2||Fτ(Pτx)||. Но тогда, очевидно,

||Pτx – xτ|| = ||Fτ–1[Fτ(Pτx)]– xτ|| ≤ C2C1τm = Cτm,

что и требовалось. Таким образом, имеет место следующая

Теорема Лакса. Если разностная схема имеет m-ый порядок аппроксимации на решении и устойчива, то она сходится с m-ым порядком.

Эта теорема описывает наиболее распространенный способ доказательства сходимости разностных схем.

Отметим, что если схема не является устойчивой, то наличия аппроксимации в общем случае не достаточно для сходимости (см. задачи O33.9 – O33.13 в конце очерка).

Остальную часть очерка мы посвятим описанию некоторых наиболее распространенных способов построения разностных схем. Особенно важна задача повышения порядка аппроксимации разностных схем.

Попытаемся повысить порядок аппроксимации явной схемы Эйлера следующим образом. В исходном уравнении (1)заменим производную обычным конечно-разностным соотношением, а f(t, x) постараемся аппроксимировать с более высоким порядком. Например, возьмем вместо f(ti–1, yi–1) "среднее направление" между векторами поля направлений уравнения (1) в точках (ti–1, yi–1) (вектор f1 на рис. 1) и (ti, y*i), где y*i — вычисленное по явной схеме Эйлера следующее значение (вектор f2). Интуитивно ясно, что получившееся направление (вектор f3) ближе к "истинно нужному" направлению (вектор f4). Аналитически получившаяся разностная схема, очевидно, записывается в виде

[Fτ(y)]i = { yi – yi–1 τ   –   1 2 [f(ti–1, yi–1) + f(ti, yi–1 + τf(ti–1, yi–1))],  если i = 1,..., k, y0 – x0,    если i = 0 } = 0.

(8)

Рис. 1.

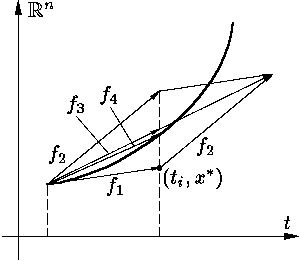
Эту схему, вернее, шаг от значения y_i–1 к y_i записывают обычно в виде двух полушагов

y*i= yi–1 + τf(ti–1, yi–1),

(8а)

yi = yi–1 + τ 2 [f(ti–1, yi–1) + f(ti, y*i)].

(8б)

Поэтому разностная схема (8) носит название предиктор-корректор: на первом полушаге (8а) приближенное решение "предсказывается" (от англ. to predict) с первым порядком точности, а на втором (8б) — "корректируется" (от to correct).

Задача О33.6. Докажите, что если f дважды непрерывно дифференцируема, то схема предиктор-корректор имеет второй порядок аппроксимации на решении.

Описанная схема (так же как и явная схема Эйлера) является представителем обширного класса так называемых разностных схем Рунге — Кутты. Основная идея их построения сводится к сколь можно более точной аппроксимации в разложении (формула Лагранжа)

x(ti) – x(ti–1) = τx′(ti–1 + θτ) = τf[t*, x(t*)]

(здесь t* = t_i–1 + θτ) неизвестной величины f[t*, x(t*)]. Например, весьма популярна схема Рунге — Кутты четвертого порядка (аппроксимации):

yi = yi–1 + 1 6 (C1 + 2C2 + 2C3 + C 4),

где C₁ = f(t_i–1, y_i–1), C₂ = f(t_i–1 + τ/2, y_i–1 + τC₂/2), C₃ = f(t_i–1 + τ/2, y_i–1 + τC₂/2), C₄ = f(t_i, y_i–1 + τC₃).

Схемы Рунге — Кутты являются одношаговыми, поскольку при вычислении значения приближенного решения в точке y_i используется значение приближенного решения только в одной точке y_i–1. Использование дополнительно ранее вычисленных значений в точках t_i–2, t_i–3, ... приводит к так называемым многошаговым разностным схемам. Этот подход к построению разностных схем называется методом Адамса. Его суть сводится к следующему. Заменим в тождестве

x(t+s) – x(t) = ∫ t+s t f[ξ, x(ξ)] dξ

подынтегральное выражение каким-либо интерполяционным полиномом, используя в качестве узлов точки (t_i–2, y_i–2), (t_i–3, y_i–3), ... . Выбор количества точек, интерполяционного полинома, а также точек t и t + s приводит к различным многошаговым схемам.

Несколько иным способом этот подход можно описать на примере трехточечной схемы Адамса — Бэшфорта). Заменим в разложении

x(ti) = x(ti–1) + τx′(ti–1) + τ2 2 x′′(ti–1) + O(τ3)

(9)

значения неизвестной функции x(t_i), x(t_i–1) и ее производных x′(t_i–1) и x′′(t_i–1), соответственно, на y_i, y_i–1, f(t_i–1, y_i–1), [f(t_i–1, y_i–1) – f(t_i–2, y_i–2)]/τ. После отбрасывания в (9) O(τ³) получим

yi = yi–1 + 3τ 2 f(ti–1, yi–1) –  τ 2 f(ti–2, yi–2).

(10)

Рекуррентная формула (10) не позволяет вести вычисления до тех пор пока не заданы y₀ и y₁. Если y₀ и y₁ заданы точно или со вторым порядком точности (по τ), то схема Адамса — Бэшфорта является схемой со вторым порядком аппроксимации. Необходимость вычислять начальные значения с высоким (с соответствующим порядку схемы) порядком точности является основным недостатком многошаговых разностных схем.

Все описанные выше разностные схемы относятся к классу явных разностных схем (значение на следующем шаге может быть вычислено по явным формулам). Простейшим представителем неявных разностных схем является неявная разностная схема Эйлера:

Fy(y) = { yi – yi–1 τ   – f(ti, yi), если i = 1, ..., k  yi – x0,    если i = 0 } = 0.

На каждом шаге она требует решения следующего уравнения относительно неизвестной y_i

yi = yi–1 + τf(ti, yi).

Имеются также "неявные" аналоги схем Рунге — Кутты и Адамса. Разумеется, неявные методы требуют бóльших вычислительных затрат на каждом шаге. Но в общем случае они обладают тем преимуществом, что, как правило, являются безусловно устойчивыми, что по определению означает устойчивость при любых шагах τ; явные же схемы обычно лишь условно устойчивы (устойчивы лишь при малых шагах τ).

Важным и весьма активно развивающимся разделом теории разностных методов решения задачи Коши являются методы решения так называемых жестких систем дифференциальных уравнений. Мы не будем давать точного определения жесткой системы (тем более, что терминология здесь пока не установилась), но приведем типичный пример линейной жесткой системы:

x′1= –λ1x1,

x′2= –λ2x2,

причем, λ₁, λ₂ > 0 и S = λ₁/λ₂ >> 1 (число S называется обычно коэффициентом жесткости системы).

Жесткие системы часто встречаются на практике. Жесткими, как правило, являются (обычно еще и нелинейные) дифференциальные уравнения химической кинетики, обыкновенные дифференциальные уравнения, получающиеся из дифференциальных уравнений гидродинамики дискретизацией по пространственным переменным и т. д. Подчеркнем, что жесткость — это качество дифференциальной системы, а не разностного метода.

Общее решение приведенной выше системы, очевидно, (x2(0)e–λ1t, x2(0)e–λ2t). Поэтому если, например, λ1 ≈ 104, а λ2 ≈ 1, то при t ≥ 10–3 первая компонента решения с точностью e–10 ≈ 5·10–5 равна нулю. В то же время, если мы считаем, к примеру, по явной схеме Эйлера, то для ее устойчивости (см. задачу О33.7 ниже) нужно одновременное выполнение двух неравенств τ ≤ 2λ1–1и τ ≤ 2λ2–1. Поэтому даже вне пограничного слоя на промежутке [10–3, 1] мы вынуждены считать с шагом ≈10–4, а не с шагом ≈1: шаг определяется фактически той компонентой, которая почти равна нулю.

При решении жестких систем оказываются полезными неявные методы, особенно такие их модификации, которые автоматически выбирают шаг в зависимости от поведения решения.

Литературные указания. Данный очерк, как и следующий, относится, скорее, к разделу математики, называемому "Методы вычислений", чем к теории обыкновенных дифференциальных уравнений. Описание приближенных методов решения задачи Коши можно найти почти в каждом учебнике по методам вычислений (см., напр., [Бабушка — Витасек — Прагер, Бахвалов, Годунов — Рябенький, Марчук, Самарский, Современные численные методы..., Хайрер — Нëрсетт — Ваннер].

Задачи. О33.7. Докажите, что явная схема Эйлера для задачи Коши

x′ = ax,   x(0) = x0

(11)

устойчива, если |1 + τa| ≤ 1.

О33.8. Докажите, что неявная схема Эйлера для уравнения (11) безусловно устойчива.

В следующих пяти задачах приводится пример неустойчивой разностной схемы первого порядка аппроксимации на решении, не являющейся вследствие своей неустойчивости сходящейся.

О33.9. Докажите, что если f непрерывно дифференцируема, то семейство разностных схем, зависящих от параметра α ∈ R

Fτ(y) = { α yi – yi–2 2   + (1 – α) yi – yi–1 τ   – F(ti–1, yi–1),    если i = 2, ..., n yi – x0,   если i = 0, 1 } = 0

(12)

имеет первый порядок аппроксимации на решении.

О33.10. Для задачи Коши (11) разностная схема (12) при α = 4 имеет вид

yi = (3 + aτ)yi–1 + 2yi–2,   если i = 2, ..., k,

(13)

yi = x0,   если i = 0, 1.

(14)

Докажите, что уравнение (13) имеет решения вида y_i^j = λ_jⁱ, где λ_j (j = 1,2) — корни уравнения

λ2 – (3 + aτ)λ + 2 = 0.

(15)

(это уравнение называется характеристическим уравнением разностной схемы).

О33.11. Представив решение разностного уравнения (13) в виде y = C₁y¹ + C₂y², найдите коэффициенты C₁ и C₂ так, чтобы выполнялись начальные условия (14). Покажите, что полученное решение — единственное решение разностной схемы (13) – (14).

О33.12. Докажите, что решение y из предыдущей задачи при τ → 0 не сходится к решению дифференциальной задачи (11).

О33.13. Докажите, что разностная схема (13) – (14) неустойчива.

О33.14. Рассмотрим задачу Коши для линейной системы обыкновенных дифференциальных уравнений

x′ = Ax + f(t),   x(0) = x0

(16)

(A: Rⁿ →Rⁿ — линейный оператор). Явную схему Эйлера для (16) запишем в виде

yi = Rτ yi + τfi–1,    если i = 1, ..., k, yi = x0,    если i = 0,

где оператор R_τ: Rⁿ →Rⁿ определяется равенством R_τ = I + τA (такая запись с выделением в левой части y называется каноническим видом разностной схемы, а оператор R_τ в ней — оператором перехода). Докажите, что для устойчивости явной разностной схемы Эйлера для системы (16) необходимо и достаточно равномерной по τ ограниченности степеней оператора перехода: ||R_τⁱ|| ≤ C при всех i = 1, ..., k и достаточно малых τ (константа C, разумеется, не зависит от τ и i).

О33.15. Покажите, что для равномерной по τ ограниченности степеней оператора перехода достаточно выполнения при малых τ неравенства ||R_τ|| ≤ 1 + C₁τ с независящей от τ константой C₁.

О33.16. Докажите, что для выполнения оценки ||R_τ|| ≤ 1 + C₁τ необходимо и достаточно, чтобы все точки спектра оператора R_τ при малых τ лежали в круге радиуса 1 + C₂τ с центром в нуле (C₂ не зависит от τ).

О33.17. Покажите, что разностная схема (13) – (14) не удовлетворяет сформулированному в предыдущей задаче необходимому условию устойчивости (для записи указанной схемы в каноническом виде надо сначала перейти к двухточечной схеме в пространстве S_τ×S_τ заменой z_i = (y_i, y_i–1)).

О33.18. Докажите, что спектр оператора перехода разностной схемы (13) – (14) совпадает со множеством корней характеристического уравнения (15).

О33.19. Обобщите утверждение предыдущей задачи на общие разностные схемы вида

ayi + byi–1 + cyi–2 = fi

(характеристическое уравнение в этом случае имеет вид aλ² + bλ + c = 0).

О33.20. Покажите, что если f дважды непрерывно дифференцируема, то разностная схема

Fτ(y) = { yi – yi–2 2τ   – f(ti–1, xi–1),    если i = 2, ..., k yi – yi–1 τ   – f(t0, x0),   если i = 1 yi – x0,   если i = 0 } = 0

имеет второй порядок аппроксимации.

О33.21. Покажите, что даже если f по-прежнему дважды непрерывно дифференцируема, то в отличие от разностной схемы предыдущей задачи разностная схема

Fτ(y) = { yi – yi–2 τ   – f(ti–1, yi–1),    если i = 2, ..., k   yi – x0,   если i = 0, 1 } = 0

имеет первый порядок аппроксимации на решении. (Эти две задачи показывают, в частности, что важен не только порядок аппроксимации дифференциального оператора, но и порядок аппроксимации начальных условий.)

О33.22. На примере покажите, что явная схема Эйлера для задачи Коши (11) при a < 0 и τa < –2 не сходится.

File based on translation from T_EX by T_TH, version 2.32.
Created 25 Mar 2000, 12:17.
Last modified 3 May 2002.