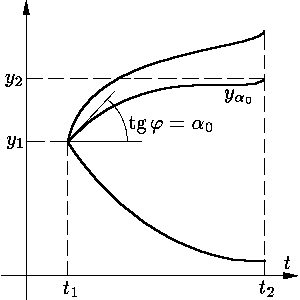§ О24. Краевые задачи

Теорема Коши — Пикара утверждает, что в общем положении для выделения единственного в окрестности точки t₀ решения дифференциального уравнения n-го порядка

y(n) = f(t, y, y′, ..., y(n–1))

достаточно задать в точке t₀ значения неизвестной функции и ее производных до (n – 1)-го порядка включительно, т. е. достаточно задать n чисел

y1 = y(t0), y2 = y′(t0), ..., yn = y(n–1)(t0).

Другими словами, множество решений дифференциального уравнения n-го порядка представляет собой n-параметрическое семейство функций, а задание значений функции и ее производных в одной точке является параметризацией этого семейства. Задача Коши, разумеется, не единственный способ выделения единичных решений (т. е. параметризации множества всех решений). Если значения решения и его производных задавать не в одной, а в двух (или более) точках, то задачи о нахождении таких решений называются краевыми задачами. Из всего многообразия различных видов краевых задач мы рассмотрим в данном очерке лишь один класс задач — так называемую первую краевую задачу (ее также называют иногда задачей Дирихле) для уравнения второго порядка

y′′ = f(t, y, y′),   t ∈[t1,t2],

(1)

y(t1) = y1,    y(t2) = y2;

(2)

здесь f: [t₁, t₂]×R×R → R, t₁ < t₂; y₁, y₂ ∈ R. Решением краевой задачи (1) – (2) называется определенное на [t₁, t₂] решение дифференциального уравнения (1), удовлетворяющее краевым условиям (2).

Задача О24.1. Покажите, что заменой переменных y = x + y₁ + y₂(t – t₁)/(t₂ – t₁) задача (1) – (2) сводится к задаче с нулевыми краевыми условиями.

Естественно начать описание основ теории двухточечной краевой задачи (1) – (2) с линейного случая, т. е. с краевой задачи

y′′ + a1(t)y′ + a0(t)y = b(t),   t ∈ [t1, t2],

(3)

y(t1) = y1,    y(t2) = y2

(4)

(всюду ниже предполагается, что функции a₁, a₂ и b в уравнении (3) непрерывны). Мы также будем рассматривать соответствующее однородное уравнение

y′′ + a1(t)y′ + a0(t)y = 0,    t ∈ [t1, t2],

(5)

и однородные краевые условия

y(t1) = 0,    y(t2) = 0.

(6)

Задача О24.2. Покажите, что описанная в предыдущей задаче замена переменных приводит задачу (5), (4) к задаче (3), (6), а задачу (3) – (4) — к задаче (3), (6) с другой функцией b в правой части уравнения (3).

Таким образом, достаточно изучать краевую задачу (3), (6). Оказывается, однозначная разрешимость задачи (3), (6) при любой функции b ∈ C[t₁, t₂] эквивалентна единственности решения задачи (5) – (6) (т. е. тому факту, что последняя имеет лишь нулевое решение). Действительно, зафиксируем произвольную функцию b ∈ C[t₁, t₂]. Пусть ψ₁, ψ₂ — фундаментальная система решений однородного уравнения (5), а ψ_ч — какое-либо решение неоднородного уравнения (3). Тогда общее решение неоднородного уравнения имеет вид

y(t) = c1ψ1(t) + c2ψ2(t) + ψч(t).

Поэтому задача (3), (6) однозначно разрешима, если (и только если) однозначно разрешима алгебраическая система (относительно неизвестных c₁ и c₂)

c1ψ1(t1) + c2ψ2(t1) + ψч(t1) = 0,

c1ψ1(t2) + c2ψ2(t2) + ψч(t2) = 0.

Таким образом, однозначная разрешимость задачи (3), (6) эквивалентна отличию от нуля определителя

D = ψ1(t1)ψ2(t2) – ψ1(t2)ψ2(t1).

Остается заметить, что неравенство D ≠ 0 эквивалентно отсутствию у задачи (5) – (6) ненулевых решений.

Задача О24.3. Восстановите детали доказательства.

Обозначим через D(L) множество дважды непрерывно дифференцируемых на [t₁, t₂] функций, удовлетворяющих краевым условиям (6) (будем считать, что норма в D(L) индуцируется из C²[t₁, t₂]), а через L — оператор, действующий из D(L) в C[t₁, t₂] по формуле

(Ly)(t) = y′′(t) + a1(t)y′(t) + a0(t)y(t),   t ∈ [t1, t2].

Задача О24.4. Докажите, что: а) оператор L линейный и ограниченный; б) функция L^–1b и только она является решением краевой задачи (3), (6).

Доказанное утверждение можно переформулировать в терминах оператора L так: оператор L: D(L) → C[t₁, t₂] обратим в том и только том случае, если он мономорфен, т. е. имеет лишь тривиальное ядро.

Более интересным и более важным в теории краевых задач оказывается тот факт, что если оператор L обратим, то L^–1 представим в виде

(L–1b)(t) =  ∫ t2 t1 G(t, s)b(s) ds,

(7)

где функция G: [t₁, t₂]×[t₁, t₂] →R, называемая функцией Грина краевой задачи (3), (6), обладает следующими свойствами:

1) G непрерывна;

2) ∂G(t, s)/∂t непрерывна при t₁ ≤ t < s ≤ t₂ и t₁ ≤ s < t ≤ t₂, а на диагонали t = s терпит разрыв типа скачка величины единица:

lim t→s+0 ∂G(t, s) ∂t   –   lim t→s–0 ∂G(t, s) ∂t = 1

при всех s ∈ [t₁, t₂];

3) при всех s ∈ [t₁, t₂] функция t → G(t, s) является решением однородного уравнения (5) на полуотрезках [t₁, s) и (s, t₂];

4) при всех s ∈ [t₁, t₂]

G(t1, s) = 0 и G(t2, s) = 0.

Мы не будем описывать регулярный способ построения функции Грина, применимый и для более общих краевых задач (см. задачи в конце очерка), а воспользуемся спецификой задачи (3), (6) и "угадаем" вид функции Грина. Пусть ψ₁ и ψ₂ — ненулевые решения однородного уравнения (5), причем, ψ₁ удовлетворяет первому, а ψ₂ — второму из краевых условий (6). Будем искать функцию Грина в виде

G(t, s) = { α1(s)ψ1(t) при t1 ≤ t ≤ s ≤ t2, α2(s)ψ2(t) при t1 ≤ s < t ≤ t2.

где α₁ и α₂ — подлежащие определению функции на [t₁, t₂]. Тогда условия 3) и 4) автоматически выполнены при любых непрерывных функциях α₁ и α₂. Условия же 1) и 2) дают следующую систему уравнений для определения этих функций

α2(s)ψ2(s) – α1(s)ψ1(s) = 0,

α2(s)ψ′2(s)– α1(s)ψ′1(s)= 1.

Теперь заметим, что определитель этой системы есть взятый с обратным знаком определитель Вронского системы решений ψ₁, ψ₂, а решения ψ₁ и ψ₂ линейно независимы, т. к. в противном случае они были бы пропорциональны и, следовательно, оба удовлетворяли краевым условиям (6), что противоречит предположению о мономорфности оператора L.

Итак функция G, удовлетворяющая условиям 1) – 4), построена. Докажем равенство (7). Нам нужно показать, что функция

ψ(t) = ∫ t2 t1 G(t, s)b(s) ds

является решением краевой задачи (3), (6). Тот факт, что ψ удовлетворяет краевым условиям (6) очевиден в силу условия 4). Далее, представим ψ(t) в виде

ψ(t) = ∫ t t1 G(t, s)b(s) ds + ∫ t2 t G(t, s)b(s) ds

и, применяя формулу дифференцирования интеграла по параметру, получим

ψ′(t) = ∫ t t1 ∂G(t, s) ∂t b(s) ds + ∫ t2 t ∂G(t, s) ∂t b(s) ds +

+ G(t, t)b(t) – G(t, t)b(t),

ψ′′(t) = ∫ t t1 ∂2G(t, s) ∂t2 b(s) ds + ∫ t2 t ∂2G(t, s) ∂t2 b(s) ds +

+ [G(t, t – 0) – G(t, t + 0)]b(t).

Подставим найденные значения ψ, ψ′ и ψ′′ в уравнение (3):

(Lψ)(t) = ∫ t t1 [ ∂2G(t, s) ∂t2  + a1(t) ∂G(t, s) ∂t  + a0(t)G(t, s) ] b(s) ds +

+ ∫ t2 t [ ∂2G(t, s) ∂t2  + a1(t) ∂G(t, s) ∂t  + a0(t)G(t, s) ] b(s) ds +

+[G(t, t – 0) – G(t, t + 0)]b(t).

В силу условия 3) интегралы равны нулю, а в силу условия 2) последнее слагаемое совпадает с b(t), что и требовалось доказать.

Задача О24.5. Постройте функцию Грина краевой задачи

y′′ = b(t),    y(t1) = 0,    y(t2) = 0.

(8)

Перейдем к исследованию нелинейной краевой задачи (1) – (2). В силу задачи О24.1, не ограничивая общности, можно считать, что в(2) y₁ = y₂ = 0. Пусть

G(t, s) = { (t2 – t)(s – t1) t2 – t1   при  t1 ≤ t ≤ s ≤ t2,   (t – t1)(t2 – s) t2 – t1   при  t1 ≤ s ≤ t ≤t2,

— функция Грина задачи (8) (см. задачу О24.5). Тогда, как нетрудно видеть, решения интегрального уравнения

ψ(t) = ∫ t2 t1 G(t, s)f[s, y(s), y′(s)] ds

и только они являются решениями краевой задачи (1) – (2) (докажите!) Обозначим через C10[t1, t2] пространство непрерывно дифференцируемых на отрезке [t1, t2] функций, удовлетворяющих краевым условиям (2) (напомним, что мы предполагаем равенство y1 и y2 нулю), снабженное нормой

||y||C10= ||y||C + ||y′ ||C .

Определим на C10[t1, t2] оператор F формулой

(Fy)(t) = ∫ t2 t1 G(t, s)f[s, y(s), y′(s)] ds

Легко показывается, что оператор F действует из C10[t1, t2]в C10[t1, t2]. Кроме того, очевидно, неподвижные точки оператора F и только они являются решениями задачи (1) – (2).

Задача О24.6. Докажите последние утверждения.

Если мы теперь укажем условия, при выполнении которых оператор F окажется сжимающим, то в силу принципа сжатых отображений он будет иметь единственную неподвижную точку и, следовательно, задача (1) – (2) будет однозначно разрешима. Простейшим результатом в этом направлении является следующая

Теорема об однозначной разрешимости нелинейной краевой задачи. Пусть функция f: R³ → R непрерывна и удовлетворяет условию Липшица с константой k по второму и третьему аргументам:

|f(t, x1, x2) – f(t, y1, y2)| ≤ k(|x1 – y1| + |x2 – y2|).

Пусть

k [ (t2 – t1)2 8  +  t2 – t1 2 ]  < 1

(9)

Тогда задача (1) – (2) имеет единственное решение.

Для  д о к а з а т е л ь с т в а  достаточно заметить, во-первых, что

∫ t2 t1 |G(t, s)| ds ≤  (t2 – t1)2 8 ,    ∫ t2 t1 | ∂G(t, s) ∂t | ds ≤  t2 – t1 2 .

И, во-вторых, что для любых x, y ∈ C10[t1, t2]

|f[s, x(s), x′(s)] – f[s, y(s), y′(s)]| ≤ k||x – y||C10.

Поэтому, как нетрудно видеть,

||Fx – Fy||C10 ≤ k [ (t2 – t1)2 8  +  t2 – t1 2 ] ||x – y||C10.

Последнее неравенство вместе с условием (9) и означает, что оператор F является сжимающим.

Задача О24.7. Проведите полное доказательство последней теоремы.

Это утверждение допускает различные обобщения. Некоторые из них получаются за счет выбора других норм в пространстве C10[t1, t2](см. задачи в конце очерка).

В заключение опишем еще один распространенный метод исследования краевых задач — так называемый метод стрельбы. Суть его заключается в следующем. Наряду с краевой задачей (1) – (2) рассмотрим задачу Коши

y′′ = f(t, y, y′),    t ∈ [t1, t2],

(2)

y(t1) = y1,    y′(t1) = α,

(11)

в которой α — числовой параметр. Обозначим через yα решение этой задачи. Для разрешимости задачи (1) – (2) необходимо и достаточно наличия такого α0, что yα0(t2) = y2. То есть надо "выстрелить" под таким углом β0 = arctg α0 к "горизонту", чтобы "попасть" в y2. Существование таких α0 можно устанавливать различными способами.

Например, если мы покажем, что функция α → y_α(t₂) непрерывна, а при некоторых α₁ и α₂ выполняются неравенства

yα1(t2) ≤ y2,    yα2(t2) ≥ y2,

(12)

то искомое значение α₀ будет существовать в силу теоремы Больцано — Коши о промежуточном значении непрерывной функции (см. рис. 1). Эта идея реализована в доказательстве следующего утверждения.

Теорема о разрешимости нелинейной краевой задачи. Пусть функция f: R³ → R непрерывна, удовлетворяет условию Липшица по последним двум переменным (с произвольными константами) и ограничена на всей области определения:

|f(t, x, y)| ≤ M.

Тогда задача (1) – (2) имеет по крайней мере одно решение.

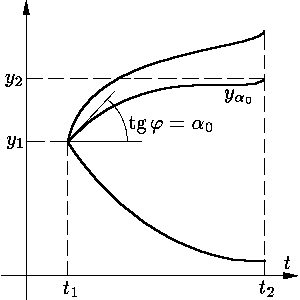
Рис. 1.

Д о к а з а т е л ь с т в о  Во-первых, заметим, что по теореме 4.1.3 о липшицевости оператора сдвига по траекториям уравнения (10) функция α → y_α(t₂) непрерывна.

Далее, докажем, что y_α(t₂) → ±∞ при α → ±∞, чем обеспечим выполнение при некоторых α₁ и α₂ неравенств (12) и, следовательно, разрешимость задачи (1) – (2). Для этого заметим, что на любом решении y_α задачи (10) – (12) выполнено неравенство

|y′′α(t)|= |f[t, yα(t), y′α(t)]| ≤ M,    t ∈ [t1, t2].

Поэтому

α – M·(t2 – t1) ≤ y′α(t)≤ α + M·(t2 – t1),

поскольку

y′α(t)– y′α(t1)= ∫ t t1 y′′α(s) ds.

Аналогично, т. к.

yα(t) – yα(t1) = ∫ t t1 y′α(s) ds.

в силу последних неравенств

y1 + α·(t – t1) – M·(t – t1)(t2 – t1) ≤ yα(t) ≤

≤ y1 + α·(t – t1) + M·(t – t1)(t2 – t1)

и, в частности,

yα(t2) ≥ α·(t2 – t1) + c1,

yα(t2) ≤ α·(t2 – t1) + c2

с очевидными c₁ и c₂. Из этих неравенств вытекает нужное нам соотношение

yα(t2) → ±∞ при α → ±∞.

Теорема доказана.

Литературные указания. Литература по теории краевых задач для обыкновенных дифференциальных уравнений необозрима. Основы теории изложены во многих учебниках (см., напр., [Бибиков, Карташов — Рождественский, Тихонов — Васильева — Свешников, Трикоми, Хартман]).Для углубленного изучения можно рекомендовать [Васильев — Клоков, Гудков — Клоков — Лепин — Пономарев, Кигурадзе, Коддингтон — Левинсон, Красносельский, Красносельский — Забрейко].

Задачи. О24.8. Докажите, что если x и y — решения задачи (5) – (6), z — решение задачи (3), (6), а u — решение задачи (5), (4), то функции c₁x + c₂y, x + z, x + u являются решениями задач (5) – (6); (3), (6) и (5), (4), соответственно.

О24.9. Докажите, что если задача (3), (6) однозначно разрешима при любой функции b ∈ C[t₁, t₂], то найдется такая константа M, что при всех b

||y||C1 ≤ M·||b||C

(здесь y — решение задачи (3), (6)).

О24.10. Пусть в краевой задаче

y′′ + a0(t)y = 0,    y(t1) = y1,    y(t2) = y2

a₀ — непрерывная неположительная функция. Докажите, что данная краевая задача имеет единственное решение при любых y₁ и y₂.

О24.11. Пусть в краевой задаче (3) – (4)

1 4 a21(t) + a0(t) ≤ 0.

Докажите, что эта задача имеет не более одного решения.

О24.12. Рассмотрим краевую задачу

y′′ + a1(t)y′ + a0(t)y = 0,    t ∈ [t1, t2],

(13)

α1y(t1) + β1y′(t1) = y1,    α2y(t2) + β2y′(t2) = y2.

(14)

Пусть α21+ β21> 0, α22+ β22> 0. Докажите, что задача (13) – (14) имеет единственное решение при любых b, y1, y2 в том и только том случае, если соответствующая однородная задача (т. е. задача (13) – (14) с b(t) ≡ 0 и y1 = y2 = 0) имеет только нулевое решение.

О24.13. Определите понятие функции Грина G(t, s) для задачи (13) — (14) (с y₁ = y₂ = 0). Докажите, что если однородная задача имеет только тривиальное решение, то решение задачи (13) – (14) представимо в виде

y(t) = ∫ t2 t1 G(t, s)b(s) ds.

О24.14. Выпишите решение задачи (3) – (4) через функцию Грина задачи (3), (6).

О24.15. Сопряженной к краевой задаче (3), (6) краевой задачей называется задача

z′′ – a1(t)z′ + [a0(t) – a′1(t)]z = p(t),   t ∈[t1, t2],

(15)

z(t1) = 0,   z(t2) = 0

(16)

(разумеется, здесь мы предполагаем дифференцируемость a₁). Пусть y и z — решения уравнений (3) и (15), соответственно. Докажите, формулу Грина

∫ τ2 τ1 [z(s)b(s) – y(s)p(s)]ds = [y′(s)z(s) – y(s)z′(s) + a1(s)y(s)z(s)] | τ2 τ1

для любых τ₁, τ₂ ∈ [t₁, t₂]. В частности,

∫ τ2 τ1 [z(s)b(s) – y(s)p(s)] ds = 0,

если y и z — решения краевых задач (3), (6) и (15) — (16).

О24.16. Докажите, что задача (5) – (6) и сопряженная к ней (однородная) задача (15) – (16) имеют одинаковое число линейно независимых решений.

О24.17. Перенесите утверждения очерка на краевую задачу для системы n дифференциальных уравнений второго порядка вида

y′′ + A1(t)y′ + A0(t)y = B(t),   t ∈ [t1, t2],

(17)

y(t1) = Y1,    y(t2) = Y2,

(18)

где A₁, A₂ — n×n-матрицы с непрерывными на [t₁, t₂] коэффициентами, B: [t₁, t₂] → Rⁿ — непрерывная функция, а Y₁, Y₂ ∈ Rⁿ. Выпишите сопряженную к этой задаче краевую задачу (при условии, что A₁ непрерывно дифференцируема по t). Докажите утверждение задачи О24.9 для краевой задачи (17) – (18).

О24.18. Пусть однородная задача (17) – (18) имеет ровно l линейно независимых решений и пусть y₁, ..., y_l — линейно независимые решения краевой задачи, сопряженной к задаче (17) – (18). Докажите, что задача (17) – (18) с Y₁ = Y₂ = 0 разрешима при тех и только тех B, которые удовлетворяют равенствам

∫ t2 t1 B(s)yi(s) ds = 0 (i = 1,..., l).

О24.19. Пусть функция f в задаче (1) – (2) удовлетворяет условию Липшица с константами k₁ и k₂ по второму и третьему аргументам, соответственно. Докажите, что условие (9) в теореме об однозначной разрешимости нелинейной краевой задачи можно ослабить до условия

k1(t2 – t1)2 8 + k2(t2 – t1) 2 < 1,

если в доказательстве этой теоремы нормировать пространство C10[t1, t2]следующим образом:

||y||C10= max { ||y||, (t2 – t1) 2 ||y′||C } .

О24.20. Рассмотрим нелинейную краевую задачу с малым параметром ε:

y′′ + a1(t)y′ + a0(t)y = εf(t, y, y′),    t ∈ [t1, t2],

(19)

y(t1) = 0,   y(t2) = 0.

(19)

Пусть функции a₁, a₀ и f: [t₁, t₂]×R² → R непрерывны и, кроме того, f удовлетворяет условию Липшица по второму и третьему аргументам. Докажите, что если при ε = 0 задача (19) – (20) имеет единственное решение, то при достаточно малых ε она однозначно разрешима.

О24.21. Докажите теорему о разрешимости нелинейной краевой задачи (1) – (2) применением принципа Шаудера к оператору F, описанному в очерке. Докажите аналог этой теоремы для задачи (19) – (20).

О24.22. Пусть функция f в задаче (1) – (2) непрерывна и строго возрастает по второму аргументу при фиксированных значениях первого и третьего:

f(t, x, y) < f(t, z, y)

при любых t, x < z, y. Докажите, что в этом случае задача (1) – (2) не может иметь более одного решения.

File based on translation from T_EX by T_TH, version 2.32.
Created 19 Mar 2000, 15:01.
Last modified 8 Apr 2002.