§ О36. Дифференциальные уравнения в электро- и радиотехнике

Одной из областей, в которой применение дифференциальных уравнений оказывается наиболее эффективным, является теория электрических цепей. Электрическая цепь представляет собой сеть (если угодно, конечный граф), состоящую из узлов, между которыми включены элементы цепи. Простейшими (и одновременно, важнейшими) элементами электрических цепей являются сопротивления, индуктивности и емкости. Каждый из этих элементов представляет собой двухполюсник, т. е. каждый из них имеет два полюса (вывода, контакта), которыми они присоединяются к узлам цепи. Стандартные их обозначения приведены на рис. 1.

Рис. 1.

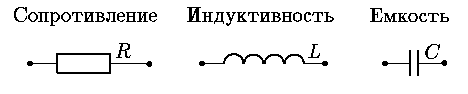
Распределение электрических зарядов в цепи в каждый момент времени в каждом узле создает (электрический) потенциал. Если двухполюсник включен между узлами a и b цепи (такой двухполюсник мы в дальнейшем будем обозначать ab) с потенциалами u_a(t) и u_b(t), то на нем возникает разность потенциалов (падение напряжения) u_ab(t) = u_b(t) – u_b(t). Эта разность потенциалов вызывает движение зарядов через двухполюсник, называемое током. Интенсивность этого движения называется силой тока и обозначается i_ab(t). Ясно, что u_ab(t) = –u_ba(t) и i_ab(t) = –i_ba(t). Разность потенциалов на двухполюснике и сила тока, протекающего через него, не являются независимыми. Они связаны физическими законами, которые с достаточной точностью математически выражаются равенствами (законами функционирования): для сопротивления (индекс _ab ниже опускается)

u = Ri

(1)

(это равенство называют законом Ома), для индуктивностей

u = Li′

(2)

(штрих здесь и ниже означает дифференцирование по t) и для емкостей

i = Cu′.

(2)

Числа R, L и C обозначают (положительные) величины, характеризующие физические свойства соответствующего двухполюсника и также называются сопротивлением, индуктивностью и емкостью.

Задача О36.1. Покажите, что если через индуктивность течет постоянный ток, то разность потенциалов на ней равна нулю, а если разность потенциалов на емкости постоянна, то через нее не течет ток.

Рассчитать электрическую цепь — это значит найти величины токов, протекающих в каждый момент времени через каждый элемент цепи, или, что эквивалентно, указать потенциал в каждом узле цепи в каждый момент времени. Для этого составляется система дифференциальных уравнений, описывающая цепь. Эта система составляется с помощью законов Кирхгофа. Первый закон Кирхгофа гласит: для любого узла цепи сумма всех токов, втекающих в узел изо всех элементов, подключенных к данному узлу, равна нулю. Например, если в цепи имеются только двухполюсники и a₁b, ..., a_kb — все двухполюсники, подключенные к узлу b, то

ia1 b(t) + ... + iak b(t) = 0.

В соответствии со вторым законом Кирхгофа, сумма падений напряжений на всех элементах цепи, включенных в замкнутый контур, равна нулю. При этом замкнутым контуром цепи называется последовательность узлов a₁, ..., a_k такая, что между парами a₁ и a₂, a₂ и a₃, ..., a_k–1 и a_k, a_k и a₁ включены элементы. В частности, в случае цепи из двухполюсников

ua1 a2(t) + ua2 a3(t) + ... + uak–1 ak(t) + uak a1(t) = 0.

Известно (это теорема), что законы Кирхгофа вместе с законами функционирования элементов дают достаточное число уравнений для неизвестных токов и разностей потенциалов на каждом элементе.

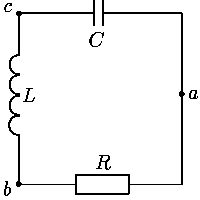
Простейшим примером электрической цепи является колебательный контур (или LRC-цепь), схема которого изображена на рис. 2. В силу первого закона Кирхгофа i_ab(t) = i_bc(t) = i_ca(t); обозначим этот ток через i(t). Далее, по второму закону Кирхгофа

uab(t) + ubc(t) + uca(t) = 0,

(4)

а в силу законов функционирования

uab = Ri,    ubc = Li′,    u′ca = i/C.

(5)

Рис. 2.

Поэтому из (4) и (5)

Ri + Li′ + uca = 0.

Дифференцируя последнее равенство и используя (5), после несложных преобразований, получаем

i′′ + R L i′ + 1 LC i = 0.

Это и есть дифференциальное уравнение, описывающее колебательный контур. Оно полностью совпадает с уравнением линейного осциллятора с трением.

Задача О36.2. Исследуйте работу колебательного контура. Покажите, что в нем могут быть незатухающие колебания в том и только том случае, когда R = 0 (сопротивление отсутствует).

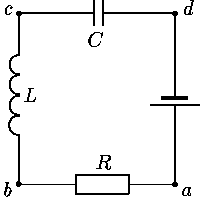
Задача О36.3. Выведите уравнение работы колебательного контура с источником тока (см. рис. 3); здесь ad — новый для нас двухполюсник — источник тока, его закон функционирования: i_ab(t) = e(t), где e(t) — заданная функция времени. Исследуйте функционирование этого колебательного контура в случае, когда e(t) = A·sin ωt (ср. с результатами очерка "Вынужденные колебания линейных систем").

Рис. 3.

Описанные выше элементы цепи в разумном приближении линейны: линейные законы (1) – (3) не учитывают, например, изменения сопротивления R и индуктивности L при их нагревании протекающим через них током, возможности пробоя конденсатора (емкости) и т. п. Кроме того, широко распространены цепи, содержащие элементы, которые по существу не допускают линейного описания.

Одним из таких элементов является электронная лампа — триод. Он представляет собой трехполюсник. Его полюсы (выводы) a, c и g называются, соответственно, анод, катод и сетка (см. рис. 4). Законы функционирования триода с достаточной точностью могут быть описаны соотношениями

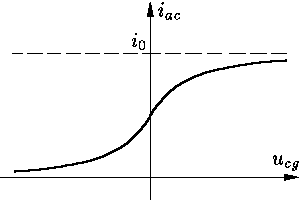
icg(t) = 0,   iac(t) = f[ucg(t)],

(6)

Рис. 4.

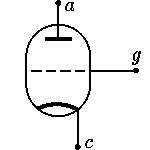
где функция f, называемая вольтамперной характеристикой триода, описывающая зависимость анодного тока i_ac от сеточного напряжения u_cg, задана и зависит от физических характеристик конкретной лампы. В общем случае она имеет вид, изображенный на рис. 5. Мы будем предполагать, что f — гладкая функция с положительной производной, имеющая в нуле точку перегиба, т. е. f ′′(0) = 0, f ′′′(0) < 0.

Рис. 5.

Простейшей и широко распространенной электрической цепью с триодом является ламповый генератор (см. рис. 6). Он представляет собой колебательный контур bdae, связанный с триодом через элемент, называемый взаимоиндукцией. Последний представляет собой четырехполюсник cgdb, состоящий из двух индуктивностей, подчиняющихся следующим законам функционирования

ucg = L1i′cg+ Mi′bd,    ubd = Li′bd+ Mi′cg;

(7)

в них L₁ и L — индуктивности, а M > 0 — коэффициент взаимоиндукции.

Рис. 6.

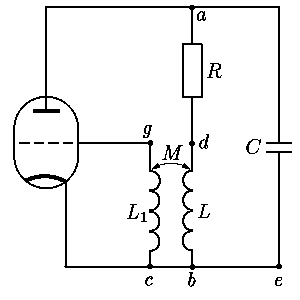
Выведем уравнение, описывающее работу лампового генератора. Первый закон Кирхгофа для узла a дает уравнение

ida – iac = iae,

(8)

а второй закон Кирхгофа для контура aebd — уравнение

ubd + uda + uae = 0.

Подставляя (1) и (2) в последнее равенство, получаем

Li′bd+ Rida + uae = 0.

Однократное его дифференцирование и закон (3) функционирования емкости приводит к уравнению

Li′′bd+ Ri′da+  1 C iae = 0.

(9)

Далее, учитывая отсутствие сеточного тока (см. (6)), из уравнения взаимоиндукции (7) получаем

ucg = Mi′bd

и поэтому

iac = f(Mi′bd).

(10)

Если теперь подставить (10) в (8), а получившееся выражение для i_ae подставить в (9) и, кроме того, обозначить i_bd = i_da = i_ae через i, то мы получим окончательное уравнение

Li′′ + Ri′ + 1 C i = 1 C f(Mi′).

(11)

Задача О36.4. Выпишите соответствующую уравнению (11) систему дифференциальных уравнений первого порядка.

Задача О36.5. Покажите, что при CR < Mf′(0) единственная (нулевая) стационарная точка этой системы является отталкивающей (т. е. асимптотически устойчивой при t → – ∞.

Задача О36.6. Докажите, что любая траектория этой системы ограничена вправо.

Из этих задач, в частности, следует, существование при CR < Mf′(0) отличного от состояния равновесия периодического решения уравнения (11). Действительно, Пусть T_φ — отличная от нулевого состояния равновесия траектория системы, описывающей ламповый генератор. Поскольку она ограничена вправо, ее ω-предельное множество Ω(T_φ) не пусто. Легко видеть, что Ω(T_φ) не может содержать единственную (нулевую) стационарную точку, т. к. она является отталкивающей (докажите это!) Поэтому в силу теоремы Пуанкаре — Бендиксона Ω(T_φ) является циклом. Таким образом при CR < Mf′(0) в ламповом генераторе возникают и поддерживаются незатухающие колебания.

Задача О36.7. (Для знающих радиотехнику). Чем компенсируется в этих автоколебаниях потери энергии на сопротивлении?

Уравнение (11) служит источником различных популярных и важных именных дифференциальных уравнений.

Задача О36.8. Покажите, что заменой i = x + f(0) уравнение (11) приводится к уравнению Рэлея

LCx′′ + F(x′) + x = 0,

где F(x) = RCx – f(Mx) + f(0).

Другое уравнение — уравнение Ван дер Поля — получается из уравнения Рэлея в предположении, что вольтамперная характеристика может быть аппроксимирована кубическим полиномом и члены более высокого порядка в уравнении можно отбросить. Другими словами, предполагается, что

f(x) = f(0) + f ′′(0)x + 1 6 f ′′′(0)x3

(здесь мы используем тот факт, что f ′(0) = 0). Тогда

F(x) = ax – bx3,

причем, a = RC – Mf′(0) < 0 и b = ¹/₆f ′′(0) < 0. Уравнение Рэлея, очевидно, переписывается в виде

LCx′′ + [a – b(x′)2]x′ + x = 0.

(12)

Задача О36.9. Докажите, что заменой t = τ(LC)^1/2, x = y(3b/aLC)^1/2 уравнение (12) переписывается в виде

y′′ + λ[(y′)2 – 1]y′ + y = 0,

в котором λ = – a/(LC)^1/2.

Если теперь последнее уравнение продифференцировать (по τ) и в качестве новой неизвестной функции z взять y′ = dy/dτ, то мы получим собственно уравнение Ван дер Поля

z′′ + λ(z2 – 1)z′ + z = 0

(ср. с очерком Дифференциальные уравнения с малым параметром при старшей производной и задачами О36.15, О36.16 ниже).

Литературные указания. Фактически, ни один учебник по теоретическим основам электро- и радиотехники не обходится без использования дифференциальных уравнений. Описание приложений ОДУ в этих областях встречается также и во многих учебниках по теории дифференциальных уравнений (см., напр., [Андронов — Витт — Хайкин, Боголюбов — Митропольский, Понтрягин, Стокер, Эрроусмит — Плейс]).

Задачи. О36.10. Докажите, уравнения, отвечающие контурам, изображенным на рис. 7а и 7б, экспоненциально устойчивы, а на рис. 7в — устойчиво по Ляпунову.

Рис. 7.

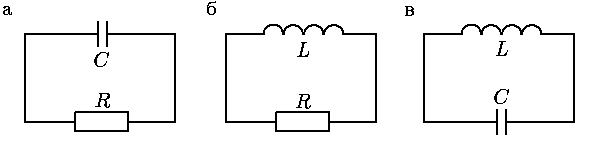
О36.11. Докажите, что уравнение, описывающее колебательный контур экспоненциально устойчиво при R > 0.

О36.12. Рассмотрим колебательный контур с источником тока (см. рис. 3) с источником тока e(t) = A·sin ωt. Найдите резонансную частоту колебательного контура. В частности, покажите, что резонансная частота не зависит от R, а зависит от LC. Поэтому настраивать на резонанс можно только меняя L и/или C (в радиоприемниках для настройки на частоту принимаемой радиостанции обычно используется переменный конденсатор).

О36.13. Пусть мы находимся в условиях предыдущей задачи. Импедансом цепи (в данном случае колебательного контура) называется отношение A/a амплитуды A вынуждающих гармонических колебаний к амплитуде a установившихся гармонических колебаний. Исследуйте зависимость импеданса от ω. В частности покажите, что импеданс минимален при резонансной частоте, а также, что минимум импеданса по частоте стремится к нулю при R → 0.

О36.14. Исследуйте уравнение для тока, текущего через индуктивность, описывающее электрическую цепь, изображенную на рис. 8. Исследуйте для этой цепи вопросы, аналогичные сформулированным в задачах О36.12, О36.13.

Рис. 8.

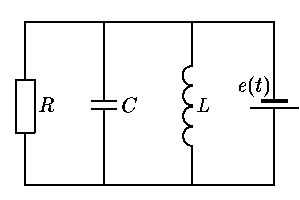
О36.15. Докажите, что замена переменных x₁ = z, x₂ = z³/3 – z + z′/λ, τ = λθ (θ — новое время) преобразует уравнение Ван дер Поля в систему

εx′1= x2 –  x13 3 + x1,

x′2= –x1

с ε = λ^–2.

О36.16. Поясните, опираясь на результаты очерка Дифференциальные уравнения с малым параметром при старшей производной, наличие у уравнения Ван дер Поля при больших λ релаксационных колебаний.

О36.17. Выпишите уравнения, описывающие работу лампового генератора, изображенного на рис. 9. В нем ab — постоянный источник тока: e(t) ≡ e₀ < 0.

Рис. 9.

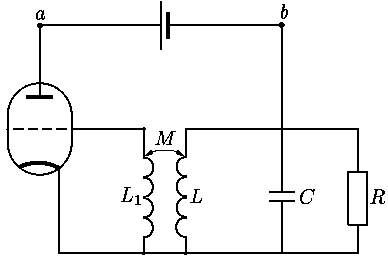
О36.18. Докажите, что в ламповом генераторе, изображенном на рис. 9, возникают и поддерживаются автоколебания, т. е. соответствующее уравнение имеет предельный цикл.

О36.19. (А.А. Андронов). Рассмотрите случай, когда в уравнении (12) вольтамперная характеристика имеет вид

f(x) = { 0 при x > 0, 1 при x ≤ 0.

(Решение уравнения (12) понимается в смысле Каратеодори) Покажите, что в этом случае уравнение (12) имеет единственный предельный цикл, причем этот цикл является орбитально асимптотически устойчивым.

О36.20. Рассмотрим колебательный контур, в котором вместо обычного (линейного) сопротивления включено так называемое нелинейное сопротивление с кубической вольтамперной характеристикой: закон его функционирования имеет вид uab = f(iab) = i3ab/3– iab (см. рис. 10). Выпишите уравнение, описывающее работу этого контура.

Рис. 10.

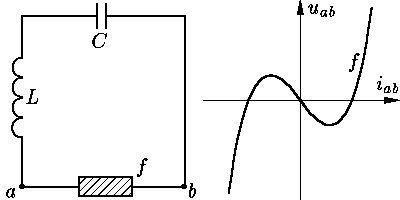
О36.21. Покажите, что при малых L/C в колебательном контуре с нелинейным сопротивлением возникают релаксационные колебания.

File based on translation from T_EX by T_TH, version 2.32.
Created On 27 Mar 2000, 10:41.
Last modified 6 May 2002.