§ О7. Дифференциальные уравнения с разрывной правой частью

Как мы знаем, теорема Пеано гарантирует локальную разрешимость задачи Коши

x′ = f(t, x),    x(t0) = x0

в случае непрерывной функции f. Если функция f непрерывной не является, то утверждение теоремы Пеано в общем случае не верно. Для иллюстрации рассмотрим два важных примера.

Первый пример представляет дифференциальные уравнения, у которых правая часть является "разрывной по t":

x′ = sign t.

(1)

Поле направлений этого уравнения изображено на рис. 1. Очевидно, что задача Коши для уравнения (1), порождаемая начальным условием x(0) = x₀, ни в какой окрестности точки t = 0 решения не имеет: единственным "претендентом" на роль решения является функция x(t) = x₀ + |t|, которая при t = 0 не дифференцируема и, следовательно, не может в этой точке удовлетворять уравнению (1).

Рис. 1.

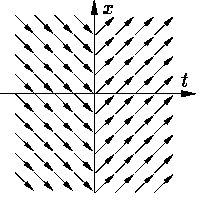
Другая ситуация имеет место для уравнения

x′ = sign x

(2)

(здесь мы предполагаем, что sign 0 = 1). Его поле направлений см. на рис. 2. Задача Коши с начальным условием x(0) = 0 не разрешима (даже локально), поскольку поле направлений, с одной стороне "выгоняет" фазовую точку с множества {(t, x): x = 0} и, в то же время, "возвращает" ее на это множество из любой его окрестности.

Рис. 2.

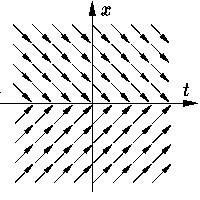
Принципиальное отличие этих двух примеров заключается том, что в первом случае поле направлений заставляет фазовую точку "прошивать" линию разрыва правой части и поэтому она находится на линии разрыва "нулевое время", тогда как во втором случае поле направлений устроено таким образом, что фазовой точке приходится пребывать на линии разрыва неопределенно долгое время.

Дифференциальные уравнения с разрывной правой частью помимо того, что они интересны сами по себе, как математический объект, часто встречаются в механике, электротехнике, теории оптимального управления и других областях науки. Источником дифференциальных уравнений с разрывной правой частью в механике служат, например, механические системы с так называемым сухим трением. Примером такой системы может служить тормозная колодка. Зависимость силы трения от относительной скорости движения колодки качественно имеет вид, изображенный на рис. 3. В электротехнике уравнения с разрывными правыми частями появляются, например, при исследовании цепей, содержащих реле. Реле — это такой элемент цепи, идеализированная зависимость состояния которого от протекающего через реле тока, имеет вид, приведенный на рис. 4.

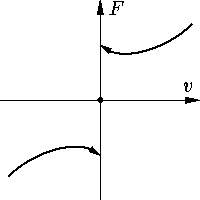Рис. 3.

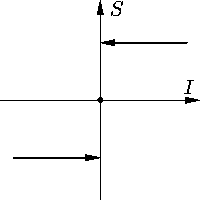Рис. 4.

Таким образом, классическое понятие решения дифференциального уравнения (как функции, обращающей всюду на своей области определения уравнение в тождество) нуждается в обобщении. Разумеется, основным требованием к такому обобщению должно быть условие адекватности процессов, описываемых такими решениями, и соответствующих физических (механических, биологических и т. д.) процессов. По поводу проверки этого требования читателю придется либо поверить нам на слово, либо обратиться к специальной литературе.

Естественно также требовать, чтобы обобщенное решение в точках непрерывности правой части удовлетворяло уравнению в классическом смысле.

В этом очерке от читателя требуется знание основ теории функций действительного переменного, в частности, знакомство с понятиями меры Лебега, измеримой функции, интеграла Лебега.

Мы начнем с более простого случая, когда правая часть дифференциального уравнения

x′ = f(t, x)

(3)

непрерывно зависит от x и может быть разрывной только по t. Тот факт, что в случае непрерывной функции f задача Коши для уравнения (3), порожденная начальным условием

x(t0) = x0,

(4)

эквивалентна интегральному уравнению

x(t) = x0 + ∫ t t0 f(s, x(s)) ds,

(5)

наводит на мысль назвать решением задачи (3) – (4) решение уравнения (5) и в ситуации, когда f разрывна. При этом, поскольку подынтегральная функция в (5) будет "менее непрерывной", естественно понимать интеграл в уравнении (5) в более широком смысле, а именно, в смысле Лебега. Всюду ниже поэтому интеграл и суммируемость понимается как интеграл Лебега и суммируемость по Лебегу.

Один из наиболее известных и распространенных наборов условий на правую часть уравнения (3), при которых такой подход к расширению понятия решения оказывается содержательным в математическом плане и полезным и адекватным в приложениях выглядит следующим образом. Предполагается, что

1) функция x → f(t, x) непрерывна почти при всех t;

2) функция t → f(t, x) измерима при каждом x;

3) существует локально суммируемая функция m: R → R такая, что при каждом фиксированном x почти при всех t выполняется неравенство ||f(t, x)|| ≤ m(t).

Эти условия носят название условий Каратеодори. Они, в частности, гарантируют, что если функция t → x(t) измерима, то функция t → f[t, x(t)] измерима и локально суммируема.

Задача О7.1. Покажите, что функция f(t, x) = (sign sin t^–1)·sin x удовлетворяет условиям Каратеодори.

Решением Каратеодори задачи (3) – (4) на промежутке [t₀ – T, t₀ + T] называют абсолютно непрерывную функцию, удовлетворяющую условию (4) и обращающую почти всюду на [t₀ – T, t₀ + T] уравнение (3) в тождество.

Задача О7.2. Покажите, что если f удовлетворяет условиям Каратеодори, то функция x является решением Каратеодори задачи (3) – (4) в том и только том случае, если x является непрерывным решением интегрального уравнения (5).

Задача О7.3. Покажите, что функция x(t) = x₀ + |t| является решением Каратеодори уравнения (1).

Аналогом теоремы Пеано в данной ситуации является

Теорема Каратеодори. Пусть функция f: R × Rⁿ → Rⁿ удовлетворяет условиям Каратеодори. Тогда задача (3) – (4) на любом промежутке [t₀ – T, t₀ + T] имеет по крайней мере одно решение Каратеодори.

Доказывается эта теорема почти так же, как и теорема Пеано. Поясним, как ее можно доказать, используя, например, приближения Тонелли. Для произвольного натурального k определим на [t₀ – T, t₀ + T] функцию x_k с помощью равенства

xk(t) = x0 при t ∈ [t0 – T, t0]

и рекуррентного (по i) соотношения

xk(t) = x0 + ∫ t t0 f [ s, xk ( s –  1 k ) ] ds при t ∈ [ i – 1 k , i k ]

(6)

(i = 1, ..., [T/k] + 1; здесь [a] — целая часть числа a). В силу условий Каратеодори, как отмечалось выше, подынтегральная функция в (6) измерима и суммируема, так что интеграл в правой части соотношения (6) имеет смысл. Далее, если положить

M(t) = ∫ t t0 m(s) ds,

то, по-первых,

||xk(t)|| ≤ ||x0|| + ∫ t t0 || f [ s, xk ( s – 1 k ) ] || ds ≤

≤ || x0 || + M(t0 + T)   (t ∈ [t0, t0 + T])

(7)

и, во-вторых,

||xk(t) – xk(τ)|| ≤ ∫ t τ || f [ s, xk ( s – 1 k ) ] || ds ≤ | ∫ t τ m(s) ds | =

= |M(t) – M(τ)|   (t, τ ∈ [t0, t0 + T]).

(8)

Условие (7) означает, что семейство функций {xk} равномерно ограничено. А из оценки (8) вытекает, поскольку функция M как интеграл от суммируемой функции непрерывна, и следовательно, равномерно непрерывна, что семейство {xk} равностепенно непрерывно. Поэтому по теореме Арцела — Асколи существует равномерно сходящаяся к некоторой непрерывной на [t0 – T, t0 + T] функции φ подпоследовательность xkm. Остается заменить в (6) k на km и перейти при каждом t ∈ [t0, t0 + T] в получившемся равенстве к пределу при m → ∞. Тогда φ будет решением уравнения (5), а вместе с этим и решением Каратеодори задачи (3) – (4) на [t0, t0 + T]. На промежутке [t0 – T, t0] решение строится аналогично.

Задача О7.4. Покажите, что условия Каратеодори обеспечивают возможность описанного предельного перехода.

На дифференциальные уравнения, удовлетворяющие условиям Каратеодори, переносится большинство утверждений качественной теории обыкновенных дифференциальных уравнений (см. задачи в конце очерка).

Перейдем теперь к уравнениям с "разрывной по x правой частью".

Задача О7.5. Покажите, что уравнение (2) не имеет решения Каратеодори, удовлетворяющего начальному условию x(0) = 0.

Основные идеи мы будем пояснять на простом классе скалярных уравнений, а именно, будем предполагать, что в уравнении (3) функция f: R×R → R непрерывна всюду, за исключением, быть может, множества S, являющегося непрерывной кривой без самопересечений. Будем считать также, что на этой кривой функция f может терпеть разрыв только первого рода: f(t, x) при стремлении (t, x) к (t₀, x₀) ∈ S "с одной стороны кривой S" имеет конечный предел. Три основных возможных ситуации изображены на рис. 5. Вообще говоря, неадекватную, но наглядную картинку дает образ тяжелого шарика, катящегося по поверхности с изломами (см. рис.)

Рис. 5.

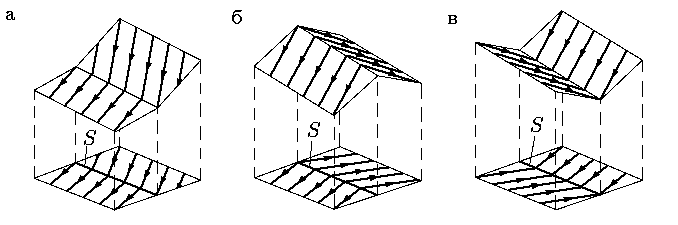
В случае а) интегральные кривые "прошивают" кривую S за "нулевое время". Поэтому в этом случае можно обойтись решениями Каратеодори. Такое решение не будет дифференцируемым только в изолированных точках, а именно, в момент, когда (t, x(t)) ∈ S.

В случае б), даже если поле направлений на S устроено таким образом, что фазовая точка может двигаться по кривой S, это движение не устойчиво в том смысле, что сколь угодно малые возмущения уводят точку из окрестности этой кривой.

Наконец, в случае, изображенном на рис. 5в), траектории, начинающиеся в окрестности кривой S всегда попадают в конце концов на S. В дальнейшем фазовая точка, очевидно, может двигаться только по кривой S. Поэтому поле направлений на кривой разрыва должно быть пере- или доопределено, чтобы движение вдоль этой кривой (это движение называется скользящим режимом) было возможным.

Большинство известных способов переопределения поля направлений на кривой разрыва укладываются в следующую схему. Для каждой точки (t, x) определим некоторое множество F(t, x) вещественных чисел (в результате получится отображение из R×R во множество 2^R всех подмножеств вещественной оси — такие отображения называются многозначными). Наряду с уравнением (3) рассмотрим следующее уравнение — или еще говорят — дифференциальное включение

x′ ∈ F(t, x).

(9)

Решением дифференциального включения (9) на отрезке [a, b] называют абсолютно непрерывную функцию φ: [a, b] → R, для которой почти всюду на [a, b] производная φ′(t) принадлежит множеству F[t, φ(t)]. В такой ситуации решением дифференциального уравнения (3) с разрывной правой частью называют решение дифференциального включения (9).

Подчеркнем, что мы не требуем, чтобы решение было дифференцируемым в каждой точке своей области определения и чтобы оно в каждой точке удовлетворяло включению (9). Многочисленные примеры практики показывают плодотворность такого ослабления понятия решения.

Одна из возможных процедур построения многозначного отображения f состоит в следующем. Для любых (t, x) ∈ R×R обозначим через F₁(t, x) множество предельных значений функции f в точке (t, x):

F1(t, x) = {α:  ∃ (tk → t, xk → x при k → ∞) [α = lim k→∞ f(tk, xk)]}.

Многозначное отображение F определим равенством

F(t, x) = co F1(t, x);

здесь co F₁(t, x) обозначает выпуклую замкнутую оболочку множества F₁(t, x), т. е. минимальное выпуклое замкнутое множество, содержащее F₁(t, x) — в нашем случае вещественнозначной функции f, очевидно, co F₁(t, x) представляет собой отрезок. Очевидно также, что F(t, x) состоит из одной точки f(t, x), если функция f в точке (t, x) непрерывна.

Задача О7.6. Как выглядит отображение F, если f(t, x) = sign (x·sin t)?

Построенное нами многозначное отображение в большинстве встречающихся на практике случаев обладает двумя важными свойствами, гарантирующими разрешимость задачи Коши для дифференциального включения (9) и, автоматически, разрешимость в описанном выше смысле задачи Коши для дифференциального уравнения (3) с разрывной правой частью. Это, во-первых, тот факт, что множество F(t, x) при каждом t и x выпукло, замкнуто и ограничено и, во-вторых, отображение F непрерывно в некотором специальном смысле, а именно, в каждой точке (t₀, x₀) множество F(t, x) содержится в сколь угодно малой окрестности множества F(t₀, x₀), если (t, x) достаточно близка к (t₀, x₀) (это свойство многозначного отображения F называется полунепрерывностью сверху).

Задача О7.7. Докажите, что (однозначное) отображение φ: Rⁿ → Rⁿ, рассматриваемое как многозначное, полунепрерывно сверху в том и только том случае, когда φ непрерывно.

Задача О7.8. Докажите, что многозначное отображение Φ: Rn → 2Rn с замкнутыми образами (Φ(x) замкнуто при любом x ∈ Rn) полунепрерывно сверху, если и только если его график Γ = {(x, y) ∈ Rn × Rn: y ∈ Φ(x)} замкнут в Rn×Rn.

Задача О7.9. Пусть функция f: R×R → R удовлетворяет описанным выше условиям, т. е. непрерывна всюду, за исключением, может быть, кривой S, на которой f может терпеть разрыв первого рода. Докажите, что построенное выше многозначное отображение F полунепрерывно сверху.

Основу теории дифференциальных включений составляет следующая теорема о разрешимости задачи Коши:

Теорема Зарембы. Пусть многозначное отображение F: R × R → 2^R с выпуклыми замкнутыми образами полунепрерывно сверху и ограничено (существует M такое, что |y| ≤ M при всех y ∈ F(t, x) и t, x ∈ R). Тогда задача Коши для дифференциального включения (9), порожденная начальным условием

x(t0) = x0,

(10)

имеет по крайней мере одно решение на любом промежутке вида [t₀, t₀ + T].

Эту теорему можно доказывать различными способами. Мы покажем как ее можно доказать, используя аналог ломаных Эйлера Для любого натурального k положим hk = T/k, tik = t0 + ihk (i = 0, ..., k) и определим ломаную Эйлера xk для дифференциального включения (9) как кусочно линейную функцию на [t0, t0 + T] с точками излома tik (i = 0, ..., k), у которой тангенс угла наклона i-го звена (i = 1, ..., k) равен какому либо числу из множества F[tki–1,xk(tki–1)]. Таким образом,

x′k(t)∈ F[tik,xk(tik)] при t ∈ (tik, tki+1).

(11)

Из ограниченности отображения F, очевидно, вытекает оценка

|x′k(t)|≤ M при t ∈ [t0, t0 + T];

в точках излома под x′_k(t) понимается правая и левая производные. Из этой оценки и условия (10) следуют, как нетрудно видеть, неравенства

|xk(t)| ≤ |x0| + MT,    |xk(t) – xk(τ)| ≤ M |t – τ|    (t, τ ∈ [t0, t0 + T]),

означающие равномерную ограниченность и равностепенную непрерывность семейства функций {x_k}. Поэтому в силу теоремы Арцела — Асколи, не ограничивая общности можно считать, что последовательность {x_k} равномерно сходится к некоторой непрерывной на [t₀, t₀ + T] функции φ. Остается доказать, что в (11) можно перейти к пределу при k → ∞ и что в результате получается соотношение

φ′(t) ∈ F(t, φ(t)) почти всюду на [t0, t0 + T].

(12)

План доказательства последнего утверждения приводится в следующих четырех задачах.

Задача О7.10. Покажите, что функция φ удовлетворяет условию Липшица с константой M и, следовательно, почти всюду дифференцируема.

Задача О7.11. Докажите, что если ψ: [a, b] → R — абсолютно непрерывная функция, то

1 τ [ψ(t + τ) – ψ(τ)] ∈ co D,

где D — множество значений производных функции ψ во всех точках отрезка [t, t + τ] ⊂ [a, b], в которых она существует.

Задача О7.12. Докажите, что

1 τ [xk(t + τ) – xk(t)] ⊂ ∪ s ∈[t–hk, t+τ+hk] F[s, xk(s)]

при всех достаточно больших k.

Задача О7.13. Докажите соотношение (12).

В построенной на основе описанного приема теории дифференциальных уравнений с разрывной ("по x") правой частью имеют место аналоги многих утверждений стандартной теории обыкновенных дифференциальных уравнений (см. задачи в конце очерка).

Литературные указания. Теорию уравнений с "разрывной по t правой частью" можно найти, напр. в [Коддингтон — Левинсон, Сансоне]. Современному состоянию теории уравнений с разрывной правой частью полностью посвящена книга [Филиппов]. Основной поставщик задач в этой области — теория нелинейных колебаний и теория автоматического регулирования (см. [Андронов — Витт — Хайкин, Гелиг — Леонов — Якубович, Неймарк, Уткин]). Новый раздел теории — это так называемые системы с гистерезисными нелинейностями [Красносельский — Покровский].

Задачи. О7.14. Докажите, что функция f(t, x) = A(t)x + b(t), в которой A(t) — m×m-матрица-функция, а b(t) — m-мерная вектор-функция, удовлетворяет условиям Каратеодори в том и только том случае, если все компоненты матрицы A и вектор-функции b локально суммируемы.

О7.15. Перенесите утверждения § 3.1 на линейные системы с локально суммируемыми коэффициентами.

О7.16. Пусть функция f удовлетворяет условиям Каратеодори и обобщенному условию Липшица с локально суммируемой функцией M. Докажите, что задача (3) – (4) имеет на любом отрезке, содержащем точку t₀, в точности одно решение.

О7.17. Докажите, что в условиях задачи О7.16 корректно определен оператор сдвига по траекториям уравнения (3).

О7.18. Докажите, что в условиях теоремы Каратеодори множество решений задачи (3) – (4) компактно в C[t₀, t₀ + T].

О7.19. Докажите, что в условиях теоремы Каратеодори каждое решение задачи (3) – (4) продолжимо до максимального определенного на всей оси.

О7.20. Сформулируйте докажите теорему о нестрогих дифференциальных неравенствах с производными числами в случае, когда f удовлетворяет условиям Каратеодори.

О7.21. Сформулируйте и докажите какое-нибудь содержательное утверждение о непрерывной зависимости решений Каратеодори от параметра.

В следующих трех задачах предполагается, что f: R → R — функция, имеющая в точке x* ∈ R разрыв первого рода и удовлетворяющая условию Липшица на каждом из множеств (–∞, x*) и (x*,+∞). Пусть φ: [t₀, t₀ + T] → R — решение задачи Коши

x′ = f(x),    x(t0) = x0

(13)

(в описанном в очерке смысле).

О7.22. Докажите, что решение задачи (13) единственно, если f(x* + 0) < 0 или f(x* – 0) > 0. Покажите,что если f(x* + 0) > 0 и f(x* – 0) < 0, то решение может быть неединственным.

О7.23. Докажите, что если f_k: R → R — последовательность удовлетворяющих условию Липшица функций таких, что при некотором M и всех k ∈ N₊

|fk(x) – f(x)| ≤   1 k  при |x – x*| ≥   1 k

и

|fk(x)| ≤ M при |x – x* | ≤ 1 k ,

а φ_k: [t₀, t₀ + T] → R — последовательность (классических) решений задачи Коши

x′ = fk(x),    x(t0) = x0,

то

sup t∈[t0, t0+T] |φk(t) – φ(t)| → 0  при   k → ∞.

(14)

О7.24. Рассмотрим следующую задачу Коши для дифференциального уравнения с запаздывающим аргументом:

x′(t) = f [ t, x ( t – 1 k ) ] , t ∈ [0, T],

(15)

x(t) = x0,    t ∈ [ t0 – 1 k , t0 ] .

(16)

Ее решением будем называть абсолютно непрерывную функцию φ_k: [t₀ – 1/k, t₀ + T] → R, удовлетворяющую (16) и обращающую (15) в тождество почти всюду на [t₀, t₀ + T]. Докажите, что задача (15) – (16) разрешима. Покажите, что φ_k удовлетворяет предельному соотношению (14).

О7.25. Докажите, что в условиях теоремы Зарембы каждое решение задачи (9) – (10) может быть продолжено до определенного на всей оси максимального решения.

О7.26. Пусть f: R →2^R — многозначная функция, определяемая равенством

f(x) = { {1} при t ≥ 1, {–1, 1} при t ∈ (–1, 1), {–1} при t ≤ –1.

Докажите, что множество равномерных пределов последовательностей решений задачи Коши

x′ ∈ f(x),    x(0) = 0

на отрезке [0, T] совпадает со множеством решений задачи Коши

x′ ∈ F(x), x(0) = 0,

где F(x) = co f(x).

О7.27. Докажите, что если g: Rn → R — непрерывная положительная функция, а F: Rn → 2Rn, то множество траекторий (подчеркнем, траекторий, а не интегральных кривых) включения

x′ ∈ F(x)

совпадает со множеством траекторий включения

x′ ∈ g(x)F(x)

и, наоборот. (Здесь под g(x)F(x) понимается, как обычно, множество {y ∈ Rⁿ: y = g(x)z, где z ∈ F(x)}).

О7.28. Пусть F: R×R → 2R — полунепрерывное сверху многозначное отображение с выпуклыми замкнутыми образами. Каждой функции x ∈ C[t0, t0 + T] поставим в соответствие множество абсолютно непрерывных на отрезке [t0, t0 + T] функций y таких, что y′(t) почти при всех t ∈ [t0, t0 + T] лежит во множестве F[t, x(t)]. Таким образом определен действующий из C[t0, t0 + T] в 2C[t0, t0+T] многозначный оператор F (он называется многозначным интегральным оператором, порожденным функцией f). Любая точка, лежащая в своем образе при отображении F, т. е. такая, что x ∈ F(x), называется неподвижной точкой многозначного отображения F. Докажите, что задача (9) – (10) эквивалентна задаче о неподвижных точках отображения F (ср. задачей О1.9).

О7.29. Покажите, что в условиях предыдущей задачи оператор F полунепрерывен сверху, его образы выпуклы и замкнуты и он вполне непрерывен в следующем смысле: для любого ограниченного множества Ω ⊂ C[t₀, t₀ + T] множество F(Ω) = ∪_{x ∈ Ω}F(x) относительно компактно в C[t₀, t₀ + T]. (Теперь воспользовавшись теоремой Гликсберга: любое полунепрерывное сверху вполне непрерывное многозначное отображение с выпуклыми замкнутыми образами, переводящее выпуклое замкнутое ограниченное подмножество банахова пространства в себя, имеет по крайней мере одну неподвижную точку, можно доказать теорему Зарембы).

File based on translation from T_EX by T_TH, version 2.32.
Created On 16 Jan 2000, 21:44.
Last modified 23 Apr 2002.