


| § О6. Уравнения, не разрешенные относительно старшей производной | 
|
Если кто-либо двусмысленно сформулировал иск или выступление на суде, то следует принять (такое толкование), которое является для него более полезным.
Дигесты Юстиниана
Для простоты и наглядности мы рассмотрим скалярное обыкновенное дифференциальное уравнение
первого порядка,
| F(t, x, x′) = 0, | (1) |
где F: R3 →
R — непрерывная функция. Напомним, что функция
φ:
Чтобы понять, что представляет собой начальная задача для уравнений, не разрешенных относительно производной, начнем с простейшего примера. Уравнение
| (x′)2 – 1 = 0 | (2) |
очевидно эквивалентно совокупности двух обыкновенных дифференциальных уравнений в нормальной форме
| x′ = 1 | (2а) |
и
| x′ = –1. | (2б) |
Множество интегральных кривых
уравнения (2) представляет собой объединение множеств интегральных кривых
уравнений (2а) и (2б)
(см.
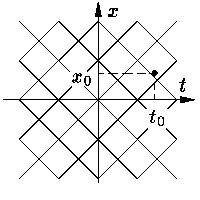
Применительно к уравнению (1) эти же рассуждения выглядят так. Возьмем произвольные t0 и x0. Допустим уравнение
| F(t0, x0, p) = 0 |
(относительно p) разрешимо. Обозначим через p0 один из его корней
(см.
| x(t0) = x0, x′(t0) = p0. | (3) |
Подчеркнем, что в (3) p0
не произвольно, а удовлетворяет соотношению
Будем всюду ниже предполагать, что функция F непрерывно дифференцируема на
R3. Точка
| F′p(t0, x0, p0) ≠ 0. |
Теорема существования и единственности решения задачи (1),
(3).
Для д о к а з а т е л ь с т в а достаточно заметить, что в силу
регулярности точки
| x′ = f(t, x), | (4) |
| x(t0) = x0. | (5) |
Однозначная же разрешимость задачи (4) – (5)
следует из локальной теоремы
Задача О6.1. Восстановите детали доказательства.
Доказанная теорема, по существу, утверждает, что расширенным фазовым пространством для
уравнения (1) является множество (многообразие) S. Для понимания
геометрического смысла уравнений, не разрешенных относительно старшей производной, весьма полезной
оказывается трактовка уравнения (1) как
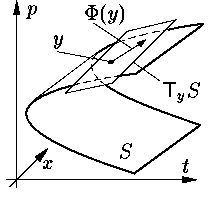
дифференциального уравнения на многообразии Предположим S является гладким
двумерным многообразием, вложенным в R3 (для этого достаточно,
например, чтобы на S полный дифференциал функции F был отличен от нуля).
Уравнение (1) задает на S
векторное поле Φ:
| y′ = Φ(y) | (6) |
на многообразии S, а начальное условие (3) — как условие
| y(t0) = y0 ( = (t0, x0, p0)). | (7) |

Современная терминология здесь такова. Пространство
R3 с координатами (t, x, p)
называется пространством 1-струй функции
x(t) (1-струя функции
x(t) в точке
Задача О6.2. Пусть (t0, x0,
p0) — регулярная точка. Докажите, что если
Задача О6.3. Докажите, что в окрестности регулярной
точки интегральные кривые уравнения
(6) при проектировании на плоскость t0x
параллельно оси 0p переходят в интегральные кривые уравнения (1)
(см.
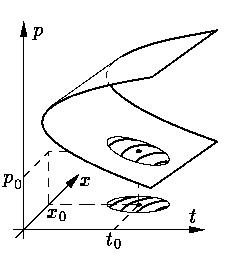
Подчеркнем еще раз, что задание дополнительного начального условия
Таким образом, единственность полученного решения задачи
| F(t, x, p) = 0, Fp′(t, x, p) = 0. |
В общем случае это множество представляет собой кривую на
многообразии S и называется криминантой
уравнения (1). Ее проекция D на плоскость t0x
параллельно оси 0p называется дискриминантной кривой
уравнения. Единственность решения задачи
Задача О6.4. Пусть
| (x′)2 = x. | (8) |
Единственно ли решение соответствующей задачи Коши? Аналогичный вопрос для уравнений
| (x′)3 = x. |
и
| (x′)2 = t. | (9) |
Интегральные кривые уравнений
(8) и (9) и интегральные
кривые соответствующих уравнений на многообразии S изображены на
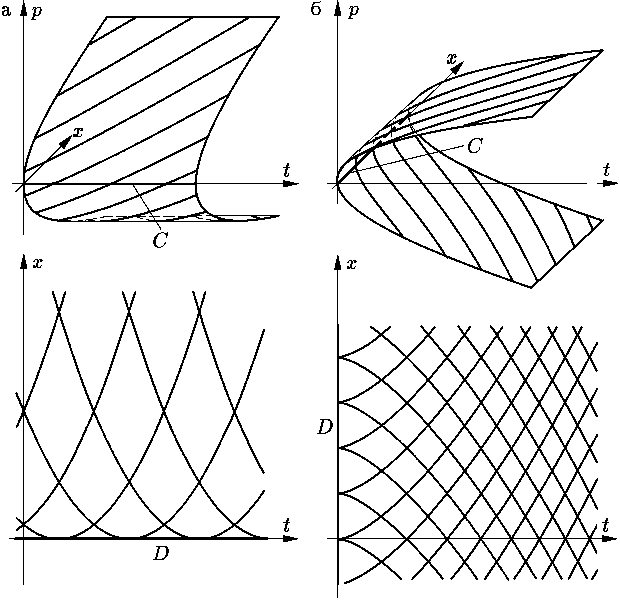
Задача О6.5. Опишите множества всех решений уравнений (8) и (9).
Решение φ: D(φ)
→ R уравнения (1), в каждой точке которого
нарушается его локальная единственность называется особым;
нарушение локальной единственности здесь означает, что в любой окрестности точки
Задача О6.6. Докажите, что дискриминантная кривая уравнения (8) является особым решением, а уравнения (9) — нет.
Задача О6.7. Найдите дискриминантную кривую уравнения
| (x′)2 – (t + x)x′ + tx = 0. |
Является ли она интегральной кривой, отвечающей особому решению?
Если удается найти интеграл
| Φ(t, x, C) = 0 |
уравнения (1), то огибающая семейства кривых (см. курс математического анализа), определяемых этим интегралом (если она существует) является особым решением.
Задача О6.8. Докажите это утверждение.
Несколько слов о методах интегрирования дифференциальных уравнений, не разрешенных
относительно производной. Наиболее распространенным приемом интегрирования является
параметризация уравнения. Допустим двумерное многообразие
| t = Φ(ξ, η), x = Ψ(ξ, η), p = Ξ(ξ, η), | (10) |
| F[Φ(ξ, η), Ψ(ξ, η), Ξ(ξ, η)] ≡ 0, (ξ, η) ∈ D. | (11) |
Тогда соотношение dx = p·dt переписывается в виде
| Ψ′ξdξ + Ψ′η dη = Ξ·(Φ′ξ dξ + Φ′η dη). | (12) |
Теперь если уравнение (12) (рассматриваемое, например, в симметричной трактовке) имеет интеграл
| I(ξ, η, C) = 0, |
из которого удается выразить решение уравнения (1), например, в виде
| ξ = ξ(σ), η = η(σ), |
| t = Φ[ξ(σ), η(σ)], x = Ψ[ξ(σ), η(σ)] |
представляет собой параметризацию решения уравнения (1). Разумеется, нужно внимательно следить за эквивалентностью переходов и, в частности, за отличием от нуля соответствующих дифференциалов (см. задачи О6.13 и О6.14).
Задача О6.9. Проинтегрируйте уравнение
| x(x′)2 + 2tx2 – x = 0. |
Литературные указания. Исследование дифференциальных
уравнений, не разрешенных относительно старшей производной,
можно найти почти в каждом учебнике по обыкновенным
дифференциальным уравнениям (см., напр.,
[Айнс,
Арнольд,
Бибиков,
Задачи. О6.10. Пусть в уравнении F(t, x) = 0 функция
F:
О6.11. Пусть f и g — заданные на R непрерывные функции
и
О6.12. Докажите, что через каждую точку графика особого решения проходит бесконечное число интегральных кривых.
О6.13. Пусть ξ =
u(η) — решение уравнения (12) на
промежутке J и
О6.14. Пусть x =
φ(t) — решение уравнения (1)
и пусть прообраз в D при отображении
О6.15. Пусть F — непрерывная функция. Покажите, что
|
О6.16. Пусть в уравнении f(x′) –
t = 0 функция f: R → R
непрерывно дифференцируема. При каких условиях функции
|
О6.17. Для уравнения Лагранжа
| x = tf(x′) + g(x′) |
с непрерывно дифференцируемыми функциями f и g естественной
параметризацией поверхности S является следующая:
| x = tx′ + f(x′) |
называется уравнением Клеро.
Пусть в нем f: R → R
дважды непрерывно дифференцируема и
О6.19. Опишите множество решений уравнения Клеро x = tx′ – (x′)2.
О6.20. Опишите множество решений уравнения Клеро x = tx′ – (x′)3 (обратите внимание, что для него условия задачи О6.18 не выполнены).
File based on translation from
TEX by TTH,
version 2.32.
Created 16 Jan 2000, 16:53.
Last modified 23 Apr 2002.