§ О23. Экспоненциальная дихотомия

Понятие экспоненциальной дихотомии — это дальнейшее развитие вариаций на тему "Характеристические показатели Ляпунова в теории обыкновенных дифференциальных уравнений".

Как обычно, начнем с поясняющих примеров. Рассмотрим линейное скалярное обыкновенное дифференциальное уравнение

x′ – ax = f(t)

(1)

в котором a ∈ R, а f: R → R — непрерывная ограниченная функция. Легко видеть, что уравнение (1) имеет при любой такой f единственное ограниченное на всей оси решение в том и только том случае, если a ≠ 0. Действительно, если a > 0, то функция

x(t) = ∫ t –∞ ea(t–s)f(s) ds

представляет собой ограниченное на всей оси решение уравнения (1) (докажите!). Если же a < 0, то таким решением является функция

x(t) = ∫ t –∞ e–a(t–s)f(s) ds

Единственность полученного решения очевидна.

Задача О23.1. Докажите, что система дифференциальных уравнений

x′1– a1x1 = f1(t),    x′2– a2x2 = f2(t)

(2)

при любой непрерывной ограниченной на всей оси функции f = (f₁, f₂): R → R² имеет единственное ограниченное на всей оси решение x: R → R² в том и только том случае, если a₁ и a₂ отличны от нуля.

С другой стороны, отличие коэффициентов a₁ и a₂ в системе (2) от нуля означает возможность представления любого решения соответствующей однородной системы в виде суммы экспоненциально растущего и экспоненциально убывающего решений (одно из них может быть тривиальным). Например, если a₁ < 0 и a₂ > 0, то любое решение однородной системы представимо в виде

x(t) = (x1(t), x2(t)) = (C1ea1t, 0) + (0, C2ea2t),

причем, первое решение в правой части убывает как экспонента, а второе — растет как экспонента.

Таким образом, для системы уравнений (2) ее однозначная разрешимость в классе ограниченных на всей оси функций при любой ограниченной на всей оси правой части эквивалентна возможности представления любого решения однородной системы в виде суммы экспоненциально растущего и экспоненциально убывающего решений. Обобщение этого факта на более широкий класс уравнений составляет предмет данного очерка, а сама возможность такого представления решений однородного уравнения как раз и называется экспоненциальной дихотомией.

Перейдем к точным формулировкам. Мы будем рассматривать линейную систему обыкновенных дифференциальных уравнений

[Lx](t) ≡ x′(t) – A(t)x(t) = f(t),

(3)

в которой A(t) — n×n-матрица-функция с непрерывными ограниченными на всей оси коэффициентами, а f: R →Rn — непрерывная ограниченная на всей оси функция. Ниже систематически используются два банаховых пространства: C — пространство непрерывных ограниченных на всей оси функций x: R → R с нормой ||x||C = sup{||x(t)||: t ∈ R} и C1 — пространство непрерывно дифференцируемых функций x ∈ C таких, что x′ ∈ C, с нормой ||x||C1 = ||x||C + ||x′||C.

Задача О23.2. Покажите, что определенный равенством (3) дифференциальный оператор L — это линейный ограниченный оператор, действующий из C¹ в C.

Однозначная разрешимость уравнения (3) в C¹ при любой правой части f ∈ C означает, очевидно, обратимость оператора L как оператора из C¹ в C.

Пространство всех решений соответствующего однородного уравнения

x′ = A(t)x

(4)

в соответствии с выводами общей теории линейных уравнений представляет собой линейное n-мерное пространство; обозначим его через X. Говорят, что для уравнения (4) имеет место экспоненциальная дихотомия, если пространство X представимо в виде прямой суммы X₊ ⊕ X_– и при некоторых положительных M₊, γ₊, M_–, γ_– выполнены следующие условия

(+)  если x ∈ X+, то ||x(t)|| ≤ M+e–γ+(t–s)||x(s)|| при всех s ≤ t; (–)  если x ∈ X–, то ||x(t)|| ≥ M–eγ–(t–s)||x(s)|| при всех s ≤ t

(см. рис. 1).

Рис. 1.

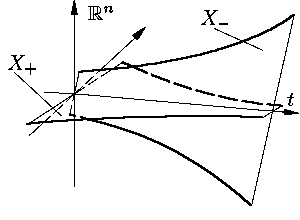
Задача О23.3. Докажите, что κ(x) ≤ –γ₊ при всех x ∈ X₊ и κ(x) ≥ γ_– при x ∈ X_– (здесь κ — генеральный показатель Боля).

Основным утверждение этого раздела теории дифференциальных уравнений является следующая

Теорема об экспоненциальной дихотомии. Оператор L: C¹ → C обратим в том и только том случае, если для уравнения (4) имеет место экспоненциальная дихотомия решений.

Д о к а з а т е л ь с т в о  этого фундаментального утверждения достаточно громоздко, поэтому мы ограничимся существенно более простой ситуацией уравнения с постоянными коэффициентами, попутно получив критерий экспоненциальной дихотомии для таких уравнений, формулируемый в терминах спектра матрицы уравнения. Итак, рассмотрим (для определенности, вещественное) уравнение

x′ = Ax

(5)

с постоянной вещественной n×n-матрицей A и соответствующий ему дифференциальный оператор [Lx](t) ≡ x′(t) – Ax(t). Оказывается, следующие три утверждения эквивалентны:

(а) оператор L: C¹ → C обратим;

(б) матрица A не имеет чисто мнимых собственных значений;

(в) уравнение (5) допускает экспоненциальную дихотомию.

Задача О23.4. Покажите, что (а) ⇒ (б) и (в) ⇒ (б) (предположите противное).

Докажем теперь импликацию (б) ⇒ (в). Пусть e₁, ..., e_n — базис (вещественных) собственных и присоединенных векторов оператора A, причем, первые l отвечают собственным значениям с отрицательной вещественной частью, а остальные — с положительно (по предположению, чисто мнимых собственных значений нет). Обозначим далее через E₊ линейную оболочку векторов e₁, ..., e_l, а через E_– — линейную оболочку векторов e_l+1, ..., e_n. Очевидно, E₊ ⊕ E_– = Rⁿ.

Задача О23.5. Пусть Φ(t) — нормальная в нуле фундаментальная матрица уравнения (5) (т. е. матрица оператора сдвига g^t = e^At). Покажите, что Φ(t)E₊ ⊆ E₊ и Φ(t)E_– ⊆ E_– при всех t ∈ R.

Обозначим через X₊ множество определенных на R решений уравнения (5), значения которых в нулевой момент времени лежат в E₊; X_– определяется по E_– аналогично (см. рис. 2).

Рис. 2.

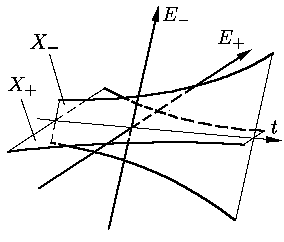
Задача О23.6. Покажите, что X = X₊ ⊕ X_–.

Осталось проверить выполнение условий (+) и (–) в определении дихотомии. Докажем, например, выполнение условия (+). Обозначим через A₊ сужение оператора A на E₊. Тогда (см. курс алгебры) спектр σ(A₊) оператора A₊ состоит из всех точек спектра оператора A с отрицательными вещественными частями. Пусть γ₊ > 0 таково, что Re λ ≤ –γ₊ при всех λ ∈ σ(A₊). Далее, очевидно, если x₊ ∈ X₊, то

x′+(t)≡ A+x+(t).

Положим φ(t) = (x₊(t), x₊(t)) = ||x₊(t)||². Тогда

φ′(t) = (x′+(t), x+(t)) + (x+(t), x′+(t))= = (A+x(t), x+(t)) + (x+(t), Ax+(t)) = ((A+ + A*+)x+(t), x+(t)),

(6)

где A*+— оператор, сопряженный к A+. Как известно из того же курса алгебры, во-первых, оператор H = A+ + A*+ самосопряжен, во-вторых, спектр оператора H получается проектированием спектра оператора A+ на вещественную ось и умножением на два (поэтому, в частности, λ ≤ –2γ+ при λ ∈ σ(H)) и, наконец, в-третьих, поскольку оператор H самосопряжен, (Hx, x) ≤ 2γ+(x, x) при всех x ∈ E+. Поэтому, продолжая (6), получаем

φ′(t) = (Hx+(t), x+(t)) = –2γ+(x+(t), x+(t)) = –2γ+φ(t).

По теореме о нестрогих дифференциальных неравенствах

φ(t) ≤ e–2γ+(t–s)φ(s) при t ≥ s,

или

||x+(t)|| = [φ(t)]1/2 ≤ e–γ+(t–s)[φ(s)]1/2 = e–γ+(t–s)||x+(s)|| при t ≥ s,

что и требовалось.

Задача О23.7. Докажите выполнение условия (–).

Импликация (б) ⇒ (в) доказана. Докажем теперь, что из (б) следует (а). Пусть опять спектр оператора A не содержит чисто мнимых точек. Мы предъявим явную формулу, задающую оператор L^–1. Пусть Φ(t), E₊ и E_– такие же, как и выше, а P₊ и P_– проекторы Rⁿ на E₊ параллельно E_– и на E_– параллельно E₊, соответственно. Положим

G(t, s) = { Φ(t)P+Φ–1(s) при t ≥ s, –Φ(t)P–Φ–1(s) при t <s

(7)

(мы намеренно не используем явный вид Φ(t) как экспоненты оператора tA, имея в виду возможность обобщения на неавтономные уравнения). Покажем, что формула

(Lf)(t) = ∫ ∞ –∞ G(t, s)f(s) ds

(8)

определяет оператор L обратный к L: C¹ → C. Для этого сначала докажем, что L определен на C, для чего, в свою очередь, достаточно доказать, что

||G(t, s)|| ≤ Me–γ|t–s|

(9)

с некоторыми M, γ > 0. Пусть, например, t ≥ s и пусть x ∈ Rⁿ. Обозначим Φ(t)P₊Φ^–1(s)x через x₊(t). Очевидно, x₊ ∈ X₊ и поэтому в силу (+)

||x+(t)|| ≤ M+e–γ+(t–s)||x+(s)|| при t ≥ s,

или

||x+(t)|| ≤ M+e–γ+(t–s)||Φ(t)P+Φ–1(s)x|| при t ≥ s.

(10)

Так как Φ(s) = e^tA коммутирует с проектором P₊ на собственное подпространство E₊ оператора A, Φ(t)P₊Φ^–1(s) = P₊ и, следовательно, ||Φ(t)P₊Φ^–1(s)x|| ≤ ||P₊||·||x|| ≡ M||x||. Поэтому (10) можно переписать в виде

||G(t, s)x|| = ||x+(t)|| ≤ Me–γ+(t–s)||x||

и неравенство (9) при t ≥ s доказано. Доказательство (9) при t ≤ s аналогично.

Покажем, что функция x = Lf является решением уравнения Lx = f, предоставляя читателю возможность самому обосновать правомерность проводимых ниже действий. Итак,

x′(t) = d dt ( ∫ t –∞ G(t, s)f(s) ds ) + d dt ( ∫ ∞ t G(t, s)f(s) ds ) =

= ∫ t –∞ ∂ ∂t G′t(t,s)f(s) ds + G(t, t – 0)f(t) +

(11)

+ ∫ ∞ t ∂ ∂t G′t(t,s)f(s) ds + G(t, t + 0)f(t).

Заметим теперь, что, во-первых,

d dt G(t, s) =  { Φ′(t)P+Φ–1(s) при t ≥ s, –Φ′(t)P–Φ–1(s) при t < s =

=  { AΦ(t)P+Φ–1(s) при t ≥ s, –AΦ(t)P–Φ–1(s) при t < s = AG(t, s)

и, во-вторых,

G(t, t – 0)f(t) – G(t, t + 0)f(t) = [Φ(t)P+Φ–1(t) + + Φ(t)P–Φ–1(t)]f(t) = Φ(t)(P+ + P–)Φ–1(t)f(t) = f(t).

Поэтому, продолжая (11), получаем

x′(t) = ∫ t –∞ AG(t, s)f(s) ds + ∫ ∞ t AG(t, s)f(s) ds + f(t) =

= A ∫ ∞ –∞ G(t, s)f(s) ds + f(t) = Ax(t) + f(t),

то есть Lx = f, что и требовалось доказать.

Матрица-функция G(t, s), являющаяся ядром интегрального представления оператора L^–1, называется функцией Грина оператора L. Она играет важную роль в теории дифференциальных уравнений. Например, информация о ее свойствах позволяет исследовать нелинейный интегральный оператор

(Fx)(t) = ∫ ∞ –∞ G(t, s)f[s, x(s)] ds,

возникающий в задаче об ограниченных на всей оси решениях нелинейного уравнения

x′ – A(t)x = f(t, x).

Литературные указания. Вопросы, связанные с дихотомией решений дифференциальных уравнений в учебниках обычно не описываются или приводятся в простейшей ситуации уравнений с постоянными коэффициентами. Поэтому мы отсылаем читателя к монографической литературе [Красносельский — Бурд — Колесов, Левитан — Жиков, Хартман, Coppell]. В [Далецкий — Крейн, Массера — Шеффер] можно найти систематическое изложение этих вопросов для дифференциальных уравнений в банаховых пространствах.

Задачи. О23.8. Пусть для уравнения (4) имеет место экспоненциальная дихотомия и X_– = {0}. Докажите, что уравнение (4) экспоненциально устойчиво.

О23.9. Докажите, что если уравнение (4) равномерно асимптотически устойчиво, то для него имеет место экспоненциальная дихотомия.

О23.10. Докажите, что для уравнения (4) и для уравнения x′ + A(–t)x = 0 экспоненциальная дихотомия имеет место одновременно. Как связаны соответствующие подпространства X₊ и X_– для этих уравнений?

О23.11. Докажите, что если для уравнения (4) имеет место экспоненциальная дихотомия, то имеет место экспоненциальная дихотомия и для уравнения x′ – A*(t)x = 0.

О23.12. Докажите, что заменой x = e^λty при некотором λ ∈ R любое уравнение вида (5) преобразовывается к уравнению, имеющему экспоненциальную дихотомию.

О23.13. Пусть в скалярном уравнении x′ – a(t)x = 0 коэффициент a является непрерывной T-периодической функцией. Покажите, что для этого уравнения имеет место экспоненциальная дихотомия в том и только том случае, если ∫0Ta(s) ds ≠ 0.

О23.14. Докажите, что если в уравнении (4) матрица A(t) периодическая, то для экспоненциальной дихотомии необходимо и достаточно, чтобы это уравнение не имело ненулевых ограниченных на всей оси решений.

О23.15. Пусть A(t) и B(t) — непрерывные ограниченные на всей оси n×n-матрицы-функции. Докажите, что если для уравнения (4) имеет место экспоненциальная дихотомия, то при достаточно малых ε имеет место экспоненциальная дихотомия и для уравнения x′ – A(t)x – εB(t)x = 0.

О23.16. Пусть для уравнения (5) имеет место экспоненциальная дихотомия, а B — постоянная n×n-матрица. Пусть P+ε и P–ε — соответствующие проекторы, отвечающие уравнению x′ – Ax – εBx = 0 (ε малó; см. предыдущую задачу). Покажите, что ||P+ε – P+0|| → 0 и ||P–ε – P–0|| → 0 при ε → 0.

О23.17. Докажите единственность разложения X = X₊ ⊕ X_–, удовлетворяющего условиям (+) и (–).

О23.18. Пусть для уравнения (4) имеет место экспоненциальная дихотомия. Положим E_± = {x(0): x ∈ X_±} и пусть P₊ и P_– — проекторы в Rⁿ на E₊ и E_– параллельно E_– и E₊, соответственно. Пусть, наконец, Φ(t) — нормальная в нуле фундаментальная матрица уравнения (4), а P_±(t) = Φ(t)P_±Φ^–1(t). Докажите, что ||P₊(t)|| и ||P_–(t)|| ограничены на всей оси.

О23.19. В условиях предыдущей задачи докажите, что E₊ (соответственно, E_–) в точности совпадает со множеством начальных значений (при t = 0) ограниченных вправо (соответственно, влево) решений.

О23.20. Используя результаты задачи О23.10, докажите, что задаваемая формулой (7) функция Грина оператора (Lx)(t) = x′ – A(t)x удовлетворяет оценке (9).

О23.21. Докажите, что если для уравнения (4) имеет место экспоненциальная дихотомия, то формула (8) задает оператор, обратный к оператору L: C¹ → C.

File based on translation from T_EX by T_TH, version 2.32.
Created 26 Feb 2000, 20:11.
Last modified 29 Apr 2002.