§ О19. Вынужденные колебания линейных систем

Колебательные движения (в интуитивном понимании этого термина) являются едва ли не самым распространенным типом движений в природе. Среди всего многообразия колебаний можно выделить два больших класса. Это, во-первых, автоколебания, источником которых служат внутренние свойства системы. Таковыми являются, например, колебания, описываемые предельными циклами динамических систем. И, во-вторых, так называемые вынужденные колебания, существующие как результат внешнего воздействия колебательной природы. Эта классификация, разумеется, в некоторой мере условна. Так, например, приливные колебания, вызванные Луной, могут рассматриваться и как автоколебательные, если они описываются в изолированной системе Земля — Луна, и как вынужденные, если рассматривать Землю как замкнутую систему, подвергаемую внешнему воздействию гравитационного поля Луны.

Здесь мы рассмотрим вынужденные колебания, описываемые линейными дифференциальными уравнениями. Основной источник таких задач — это линеаризация нелинейных дифференциальных уравнений в окрестности положения равновесия. Все характерные явления мы покажем на примере линейного (гармонического) осциллятора с одной степенью свободы. Рассмотрим сначала случай осциллятора без трения. Если на него не действуют никакие внешние силы, то он описывается уравнением

\

x′′ + ω2x = 0.

(1)

Матрица соответствующей линейной системы

x′1= x2,    x′2= –ω2x1

очевидно имеет чисто мнимые собственные значения ±iω, поэтому общее (вещественное) решение уравнения (1) имеет вид

x(t) = C1cos ωt + C2sin ωt,

где C₁, C₂ — произвольные вещественные постоянные. После элементарных преобразований это решение может быть представлено в следующем виде

x(t) = a·cos(ωt + φ).

(2)

Описываемые этой формулой колебания называются свободными или собственными колебаниями системы, число a при этом называется амплитудой, а φ — фазой свободных колебаний. За счет выбора амплитуды и фазы можно удовлетворить произвольные начальные условия для уравнения (1).

Предположим теперь, что на наш осциллятор действует периодическая сила f и, более того, пока будем считать, что эта сила гармоническая: f(t) = r · cos νt. Движения осциллятора тогда описывается уравнением

x′′ + ω2x = r · cos νt.

(3)

В соответствии с теорией линейных дифференциальных уравнений общее решение уравнения (3) представляет собой сумму общего решения (2) однородного уравнения (1) и частного решения неоднородного уравнения (3). Последнее можно найти методом неопределенных коэффициентов в виде x_чн(t) = C · cos(νt + θ), если ν ≠ ω и в виде x_чн(t) = Ct · cos(νt + θ), если ν = ω.

Задача О19.1. Докажите, что если ν ≠ ω, то x_чн(t) = [r/(ω² – ν²)]cos νt, а если ν = ω, то x_чн(t) = [r/2ω]t·sin νt.

Таким образом, общее решение уравнения (3) имеет вид

x(t) = a · cos(ωt + φ) + r ω2 – ν2 cos νt,

(4)

если ν ≠ ω, и

x(t) = a · cos(ωt + φ) + r 2ω cos νt,

если ν = ω (a и φ — произвольные постоянные; их выбором можно удовлетворить любые начальные условия для уравнения (3)). Первое слагаемое в правых частях этих формул представляет свободные колебания осциллятора; их частота ω определяется внутренними свойствами системы, а амплитуда a и фаза φ — начальными условиями и внешними воздействиями. Второе слагаемое, называемое вынужденными колебаниями, обусловлено наличием внешней (вынуждающей) силы. Их частота полностью определяется частотой внешней силы, а амплитуда — соотношением собственной и вынуждающей частот ω и ν и амплитудой вынуждающей силы r.

Если частота ν вынуждающей силы стремится к частоте ω собственных колебаний осциллятора, то амплитуда r/|ω² – ν²|, очевидно, неограниченно возрастает (см. рис. 1). Это явление называется резонансом. При резонансном значении ν = ω вынуждающей силы результирующие колебания растут неограниченно — их амплитуда растет как линейная функция времени. Таким образом, если частота вынуждающей силы близка к резонансной частоте, то даже очень малой внешней силой можно вызвать ощутимые колебания в системе.

Рис. 1.

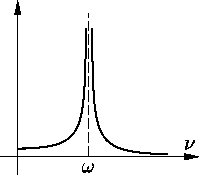
Явление резонанса играет важную роль в приложениях. Так, деку скрипки стараются сделать таким образом, чтобы она хорошо резонировала (т. е. усиливала звуки) на большом спектре частот. В то же время, конструкции зданий, мостов, плотин, двигателей, механических передач и т. д. подбирают так, чтобы собственные их частоты лежали далеко от частот характерных внешних воздействий. В противном случае возможно разрушение.

Легко видеть, что вынужденные колебания линейного осциллятора, вызванные внешней силой очень большой частоты, имеют малую амплитуду (см. рис. 1). Это свойство колебательных систем называется фильтром высоких частот (осциллятор почти "не пропускает" высокочастотные возмущения).

В общем случае колебания, задаваемые формулой (4), представляют собой почти периодические функции и периодическими не являются (они будут таковыми только если ν и ω соизмеримы, т. е. ν/ω рационально (докажите!)). При приближении ν к ω они имеют специфическую форму. Пусть, для простоты, начальные условия нулевые. Тогда, как легко видеть,

x(t) = r ω2 – ν2 [cosνt – cos ωt] = 2r ω2 – ν2 sin ( ω – ν 2 t ) sin ( ω – ν 2 t ) .

Эти колебания можно рассматривать как периодические частоты (ω + ν)/2 ≈ ω с медленно меняющейся амплитудой [2r/(ω² – ν²)] · sin[(ω – ν)t/2] (см. рис. 2). Такие колебания называются биениями. При ν → ω период биений неограниченно растет и при резонансном значении частоты вынуждающей силы становится бесконечным (см. рис. 3).

Рис. 2.

Рис. 3.

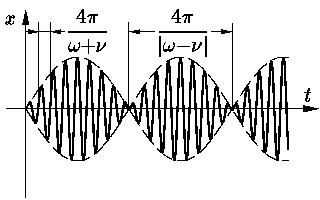
Задача О19.2. Покажите,что при произвольных начальных условиях вынужденные колебания (3) представимы в виде

x(t) = r ω2 – ν2 Φ(t) + Ψ(t),

где Φ(t) представляют собой биения, а амплитуда Ψ(t) мала по сравнению с r/(ω² – ν²) при ν близких к ω.

На практике неограниченного возрастания амплитуды колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний не наблюдается в основном по двум причинам. Во-первых, при больших амплитудах линейные уравнения, как правило, перестают адекватно описывать реальную систему — начинают сказываться нелинейные эффекты (например, при описании колебаний грузика на пружине перестает действовать линейный закон Гука, утверждающий пропорциональность силы реакции пружины степени ее растяжения). Во-вторых, рассмотренное уравнение линейного осциллятора не учитывает силы трения, всегда реально присутствующей. Выяснением роли трения мы сейчас займемся.

Уравнение, описывающее свободные колебания линейного осциллятора с трением имеет вид

x′′ + cx′ + ω2x = 0   (c > 0).

(5)

Характеристические числа этого уравнения, очевидно, равны λ_1,2 = –γ_c ± iω_c, где γ_c = c/2, а ω_c = (4ω² – c²)^1/2 (и следовательно, всегда имеют отрицательную вещественную часть).

Задача О19.3. Покажите,что если коэффициент трения достаточно мал, а именно, c < 2ω, то общее решение уравнения (5) имеет вид x(t) = a·e – γc tcos(ωct + φ).

Пусть теперь на осциллятор с трением действует вынуждающая сила (мы опять пока предполагаем, что она гармоническая):

x′′ + cx′ + ω2x = r·cos νt.

(6)

Задача О19.4. Докажите,что уравнение (6) имеет решение вида x(t) = A·cos(νt + ψ), в котором A = r/[(ω² – ν²)² + c²ν²]^1/2.

Итак, общее решение уравнения (6) имеет вид

x(t) = a·e–γc tcos(ωt + φ) + r √ (ω2 – ν2)2 + c2ν2 cos(νt + ψ).

Как и в случае осциллятора без трения, колебания осциллятора с трением состоят из свободных колебаний a·e–γctcos(ωt + φ), определяемых внутренними свойствами системы, и вынужденных колебаний, определяемых внешней силой. Но в отличие от осциллятора без трения, во-первых, свободные колебания затухают с экспоненциальной скоростью и, в конце концов, система совершает только вынужденные колебания. И, во-вторых, амплитуда вынужденных колебаний при приближении частоты ν вынуждающей силы к частоте ω не возрастает неограниченно, а лишь до некоторой конечной величины (см. рис. 4, на котором сплошной линией изображена зависимость от ν амплитуды вынужденных колебаний осциллятора с трением, а пунктирной — без трения).

Рис. 4.

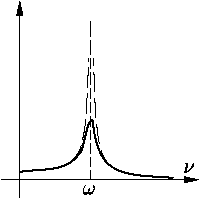
Задача О19.5. Исследуйте эту зависимость для осциллятора с трением. В частности, найдите максимальное значение амплитуды и значение ν, при котором оно достигается.

Задача О19.6. Исследуйте зависимость амплитуды вынужденных колебаний и собственные частоты осциллятора mx′′ + cx′ + lx = 0 от его массы m, коэффициента трения c и жесткости пружины l.

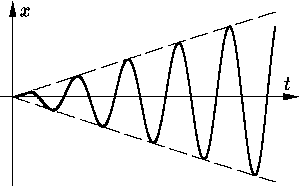
Колебания осциллятора при наличии малого трения при частоте вынуждающей силы, близкой к частоте собственных колебаний, начинаются с биений, но с течением времени в них остаются только вынужденные колебания (см. рис. 5).

Рис. 5.

Задача О19.7. Аналитически обоснуйте последнее утверждение.

Поясним в заключение, как можно действовать, если вынуждающая сила не является гармонической. Пусть, например, на осциллятор без трения действует 2π/ν-периодическая вынуждающая сила f и предположим, что f представима в виде суммы сходящегося ряда Фурье

f(t) = ∞ ∑ k = 0 rkek(t),

(7)

где e₀(t) ≡ 1, e_2k–1(t) = sin kνt, e_2k(t) = cos kνt (последнее предположение выполняется практически во всех важных в приложениях случаях; проверяемые признаки его выполнения можно найти в любом курсе математического анализа). В соответствии с общей теорией линейных уравнений решение уравнения

x′′ + ω2x = f(t)

представимо в виде формального ряда

x(t) = a·cos(νt + φ) + ∞ ∑ k = 0 xk(t),

где x_k(t) — вынужденные колебания этого осциллятора с вынуждающей силой r_ke_k(t). Компоненты x_k(t) находятся описанным выше способом. Если при каком-либо k выполняется равенство kν = ω, то имеет место резонанс с k-ой гармоникой (или резонанс k-го рода ) и тогда x_k следует находить как в резонансном случае. Сходимость ряда исследуется обычными методами. Аналогично поступают и в случае осциллятора с трением. На практике обычно ограничиваются конечным отрезком ряда Фурье. Подчеркнем, что важную роль играет близость частоты той или иной гармоники к резонансной частоте системы, даже если она входит в ряд (7) с малым коэффициентом.

Литературные указания. Результаты данного очерка элементарны и могут быть найдены во многих учебниках и монографиях (см., напр., [Андронов — Витт — Хайкин, Арнольд, Бутенин, Карташов — Рождественский, Стокер, Цзе — Морзе — Хинкл].

Задачи. О19.8. Исследуйте случай вынужденных колебаний линейного осциллятора с трением при c ≥ 2ω.

О19.9. Исследуйте случай вынужденных колебаний линейного осциллятора с отрицательным трением: r < 0.

О19.10. Являются ли вынужденные колебания осцилляторов с трением и без трения устойчивыми? Асимптотически устойчивыми?

О19.11. Найдите вынужденные колебания систем x′′ + ω²x = 1 и x′′ + cx′ + ω²x = 1 (c > 0). Исследуйте их устойчивость.

О19.12. Метод комплексной амплитуды нахождения вынужденных колебаний осциллятора x′′ + cx′ + ω²x = f(t) ≡ r · cos νt заключается в представлении f(t) в виде Re F(t), где F(t) = r · e^iνt, последующем нахождении решения уравнения в виде C · e^iνt (или, если c = 0 и ν = ω, в виде Ct · e^iνt), где C — комплексное число. Вынужденные колебания тогда задаются формулой x_чн(t) = Re C · e^iνt. Если C = a · e^iφ, то a является амплитудой, а φ — фазой вынужденных колебаний (C называется комплексной амплитудой). Обоснуйте метод комплексной амплитуды.

О19.13. Исследуйте зависимость фазы вынужденных колебаний осциллятора с трением от частоты вынуждающей силы.

О19.14. Как изменяется по времени энергия E = ¹/₂(x′)² + ¹/₂x² свободных и вынужденных колебаний линейного осциллятора без трения? Что происходит с энергией при резонансе?

О19.15. Исследуйте зависимость полной энергии свободных и вынужденных колебаний линейного осциллятора с трением от времени, от частоты вынуждающей силы.

О19.16. Перенесите результаты очерка на системы обыкновенных дифференциальных уравнений в Rⁿ вида

x′′ + ω2x = 0,

(8)

где ω² = diag(ω²₁, ..., ω²_n) — диагональная n×n-матрица.

О19.17. Пусть A и B — две положительные n×n-матрицы, T(x) = ¹/₂(Ax, x), U(x) = ¹/₂(Bx, x). Из курса теоретической механики известно, что систему уравнений Лагранжа, описывающую малые колебания консервативной системы с n степенями свободы,

d dt ∂T(x′) ∂x′ = ∂T(x) ∂x – ∂U(x) ∂x

(9)

заменой переменных x = Cy можно привести к виду (8). Перенесите результаты очерка на системы вида (9).

О19.18. Как могут выглядеть результаты очерка в применении к уравнению

x(n) + an–1x(n–1) + ... + a1x′ + a0x = 0?

Какое условие может играть роль наличия трения?

О19.19. Полная энергия консервативной системы (9), по определению, есть E = T(x) + U(x). Как изменяется полная энергия вынужденных колебаний этой системы со временем?

О19.20. Исследуйте зависимость амплитуды вынужденных колебаний системы двух осцилляторов

x′′1+ ω21x1= r · sin νt,    x′′2+ ω22x2= 0

от частоты вынуждающей силы ν.

О19.21. Аналогичный вопрос для осцилляторов с малым трением

x′′1+ c1x′1+ ω21x1= r · sin νt,    x′′2+ c2x′2+ ω22x2= 0.

О19.22. Аналогичный вопрос для осцилляторов

x′′1+ ω21x1= r1 · sin νt,    x′′2+ ω22x2= r2 · sinνt.

и соответствующих осцилляторов с трением.

О19.23. Наконец, исследуйте зависимость амплитуды вынужденных колебаний осциллятора

x′′1+ ω21x1= r1 · sin ν1t,    x′′2+ ω22x2= r2 · sin ν2t.

от частот ν₁ и ν₂.

File based on translation from T_EX by T_TH, version 2.32.
Created 24 Feb 2000, 07:07.
Last modified 28 Apr 2002.