
|
§ 3.4. Метод неопределенных коэффициентов для линейных автономных систем |

|
... меня заинтересовали практические выводы из моих теоретических работ.
Ф. Дюрренматт. Физики
Полученное в предыдущем параграфе
представление eAt
требует вычисления жордановой нормальной
формы J матрицы A и
приводящей матрицы P,
что является достаточно сложной задачей. Практически бывает
удобнее находить фундаментальную матрицу
eAtP = PeJt.
В данном параграфе мы подробно опишем вид столбцов этой
матрицы, и это позволит находить их методом неопределенных
коэффициентов.
3.4.1. Утверждение о решениях вида
eλtq.
Функция eλtq
(λ ∈
C, q ∈
Kn)
является ненулевым решением системы
тогда и только тогда, когда λ
есть собственное значение матрицы A,
а q — соответствующий собственный вектор.
Если матрица A имеет n линейно независимых собственных векторов qk
с (не обязательно различными) собственными значениями
λk, то функции
|
φk(t) =
eλk tqk
(k = 1, 2, ..., n)
| (1) |
образуют фундаментальную систему решений
(ЛАОС).
Д о к а з а т е л ь с т в о. Если
eλtq — ненулевое решение
(ЛАОС), то
т. е.
Следовательно, λ —
собственное значение A
и q — соответствующий собственный вектор. Наоборот,
из (3) умножением на
eλt
получаем (2), т. е.
eλtq
удовлетворяет (ЛАОС).
Система решений вида (1) с линейно
независимыми qk,
очевидно, фундаментальна, так как при
значения этих решений линейно независимы.
В частности, если все n собственных
значений λk
матрицы A различны, то соответствующие собственные
векторы qk
линейно независимы, т. е. система (1) фундаментальна.
3.4.2. Пример. Найдем фундаментальную
систему решений вида (1) для системы
(ω ≠ 0). Сначала ищем
собственные значения
λk матрицы
и убеждаемся, что они различны:
|
(A – λI) = 0 ⇔ λ2 +
ω2 = 0 ⇔ λ1, 2 =
±iω. |
Итак, в данном случае фундаментальная система
решений (1) имеет вид:
φ1(t) =
eiωt
|
( |
|
) |
, φ2(t) =
e–iωt
|
( |
|
) |
. |
|
Подставим φ1 в (4) и
найдем a и b:
| iωeiωt |
( |
|
) |
= eiωt |
( |
|
) |
( |
|
) |
, |
|
|
iωa = bω,
iωb = –aω ⇐ a = 1,
b = i. |
Нас интересует не вся совокупность решений этой алгебраической линейной однородной системы,
а только ее фундаментальная система решений, которая в данном случае
состоит из одного решения. Таким образом,
Аналогично находим φ2:
|
dω, – iωd =
– cω ⇐ c = 1,
d = – i — |
и, следовательно,
3.4.3. Утверждение о
фундаментальной системе решений (ЛАОС) в общем случае.
(ЛАОС) имеет фундаментальную
систему решений вида
|
φkl(t) =
eλk
tQkl(t),
| (5) |
где
k = 1, 2, ..., p,
l = 1, 2, ..., rk,
λk —
собственное значение
матрицы A алгебраической
кратности rk,
Qkl(t) — многочлен от переменной t с векторными
коэффициентами, причем его степень
deg(Qkl) ≤
maxs{r(k, s)} – 1
≤ rk – 1.
Д о к а з а т е л ь с т в о. Как отмечено выше, (ЛАОС)
имеет фундаментальную матрицу
где eJt —
блочно-диагональная матрица с блоками вида
(11) из
п. 3.3.5.
Заметим, что в соответствии с (6) столбцы матрицы
Φ(t) получаются умножением
матрицы P на соответствующие столбцы eJt.
Будем нумеровать столбцы eJt и
Φ(t)
двумя индексами: k = 1, 2, ...,
p — номер блока, в который входит этот столбец в
eJt, и l =
1, 2, ..., rk —
номер столбца в этом блоке. Тогда из формулы (11)
п.3.3.5 следует, что
где столбец ψkl(t)
состоит из нулей и функций вида tm/m!,
m ≤
maxs{r(k,
s)} – 1 ≤
rk – 1. Положив
Qkl =
Pψkl,
получаем (5).
3.4.4. Определение квазимногочлена.
Квазимногочленом называется функция вида
| φ(t) = |
p
∑
k = 1
|
eλk tQk(t),
|
| (7) |
где Qk(t) — многочлены от t,
а λk
∈ C — показатели
квазимногочлена. Если многочлены Qk
имеют векторные коэффициенты, то квазимногочлен называется
векторным.
П р и м е р. Любое решение (ЛАОС) есть векторный
квазимногочлен, показатели которого — собственные значения матрицы A.
Это следует из п. 3.4.3 и того факта,
что любое решение есть линейная комбинация
фундаментальной системы решений.
3.4.5. Лемма о квазимногочлене.
Пусть показатели λk
квазимногочлена (7) различны.
Утверждается, что если
то
|
Qk(t) ≡ 0
(k = 1, 2, ..., p). |
Д о к а з а т е л ь с т в о проводится индукцией по p.
Для p = 1 утверждение очевидно. Пусть оно справедливо для некоторого p, и пусть
p + 1
∑
k = 1
|
eλk
tQk(t) =
eλ1
tQ1(t) +
|
p + 1
∑
k = 2
|
eλk
tQk(t) ≡
0.
|
|
Тогда
| Q1(t) + |
p + 1
∑
k = 2
|
e(λk–λ1)tQk(t)
≡ 0.
|
| (8) |
Полученное тождество будем последовательно дифференцировать по t
до тех пор, пока первое слагаемое не обратится в нуль. Заметим, что
d
dt
|
[eλtQ(t)] =
eλt[λQ(t) +
Q′(t)] =
eλtQ(t).
|
|
Отсюда, в частности, следует, что старший коэффициент
Q получается из старшего
коэффициента Q умножением на λ.
Поэтому, если λ ≠ 0 и
Q(t) 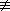 0, то и
0, то и
Путем последовательного дифференцирования мы получим из (8):
p + 1
∑
k = 2
|
e(λk–λ1)tQk(t)
≡0.
|
|
По предположению индукции,
|
Qk(t) ≡ 0
(k = 2, ..., p + 1). |
Учитывая, что λk –
λ1 ≠ 0,
получаем в силу сделанного выше замечания:
|
Qk(t) ≡ 0
(k = 2, ..., p + 1). |
Вместе с (8) это дает:
Q1(t) ≡ 0.
3.4.6. Утверждение о линейной независимости.
Если в произвольной системе решений вида (5) свободные
члены полиномов Qkl при любом фиксированном k
линейно независимы, то вся система (5) линейно независима.
Д о к а з а т е л ь с т в о. Пусть
p
∑
k = 1
|
rk
∑
l = 1
|
ckleλk
tQkl(t) ≡ 0,
|
|
|
т. е.
p
∑
k = 1
|
eλk
tQk(t) ≡ 0,
Qk(t) =
|
rk
∑
l = 1
|
cklQkl(t).
|
|
По лемме о квазимногочлене тогда
rk
∑
l = 1
|
cklQkl(t)
≡ 0 (k = 1, 2,
..., p).
|
|
Поскольку при t = 0 и фиксированном k многочлены
Qkl(t) линейно независимы, отсюда получаем:
|
ckl = 0 (k = 1, 2,
..., p; l = 1, 2, ..., rk). |
Итак, если каким-нибудь способом найти систему решений вида (5),
линейно независимую при любом фиксированном k и t = 0,
то это будет фундаментальная система решений.
Найденная фундаментальная система решений может быть комплексной даже в том случае, когда
матрица A вещественна, так как собственные значения вещественной матрицы
могут быть комплексными. В этом случае возникает задача: преобразовать
комплексную фундаментальную систему решений для (ЛАОС)
с вещественной матрицей A в вещественную фундаментальную систему решений.
3.4.7. Утверждение о вещественной фундаментальной системе
решений. Пусть для (ЛАОС) с вещественной
матрицей A построена комплексная фундаментальная
система решений вида
|
φ1, ...,
φn1;
ψ1, ...,
ψn2;
ψ1, ...,
ψn2
| (9) |
|
где φ1, ...,
φn1 —
вещественные, ψ1, ...,
ψn2 —
комплексные, а ψ1, ...,
ψn2 —
соответствующие комплексно сопряженные.
|
Утверждается, что тогда набор
|
φ1, ...,
φn1;
u1, ..., un2;
v1, ..., vn2;
| (10) |
где
|
uk =
Re ψk,
vk =
Im ψk
(k = 1, 2, ..., n2),
|
есть вещественная фундаментальная система
решений (ЛАОС).
Д о к а з а т е л ь с т в о. Функции (10)
являются решениями (ЛАОС), так как
| uk = |
ψk +
ψk
2 |
, vk = |
ψk –
ψk
2i |
, |
| (11) |
а линейная комбинация решений (ЛАОС) есть решение.
Количество функций в наборе (10) такое же, как и в
(5), т. е. n. Проверим линейную независимость. Пусть
n1
∑
k = 1
|
ckφk + |
n2
∑
j = 1
|
djuj + |
n2
∑
j = 1
|
ejvj = 0. |
|
Отсюда и из (11) получаем:
n1
∑
k = 1
|
ckφk + |
n2
∑
j = 1
| 1
2
|
[ | ( |
dj + | 1
i
|
ej | ) |
ψj + |
( | dj – |
1
i
| ej |
) |
ψj
|
] | = 0. |
|
Ввиду линейной независимости системы (9)
|
ck = 0 (k = 1, 2,
..., n1), |
| dj ± |
1
2
| ej = 0
(j = 1, 2, ..., n2), |
|
т. е.
|
dj = ej = 0
(j = 1, 2, ..., n2). |
П р и м е р. Для системы (4) в
п. 3.4.2 мы нашли
комплексную фундаментальную систему решений
φ1(t) =
eiωt
|
( |
|
) | = |
( |
|
) |
+ i |
( |
|
) |
= ψ1(t), |
|
φ2(t) =
e–iωt
|
( |
|
) |
= |
( |
|
) |
– i |
( |
|
) |
= ψ1(t),
|
|
Поэтому следующая пара образует вещественную фундаментальную
систему решений:
| u1(t) = Re ψ1(t) = |
( |
|
) |
, v1(t) =
Im ψ1(t) = |
( |
|
) |
. |
|
Эту фундаментальную систему решений
мы нашли в п. 3.2.2 другим способом
(подбором).
3.4.8. Утверждение о представлении решений
(ЛАОС) в виде квазимногочленов.
Любое решение φ (ЛАОС)
единственным образом с точностью до порядка слагаемых представляется в виде
векторного квазимногочлена
| φ(t) = |
p
∑
k = 1
|
eλk tQk(t),
|
|
в котором показателями
λk
являются собственные значения матрицы A, а степени многочленов Qk
не превосходят rk – 1,
где rk — алгебраическая
кратность λk.
Д о к а з а т е л ь с т в о. Как уже отмечалось в
п. 3.4.4, возможность представления любого решения в
указанном виде вытекает из утверждения о фундаментальной системе
решений соответствующего вида. Единственность представления
следует из леммы о квазимногочлене: если имеется еще одно
представление
| φ(t) = |
p
∑
k = 1
|
eλk t
|
~
Q
|
k(t), |
|
то
p
∑
k = 1
|
eλk t[Qk(t) –
|
~
Q
|
k(t)] ≡ 0, |
|
так что
3.4.9. Контрольные вопросы
3.4.9.1. Найдите фундаментальную матрицу
системы
3.4.9.2. Найдите общее решение систем
d
dt
|
( |
|
) | = |
( |
| ) |
( |
|
) |
и |
d
dt
|
( |
|
) | = |
( |
| ) |
( |
|
) | . |
|
3.4.9.3. По заданным решениям (ЛАОС)
найдите собственные значения и
собственные векторы матрицы A.
|
3.4.9.5. Почему систему
x′1=
x2,
x′2= –x1
заменой вида y = Tx нельзя свести к системе
y′1=
y1,
y′2=
2y2? |
3.4.10. Задачи
3.4.10.1. Покажите, что если у (ЛАОС) есть
ненулевое ограниченное на всей оси решение, то у матрицы A
есть по крайней мере одно собственное значение
с нулевой вещественной частью.
3.4.10.2. Найдите все начальные значения
x0, для которых решение задачи
Коши
является периодическим.
3.4.10.3.
Найдите eAt для A =
| ( |
| 1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
| ) |
. |
3.4.10.4. Пусть все собственные
значения матрицы A имеют (алгебраические)
кратности, не превосходящие двух. Докажите, что многочлен Q(t)
с векторными коэффициентами большей единицы степени не может быть решением
(ЛАОС).




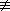 0,
0,