§ О20. Теория осцилляций

Теория осцилляций занимается теми свойствами решений уравнения

y′′ + a1(t)y′ + a0(t)y = 0

(1)

и его обобщений, которые можно охарактеризовать словом "колеблемость". Точнее, основной вопрос теории формулируется так: как часто у нетривиальных решений уравнения (1) встречаются нули? Эта теория находит важные как математические, так и естественнонаучные приложения (см., в частности, очерк О25).

В дальнейшем мы будем предполагать, что a₀ и a₁ — непрерывные на всей оси скалярные функции. Слово "решение" всюду ниже будет обозначать лишь нетривиальные решения уравнения (1).

Первое утверждение в этом направлении, а именно, тот факт, что любое решение уравнения (1) на любом конечном интервале имеет конечное число нулей, доказывается совсем легко. Действительно, если на каком-либо конечном промежутке J некоторое решение φ имеет бесконечное число нулей, скажем t₁, t₂, ..., то в силу компактности промежутка J можно считать, что t_k → t₀ ∈ J при k → ∞. Из равенств φ(t_k) = 0 (k = 1, 2, ...), как легко видеть, следуют равенства

φ(t0) = 0,    φ′(t0) = 0

(докажите!). А так как решение любой задачи Коши для уравнения (1) единственно, последние равенства гарантируют тривиальность решения φ. Противоречие.

Таким образом, решение уравнения (1) может иметь бесконечное число нулей только на бесконечном промежутке. В этом случае оно называется осциллирующим, а в противном случае — неосциллирующим.

Фундаментальная роль в теории осцилляций принадлежит формулируемой и доказываемой ниже теореме Штурма. Она позволяет делать заключение об осцилляционных свойствах решения уравнения (1), сравнивая это уравнение с уравнениями, осцилляционные свойства которых известны.

Прежде чем переходить к формулировке теоремы Штурма сделаем некоторые упрощающие предположения и преобразования. Пусть в уравнении (1) коэффициент a₁ непрерывно дифференцируем.

Задача О20.1. Докажите, что после замены переменных

y = xexp ( – 1 2 ∫ a1(t) dt )

y = x · exp(–1/2 ∫a1(t) dt)

уравнение (1) преобразуется к виду

x′′ + b1(t)x = 0,

(2)

в котором b1(t) = a′1(t)/2– a21(t)/2+ a2(t).

Задача О20.2. Докажите, что решение ψ уравнения (2) является осциллирующим в том и только том случае, если решение φ(t) = ψ(t) · exp(–¹/₂ ∫ a₁(t) dt) уравнения (1) является осциллирующим.

Поэтому мы можем считать задачи об осцилляционных свойствах уравнений (1) и (2) эквивалентными. Наряду с уравнением (2) рассмотрим еще одно уравнение такого же вида

x′′ + b2(t)x = 0,

(3)

с непрерывным коэффициентом b₂.

Теорема Штурма. Пусть b₁(t) ≤ b₂(t) при всех t и пусть t₁, t₂ — последовательные нули решения φ уравнения (2). Тогда любое решение ψ уравнения (3) имеет на промежутке [t₁, t₂] хотя бы один нуль (см. рис. 1).

Рис. 1.

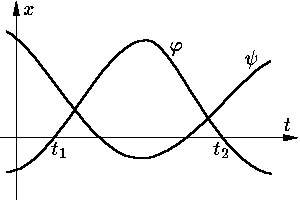
Смысл этой теоремы, если перейти к рассмотрению уравнения малых колебаний маятника (т. е. уравнения гармонических колебаний)

x′′ + ω2x = 0

можно выразить словами: частота колебаний более короткого маятника выше. Простейшие возможности теоремы Штурма демонстрируют следующие две задачи.

Задача О20.3. Сравнивая уравнение (2) с самим собой, докажите, что между последовательными нулями любого решения φ имеется в точности один нуль любого линейно независимого с φ решения. Поэтому нули любых двух решений уравнения (2) либо совпадают, либо чередуются.

Задача О20.4. Сравнивая уравнение (2) с уравнением y′′ = 0, докажите, что если b₁(t) ≤ 0 при всех t, то любое решение уравнения (2) имеет не более одного нуля.

Д о к а з а т е л ь с т в о теоремы Штурма. Предположим противное: решение ψ не имеет нулей на промежутке [t₁, t₂]. Не ограничивая общности, можно считать, что

(иначе мы могли бы рассматривать функции –φ(t) и –ψ(t)). Итак,

φ′′(t) + b1(t)φ(t) ≡ 0,

ψ′′(t) + b2(t)ψ(t) ≡ 0.

Умножив первое тождество на ψ(t), а второе — на φ(t) и вычитая второе из первого, после несложных преобразований получим

d dt [φ′(t)ψ(t) – φ(t)ψ′(t)] = [b2(t) – b1(t)]φ(t)ψ(t).

Поскольку функция φ в точках t₁ и t₂ обращается в нуль, интегрирование последнего тождества по t в пределах от t₁ до t₂ приводит к равенству

φ′(t2)ψ(t2) – φ(t1)ψ′(t1) = ∫ t2 t1 [b2(t) – b1(t)]φ(t)ψ(t) dt.

По условию интеграл в правой части равенства неотрицателен. Левая же часть этого равенства отрицательна. Действительно, из условий

φ(t1) = φ(t2) = 0, φ(t) > 0 при t ∈ (t1, t2)

следует, что

φ′(t1) > 0, а φ′(t2) < 0.

Остается вспомнить, что ψ(t₁) и ψ(t₂) положительны. Полученное противоречие показывает, что наше предположение об отсутствии нулей функции ψ на [t₁, t₂] ложно.

Из утверждения задачи О20.3 в частности следует, что либо все решения уравнения (2) (а одновременно с ним и уравнения (1)) осциллируют (и в этом случае уравнения (1) и (2) называются осциллирующими), либо все они неосциллируют (и тогда уравнения называются неосциллирующими).

Задача О20.5. Сформулируйте и докажите аналог теоремы Штурма для уравнения (1).

Простым следствием теоремы Штурма является следующая

Теорема. Пусть в уравнении (2) коэффициент b₁ при всех t удовлетворяет неравенству

b1(t) ≥ ω2

(ω > 0). Тогда уравнение (2) является осциллирующим и, более того, расстояние между соседними нулями любого его решения не превосходит π/ω. Если, дополнительно,

b1(t) ≤ Ω2

при всех t, то расстояние между последовательными нулями любого решения не меньше, чем π/Ω.

Доказывается эта теорема сравнением уравнения (2) с уравнениями

x′′ + ω2x = 0   и   x′′ + Ω2x = 0,

решения которых легко выписываются.

Сравнение с уравнением

x′′ + α t2 = 0

(4)

приводит к следующему более тонкому утверждению:

Теорема. Если при достаточно больших t

b1(t) ≥ α t2     ( α > 1 4 ) ,

то уравнение (2) является осциллирующим. Если же

b1(t) ≤ α t2     ( α < 1 4 ) ,

при достаточно больших t, то уравнение (2) неосциллирующее.

Для  д о к а з а т е л ь с т в а  достаточно заметить, что уравнение (4) при α > 1/4 имеет общее решение вида

x(t) = {C1cos([(4α – 1)1/2ln t]/2) + C2sin ([(4α – 1)1/2ln t]/2)}t1/2,

являющееся осциллирующим, а при α < 1/4 это уравнение имеет общее решение вида

x(t) = C1t[1+(1–4α)1/2]/2 + C2t[1–(1–4α)1/2]/2,

являющееся неосциллирующим (докажите!)

Литературные указания. Изложение круга вопросов, связанных с осцилляцией решений можно найти, напр., в [Карташов — Рождественский, Петровский, Трикоми, Хартман].

Задачи. О20.6. Пусть в уравнении (1) коэффициенты a₁ и a₂ непрерывны. Покажите, что уравнение (1) и уравнение

d dt [p(t)y′] + q(t)y = 0,

(5)

в котором p(t) = exp(∫ a₁(t) dt, а q(t) = exp[∫ a₁(t) dt]a₀(t), эквивалентны. Форма (5) уравнения (1) называется дивергентной или самосопряженной. Для уравнений (5) и

d dt [p(t)y′] + s(t)y = 0,

докажите аналог теоремы Штурма: если q(t) ≤ s(t) при всех t, то между двумя последовательными нулями любого решения уравнения (1) содержится по крайней мере один нуль любого решения уравнения (2).

О20.7. Докажите теорему Штурма для уравнений в дивергентной форме в следующей более общей формулировке: пусть в уравнениях

d dt [p1(t)y′] + q1(t)y = 0,

(6)

d dt [p2(t)y′] + q2(t)y = 0,

(7)

коэффициенты p₁, p₂, q₁, q₂ непрерывны и удовлетворяют условиям

p1(t) ≥ p2(t) > 0,   q1(t) ≤ q2(t)

при всех t. Тогда между любыми двумя нулями каждого решения уравнения (6) есть хотя бы один нуль каждого решения уравнения (7).

О20.8. Докажите, что если в уравнении (2)

lim t→∞ b1(t) = 1,

то это уравнение является осциллирующим и, кроме того, расстояние между соседними нулями любого решения стремится к π, когда нули уходят в бесконечность.

О20.9. Пусть в уравнении (2)

lim t→∞ b1(t) = +∞.

Докажите, что это уравнение осциллирующее, причем, если t₁, t₂, ... — занумерованная по возрастанию последовательность (всех) нулей какого-либо решения этого уравнения, то |t_k – t_k+1| → 0 при k → ∞.

О20.10. Пусть в уравнении (2) коэффициент b₁ непрерывен на [α, β) и lim_t→βb₁(t) = +∞. Докажите, что множество нулей любого решения уравнения (2) образует сходящуюся к β последовательность. Покажите, что на любом отрезке [α₁, β₁] ⊂ [α, β) любое решение этого уравнения имеет лишь конечное число нулей.

О20.11. Пусть в уравнении (2) коэффициент b₁ монотонно возрастает, а t_k — занумерованная по возрастанию последовательность всех локальных экстремумов произвольного решения y этого уравнения. Докажите, что последовательность |y(t_k)| монотонно убывает. Если же b₁ убывает, то |y(t_k)| возрастает.

О20.12. Докажите, что если y₁ и y₂ — решения уравнений (2) и (3) соответственно, такие, что

y1(t0) = y2(t0),    y′1(t0)= y′2(t0),

то в условиях теоремы Штурма отношение y₁(t)/y₂(t) не убывает от t₀ до ближайшего нуля решения y₂.

О20.13. Уравнение

t2y′′ + ty′ + (t2 – ν2)y = 0

называется уравнением Бесселя, а его решения — функциями Бесселя. Заменой y√t = z оно приводится к виду

z′′ + ( 1 + 1 – 4ν2 4t2 ) z = 0.

Докажите, что расстояние между соседними нулями функции Бесселя не превосходит π при ν² ≤ 1/4 и не меньше π при ν² ≥ 1/4. Покажите, что уравнение Бесселя является осциллирующим при всех ν.

О20.14. Покажите, что расстояние между соседними нулями функции Бесселя стремится к π при стремлении нулей к +∞.

О20.15. Уравнение (2) называется уравнением без сопряженных точек на промежутке J, если любое его решение имеет на J не более одного нуля. Докажите, что уравнение (2) является уравнением без сопряженных точек в том и только том случае, когда оно имеет строго положительное на J решение.

О20.16. Докажите, что в последней теореме очерка оценки на b₁ можно ослабить до следующих

lim t→∞ t2b1(t) < 1 4   и    lim t→∞ t2b1(t) > 1 4 .

File based on translation from T_EX by T_TH, version 2.32.
Created 24 Feb 2000, 21:32.
Last modified 28 Apr 2002.