§ О14. Окрестность стационарной точки динамической системы

Вопрос о поведении траекторий в окрестности стационарной точки автономной системы обыкновенных дифференциальных уравнений удобно интерпретировать как классификационный, т. е. как вопрос о разбиении множества стационарных точек динамических систем на классы, в каждом из которых траектории в ее окрестности "ведут себя одинаково"; последующее исследование "простейшего" представителя такого класса дает информацию обо всем классе. В свою очередь, этот вопрос естественным образом сводится к вопросу о выборе отношения эквивалентности, осуществляющего это разбиение на классы. Выбирая отношение эквивалентности, приходится решать две противоположные задачи. С одной стороны, это отношение должно быть достаточно грубым, чтобы получившееся множество классов было обозримым и системы из разных классов были достаточно разными. С другой стороны, оно должно быть достаточно тонким, чтобы вместе с водой не выплеснуть и ребенка.

Эффективным здесь оказывается следующее отношение эквивалентности. Две динамические системы

x′ = f1(x)  и  x′ = f2(x)

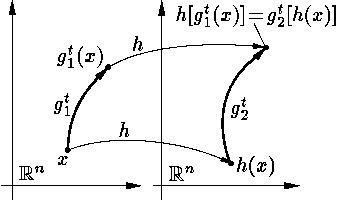
(f₁, f₂: Rⁿ → Rⁿ) с нулевой стационарной точкой называются локально топологически эквивалентными, если найдется такой определенный в некоторой окрестности нуля фазового пространства гомеоморфизм h такой, что

h[gt1(x)]= gt2[h(x)]

при всех t и x, при которых обе части тождества имеют смысл; здесь gt1и gt2— соответствующие операторы сдвига. Таким образом, гомеоморфизм h переводит траектории первой системы в траектории второй, причем, согласованно (см. рис. 1). Если h определен на всем фазовом пространстве, то слово "локально" в определении локальной топологической эквивалентности опускают.

Рис. 1.

Задача О14.1. Докажите, что это действительно отношение эквивалентности, т. е. рефлексивное симметричное транзитивное отношение.

Начнем с задачи классификации стационарных точек линейных систем. Линейная система

x′ = Ax

называется гиперболической, если матрица A не имеет собственных значений на мнимой оси. Основной результат в этой области —

Теорема о топологической эквивалентности линейных гиперболических систем. Две гиперболические системы x′ = A₁x и x′ = A₂x топологически эквивалентны, если и только если числа n_–(A₁) и n_–(A₂) собственных значений с отрицательной вещественной частью с учетом кратности (а следовательно, и числа n₊(A₁) и n₊(A₂) собственных значений с положительной вещественной частью) матриц A₁ и A₂ совпадают: n _– (A₁) = n _– (A₂), n₊(A₁) = n₊(A₂).

Доказательство этой теоремы выходит за рамки очерка, мы лишь поясним ее на примерах и дадим идею доказательства. Например, из нее вытекает, что двумерные гиперболические системы разбиваются на три топологически не эквивалентных класса: а) устойчивые узлы и фокусы; б) седла; в) неустойчивые узлы и фокусы (см. рис. 2). На рис. 3 изображены представители четырех классов топологической эквивалентности трехмерных гиперболических систем.

Рис. 2.

Рис. 3.

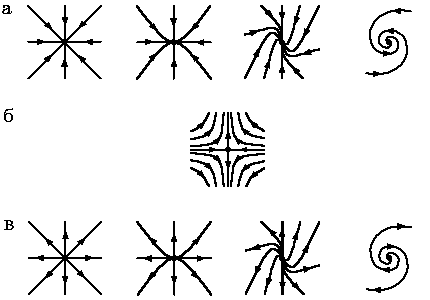
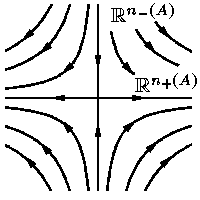
Теорема утверждает, что любая гиперболическая динамическая система x′ = Ax топологически эквивалентна следующей системе, описывающей по определению стандартное многомерное седло (см. рис. 4),

y′ = –y,    z′ = z,

где y ∈ Rn–(A), а z ∈ Rn+(A). Подпространство y ∈ Rn–(A) пространства Rn называется входящим усом (или сепаратрисой) седла, а z ∈ Rn+(A) — выходящим.

Рис. 4.

Задача О14.2. Покажите, что две линейные системы

{ y′ = A1y, z′ = B1z,   и   { y′ = A2y, z′ = B2z,

(y ∈ Rⁿ, z ∈ R^m) топологически эквивалентны, если попарно топологически эквивалентны системы y′ = A₁y,  y′ = A₂y  и  z′ = B₁z,  z′ = B₂z.

Поясним основную идею доказательства теоремы об эквивалентности на примере. Рассмотрим две двумерные динамические системы

x′1= –x1 + x2,    x′2= –x1 – x2

(1)

и

x′1= –x1,    x′2= –x2.

(2)

Стационарная точка первой из них — устойчивый фокус, а второй — устойчивый узел. Обозначим через gt1и gt2 операторы сдвига по траекториям систем (1) и (2) соответственно. Гомеоморфизм в данном случае строится так. Для любого x ∈ R2 обозначим через tx время, за которое оператор сдвига gt1переводит точку x в точку y, являющуюся пересечением траектории t → gt1(x) и единичной сферы S в R2.Положим, по определению,

h(x) = gtx1[g–tx2(x)]

(3)

(см. рис. 5; на нем I — тождественное отображение в R²).

Рис. 5.

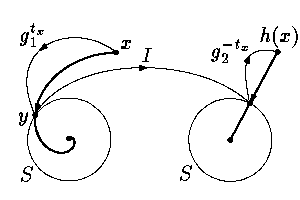
Задача О14.3. Докажите, что h осуществляет топологическую эквивалентность систем (1) и (2).

В ситуации неустойчивых фокуса и узла h строится аналогично. В общем случае в качестве S нужно брать поверхность уровня некоторой функции Ляпунова. Произвольную гиперболическую систему можно представить в виде системы двух уравнений со спектрами, лежащими соответственно в правой и левой полуплоскостях. Для каждого из них гомеоморфизм, приводящий эти уравнения к уравнениям x′ = x и x′ = –x, строится по описанной выше схеме. Затем остается воспользоваться утверждением задачи 3.

Несколько слов о выборе отношения эквивалентности. Если гомеоморфизм h в вышеприведенном определении линеен (является диффеоморфизмом), то говорят, что динамические системы линейно (дифференцируемо) эквивалентны.

Задача О14.4. Докажите, что две динамические системы дифференцируемо эквивалентны тогда и только тогда, когда они линейно эквивалентны.

Задача О14.5. Покажите, что если линейные системы x′ = A₁x и x′ = A₂x линейно эквивалентны, то операторы A₁ и A₂ подобны, т. е. существует невырожденное линейное отображение h: Rⁿ → Rⁿ такое, что A₁ = hA₂h^–1.

Таким образом, необходимым условием линейной эквивалентности двух линейных систем является совпадение их спектров. Например, системы x′ = x и x′ = αx не являются линейно (и следовательно дифференцируемо) эквивалентными при всех α ≠ 1, откуда, в частности, следует, что множество классов линейно (или дифференцируемо) эквивалентных систем континуально.

Задача О14.6. Докажите, что системы (1) и (2) не являются линейно эквивалентными.

Поэтому определенный формулой (3) гомеоморфизм h принципиально не является линейным (и, более того, не является диффеоморфизмом).

Перейдем к вопросу о структуре окрестности стационарной точки нелинейных динамических систем. Мы ограничимся случаем динамической системы с дифференцируемой правой частью

x′ = f(x)

(4)

(f ∈ C¹(Rⁿ, Rⁿ), f(0) = 0), причем будем предполагать, что линеаризованная в нулевой стационарной точке система

x′ = Ax

(5)

(A = f ′(0)) гиперболическая. В этом случае ответ на вопрос о поведении траекторий в окрестности нулевой стационарной точки дает фундаментальная

Теорема Гробмана — Хартмана. Динамическая система (4) локально топологически эквивалентна своей линейной части (5).

Таким образом, в описанной ситуации динамическая система локально топологически эквивалентна стандартному многомерному седлу (см. рис. 6).

Рис. 6.

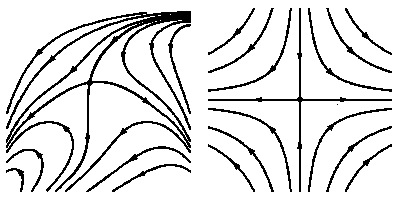
Если линеаризованная система не гиперболична, то заключение о поведении траекторий системы (4) без дополнительной информации сделать нельзя.

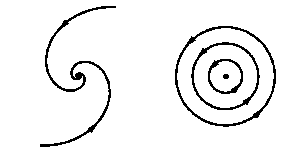
Задача О14.7. Докажите, что система

{ x′1= –x2 + x1(x21 + x22), x′2= x1 + x2(x21 + x22)

и ее линеаризация в нуле не являются локально топологически эквивалентными (см. рис. 7).

Рис. 7.

Еще один пример принципиально различного поведения систем с одинаковой (но не гиперболичной) линейной частью изображен на рис. 8.

Рис. 8.

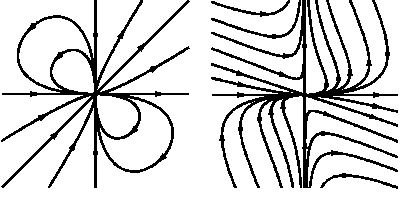
Про динамические системы на плоскости, линейная часть которых представляет собой центр известно, что их фазовый портрет в окрестности стационарной точки является либо фокусом, либо центром. Для уточнения типа стационарной точки в этом случае необходимо привлекать информацию о старших членах в разложении правых частей уравнений в ряды Тейлора. Задача о выяснении типа стационарной точки с помощью конечного числа операций над коэффициентами этих рядов называется проблемой центра — фокуса.

Литературные указания. И опять, как в предыдущих двух очерках, ограничимся указанием на распространенные учебники и монографии [Арнольд, Арнольд, Бибиков, Итоги науки и техники..., Коддингтон — Левинсон, Немыцкий — Степанов, Палис — ди Мелу, Хартман,

Эрроусмит — Плейс].

Задачи. О14.8. Докажите, что линейная система x′ = Ax гиперболична тогда и только тогда, когда ω-предельное множество любой траектории либо {0}, либо пусто.

О14.9. Пусть A — произвольный класс топологической эквивалентности во множестве линейных гиперболических систем. Докажите, что множество операторов A таких, что (x′ = Ax) ∈ A открыто в пространстве линейных ограниченных операторов L(Rⁿ, Rⁿ). Это означает, что малые возмущения не выводят из класса эквивалентности гиперболических систем.

О14.10. Покажите, что класс линейной эквивалентности не является открытым в указанном в предыдущей задаче смысле.

О14.11. Докажите, что системы

x′1= a1x1,    x′2= a2x2

(a₁, a₂ ≠ 0) и

x′1= b1x1,    x′2= b2x2

линейно эквивалентны в том и только том случае, если либо a₁ = b₁, a₂ = b₂, либо a₁ = b₂, a₂ = b₁.

О14.12. Докажите, что системы

{ x′1= x1, x′2= x1 + x2   и   { x′1= x1, x′2= x2

не являются линейно эквивалентными, хотя их спектры совпадают.

О14.13. Пусть все собственные значения систем x′ = A₁x и x′ = A₂x являются простыми, а операторы A₁ и A₂ подобны. Докажите, что эти динамические системы линейно эквивалентны.

О14.14. Покажите, что две динамические системы x′ = f₁(x) и y′ = f₂(y) дифференцируемо эквивалентны в том и только том случае, если существует невырожденная дифференцируемая замена переменных y = h(x), переводящая первую систему во вторую.

О14.15. Покажите, что приведенные на рис. 8 системы не являются локально топологически эквивалентными.

О14.16. Докажите, что положение равновесия x₁ = k₂/ε₂, x₂ = k₁/ε₁ системы хищник — жертва

x′1= k1x1 – ε1x1x2,

x′2= –k2x2 + ε2x1x2,

(k_i, ε_i > 0, i = 1 ,2) является центром, т. е. эта система локально топологически эквивалентна линейной системе, описывающей центр.

О14.17. Докажите, что динамическая система

x′1= ax1,    x′2= bx2 + εx1x3,    x′3= (b – a)x3

(a > a – b > 0, ε ≠ 0) и ее линейная часть

x′1= ax1,    x′2= bx2,    x′3= (b – a)x3

не являются локально дифференцируемо эквивалентными (Хартман). Являются ли они локально топологически эквивалентными?.

О14.18. Докажите, что динамические системы, описывающие линейный осциллятор без трения и линейный осциллятор с трением не являются топологически эквивалентными.

File based on translation from T_EX by T_TH, version 2.32.
Created 27 Jan 2000, 09:17.
Last modified 25 Apr 2002.