§ О15. Грубые системы

Грубые системы — это системы дифференциальных уравнений, у которых топологическое поведение траекторий не меняется при малых возмущениях правой части. Согласно общепринятой точке зрения только грубые системы могут описывать реальные процессы. Нельзя доверять математической модели, резко меняющей свое поведение при малом изменении входящих в нее параметров (которые в реальности никогда не могут определяться точно). В некотором смысле рассматриваемые ниже вопросы являются глобальными аналогами рассматривавшихся в очерке О14 вопросов локальной теории дифференциальных уравнений.

Перейдем к точным определениям. Поскольку традиционно теория грубых систем излагается для дифференциальных уравнений на многообразиях, мы также следуем этой традиции. Кроме того, все многообразия предполагаются компактными и поэтому не возникает вопросов, связанных с продолжимостью решений. Итак, все рассмотрения ведутся на Cr+1-гладком компактном многообразии M. Начнем с определения понятия эквивалентности на множестве дифференциальных уравнений, которое позволяет разбивать это множество на классы с одинаковым поведением траекторий (ср. с вводной частью очерка О14). Два дифференциальных уравнения (динамических системы) на M (а также определяющие их векторные поля f1, f2: M → TM) называются орбитально топологически эквивалентными, если найдется гомеоморфизм h: M → M, переводящий траектории уравнения x′ = f1(x) в траектории уравнения x′ = f2(x) и сохраняющий направление движения по ним. Последнее, по определению, означает, что (мы обозначаем через gt1и gt2 потоки, т. е. операторы сдвига за время от нуля до t по траекториям соответствующего уравнения) для любых x ∈ M и t > 0 найдется τ > 0 такое, что h[gt1(x)]= gτ2[h(x)] (см. рис. 1). Если τ = t, то уравнения называются топологически эквивалентными. Это понятие есть точный глобальный аналог понятия локальной топологической эквивалентности.

Рис. 1.

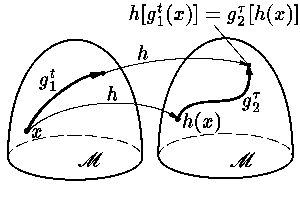
Задача О15.1. Докажите, что определенные выше понятия действительно являются отношениями эквивалентности.

Задача О15.2. Покажите, что системы дифференциальных уравнений на R² (не обращайте внимания на некомпактность R²)

{ x′1 = x1, x′2 = x2   и   { x′1 = x1 + x2, x′2 = –x1 + x2

орбитально топологически эквивалентны и более того, топологически эквивалентны.

Задача О15.3. Покажите, что системы дифференциальных уравнений на R³

{ x′1= –x2, x′2= x1   и   { x′1= –2x2, x′2= 2x1

орбитально топологически эквивалентны, но не топологически эквивалентны.

По определению, пространство C^r(M, N) состоит из C^r-гладких векторных полей f: M → N; близость полей f₁ и f₂ в топологии этого пространства есть равномерная на M близость полей f₁ и f₂ и всех их производных до порядка r включительно.

Суть введенного А.А. Андроновым и А.С. Понтрягиным понятия грубой системы такова: малое возмущение грубой системы переводит систему в орбитально топологически ей эквивалентную. Точнее, динамическая система

x′ = f(x),

(1)

отвечающая C^r-гладкому векторному полю f: M → TM, называется грубой (или структурно устойчивой), если:

(а) найдется окрестность V_f точки f в пространстве C^r(M, TM) такая, что при всех f₁ ∈ V_f уравнение x′ = f₁(x) орбитально топологически эквивалентно уравнению (1);

(б) гомеоморфизм, осуществляющий эквивалентность, близок к тождественному в топологии пространства C⁰(M, M).

Говорят также и о грубом векторном поле f. Если в этом определении опустить требование (б), то уравнение (1) называется грубым по Пейксото. До сих пор не известно являются ли понятия грубости по Андронову — Понтрягину и грубости по Пейксото различными понятиями.

Задача О15.4. Покажите, что система, отвечающая нулевому векторному полю на произвольном гладком многообразии, не является грубой.

Задача О15.5. Докажите, что система x′1= x1, x′2= x2 на R2 является грубой.

Следует подчеркнуть, что структурная устойчивость, вообще говоря, не сохраняется при переходе к орбитально топологически эквивалентной системе (см. задачу О15.15). Поэтому в одном и том же классе орбитальной топологической эквивалентности могут содержаться как грубые, так и негрубые системы. Разумеется, траектории этих систем с топологической точки зрения ведут себя одинаково.

В общем случае исследование дифференциального уравнения на грубость сложно и требует развитой техники. Мы опишем (без доказательств) грубые дифференциальные уравнения (векторные поля) на одномерной и двумерной сферах, а также на двумерном торе.

Стационарная (особая) точка x₀ уравнения x′ = f(x) на окружности S¹ называется невырожденной, если касательное отображение df(x₀) в этой точке отлично от нуля. Легко видеть, что любая невырожденная особая точка изолирована, т. е. в ее окрестности нет других стационарных точек.

Задача О15.6. Покажите, что множество C^r-гладких векторных полей f: S¹ → TS¹ = R¹, все стационарные точки которых невырождены, образуют открытое множество в C^r(S¹, TS¹).

Несложно доказывается следующая

Теорема о грубых системах на окружности. Уравнение (1) на S¹ является грубым в том и только том случае, если все его стационарные точки невырождены.

Задача О15.7. Покажите, что два дифференциальных уравнения на S¹ с невырожденными особыми точками орбитально топологически эквивалентны в том и только том случае, если они имеют одинаковое число особых точек.

С помощью теоремы Сарда (см. любой продвинутый курс математического анализа) можно доказать, что множество грубых векторных полей на S¹ всюду плотно в пространстве всех C^r-гладких векторных полей на S¹.

Описание множества всех грубых дифференциальных уравнений на двумерной сфере S² сложнее. Стационарная точка x₀ дифференциального уравнения (1) на сфере S² называется невырожденной (или обобщенным седлом ), если касательное отображение df(x₀) в этой точке не имеет нулевого собственного значения. Замкнутая траектория (цикл) этого уравнения называется невырожденной, если касательное к отображению последования отображение не имеет единичного собственного значения. Фазовая траектория называется входящей сепаратрисой (обобщенного) седла x₀, если она стремится к x₀ при t → +∞ и, соответственно, выходящей сепаратрисой седла x₀, если она стремится к x₀ при t → –∞. Все грубые системы на S² описывает следующая

Теорема о грубых системах на двумерной сфере. Уравнение (1) на S² является грубым тогда и только тогда, когда выполнены следующие условия:

(а) все стационарные точки невырождены;

(б) все циклы невырождены;

(в) ни одна выходящая сепаратриса седла не является входящей сепаратрисой данного или другого седла.

Доказательства этой и нижеследующей теоремы достаточно громоздки и поэтому опускаются.

Перейдем к уравнениям на торе. Пусть в уравнении (1) f: T² → TT² (T² — двумерный тор) и пусть соответствующее уравнение на плоскости

x′1= f1(x1, x2),   x′2= f2(x1, x2)

таково, что f₁(x₁, x₂) ≠ 0. Числом вращения μ(f) уравнения (1) на торе T² называется число вращения уравнения

x′1= 1,    x′2= f2(x1, x2)/f1(x1,x2).

Задача О15.8. Покажите, что обмотка тора не является грубой вне зависимости от того рациональна она или иррациональна.

Теорема о грубых системах на двумерном торе. Удовлетворяющее описанному выше условию уравнение (1) на торе является грубым, если и только если μ(f) рационально и все его циклы невырождены.

В случае, когда размерность многообразия M мала (≤ 2) грубые системы образуют во множестве всех динамических систем на M открытое всюду плотное множество. На многообразиях больших размерностей это не так. Известны негрубые системы, в некоторой окрестности которых нет ни одной грубой системы!

На многообразиях размерности 1 и 2 грубые системы допускают описание в терминах качественного поведения траекторий. Именно, грубыми системами на таких многообразиях являются системы, удовлетворяющие следующим требованиям:

(а) стационарные точки и циклы невырождены;

(б) инвариантные многообразия стационарных точек и циклов (это входящие и выходящие усы обобщенных седел и притягивающие и отталкивающие инвариантные многообразия циклов) пересекаются трансверсально, т. е. под ненулевым углом;

(в) все остальные траектории при t → +∞ и при t → –∞ стремятся к стационарным точкам или циклам.

Динамические системы, удовлетворяющие требованиям (а) – (в), называются системами Морса — Смейла. На многообразиях бóльших размерностей аналогичное описание грубых систем неизвестно.

Литературные указания. Теория грубых систем восходит к работам А.А. Андронова и А.С. Понтрягина. Современное изложение теории структурной устойчивости см., напр., в [Арнольд, Голубицкий — Гийемин, Итоги науки и техники..., З. Нитецки, Палис — ди Мелу].

Задачи. О15.9. Покажите, что если два дифференциальных уравнения на M орбитально топологически эквивалентны, то траектория первого уравнения, проходящая через точку x ∈ M, замкнута в том и только том случае, если замкнута траектория второго уравнения, проходящая через точку h(x).

О15.10. В условиях предыдущей задачи покажите, что для любой траектории T_φ первого уравнения h[Ω(T_φ)] = Ω[h(T_φ)] (здесь Ω(T_φ) и Ω[h(T_φ)] — ω-предельные множества траекторий T_φ и h(T_φ) первого и второго уравнений, соответственно).

О15.11. Покажите, что число стационарных точек грубого уравнения на окружности четно.

О15.12. Покажите, что мощность множества классов эквивалентности дифференциальных уравнений на окружности не меньше мощности множества классов гомеоморфных компактных подмножеств S¹.

О15.13. C^r-диффеоморфизм g: M → M называется грубым, если для любого достаточно близкого к нему в C^r(M, M) диффеоморфизма f найдется гомеоморфизм f: M → M такой, что hf = gh, т. е. f = h^–1gh. Пусть уравнение x′ = f(x) на S¹ грубо и имеет по крайней мере одну особую точку. Пусть g = g¹ — оператор сдвига по траекториям этого уравнения за единичное время. Покажите, что диффеоморфизм g грубый.

О15.14. Приведите пример грубого дифференциального уравнения на S¹, у которого оператор сдвига g = g¹ за единичное время не является грубым.

О15.15. Приведите пример негрубой динамической системы на двумерной сфере S² орбитально топологически эквивалентной грубой динамической системе на S². (Указание: грубая система порождена векторным полем, направленным вдоль меридианов, с экспоненциально устойчивым северным полюсом и экспоненциально неустойчивым южным; негрубая же система получается из первой изменением длины векторов первого поля в окрестности южного полюса (при сохранении их направления) таким образом, чтобы южный полюс стал неустойчивой (отталкивающей) вырожденной стационарной точкой: тогда под воздействием малого возмущения в ее окрестности может появиться цикл).

О15.16. Докажите, что нарушение хотя бы одного из условий (а) — (в) теоремы о грубых системах на двумерной сфере влечет негрубость уравнения (1).

О15.17. Покажите, что стационарные точки грубой системы невырождены.

О15.18. Докажите, что циклы грубой системы невырождены.

О15.19. Докажите, что грубая система на компактном многообразии имеет не более чем конечное число стационарных точек.

О15.20. Докажите, что грубая система на компактном многообразии имеет не более, чем конечное число циклов.

File based on translation from T_EX by T_TH, version 2.32.
Created 28 Jan 2000, 10:08.
Last modified 26 Apr 2002.