§ О13. Линейные автономные системы на плоскости. Линейная классификация

Предмет данного очерка совершенно элементарен. Мы описываем полную линейную классификацию двумерных систем с постоянными коэффициентами (под линейной классификацией понимается разбиение множества таких систем на классы, инвариантные относительно линейного преобразования фазового пространства). Одна из целей очерка — описание терминологии, связанной с поведением траекторий (т. е. с фазовыми портретами).

Итак, рассматривается двумерная линейная динамическая (автономная) система

x′ = Ax,

(1)

где A — 2×2-матрица с постоянными коэффициентами. Линейное преобразование P: R² →R² с вещественными коэффициентами переводит (1) в систему

y′ = By,

(2)

Рис. 1.

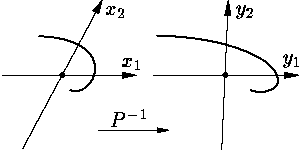
где B = P^–1AP, а y = P^–1x. Это же преобразование переводит фазовые траектории системы (2) в фазовые траектории системы (1) (см. рис. 1). Преобразование P будет выбираться в зависимости от собственных значений λ₁, λ₂ матрицы A.

Если λ₁, λ₂ вещественны, то в качестве P возьмем такую матрицу, чтобы B была жордановой. В этом случае мы будем различать два типа матрицы B:

B = B1 = ( λ1 0 0 λ1 )  и  B = B2 = ( λ1 1 0 λ1 ) .

Пусть теперь λ₁ = α + iβ, λ₂ = λ₁ = α – iβ (β > 0) — комплексные собственные значения матрицы A, u + iv — собственный вектор матрицы A, отвечающий собственному значению λ₁.

Задача О13.1. Покажите, что (вещественные) векторы u и v линейно независимы.

Заметим, что

Au + iAv = A(u + iv) = (α + iβ) (u + iv) = αu – βv + i(βu + αv)

и, следовательно,

Au = αu – βv,   Av = βu + αv.

Преобразование P на векторах канонического базиса определим равенствами

Pe1 = u,   Pe2 = v

и продолжим его на все R² по линейности. Простым подсчетом проверяется, что B имеет вид

B = B3 = ( α β –β α ) .

Задача О13.2. Проверьте.

Таким образом, (вещественным) линейным преобразованием P произвольная матрица A может быть приведена к одной из (вещественных) матриц B₁, B₂ или B₃.

Далее, заменой времени t = pτ и неизвестной функции z(τ) = y(pτ) система (2) приводится к системе

z′ = Cz,

(3)

где C = pB.

Задача О13.3. Покажите.

Описанная замена не меняет фазовых траекторий системы; изменяется лишь (в p раз) скорость движения по ним. Если p < 0, то меняется и направление движения. В дальнейшем мы будем считать, что p > 0. Очевидно, собственные значения μ матрицы C и собственные значения λ матрицы B (являющиеся также собственными значениями матрицы A) связаны соотношением μ = pλ.

В случае B = B₁ описанную замену мы применим следующим образом. Если среди (вещественных) собственных значений есть положительное (не ограничивая общности будем считать, что λ₁ — наибольшее собственное значение), то положим p = λ₁ ^{– 1}. Матрица C в этом случае будем иметь вид

C = C1 = ( 1 0 0 k ) ,

где k = pλ₂ ≤ 1. Если λ₁ = λ₂ = 0, то положим p = 1. В этом случае матрица C, очевидно, нулевая:

C = C2 = ( 0 0 0 0 ) .

Наконец, если λ1 и λ2 неположительны и если меньшее из них (пусть, для определенности, это λ1) отрицательно, то положим p = –λ1–1. Матрица C при этом будет иметь вид

C = C3 = ( –1 0 0 k ) .

где k = pλ₂ ∈ [0, 1].

В случае B = B₂ в зависимости от знака λ₁ подберем p так, чтобы матрица C имела один из следующих трех видов:

C = C4 = ( 1 k 0 1 )

(λ1 > 0, p = λ1–1, k = p > 0),

C = C5 = ( 0 k 0 0 )

(λ₁ = 0, p = 1),

C = C6 = ( –1 k 0 –1 )

(λ1 < 0, p = –λ1–1, k = p > 0).

Наконец, в случае B = B₃ вид матрицы C, как и в предыдущем случае, определим в соответствии со знаком числа α:

C = C7 = ( 1 k –k 1 )

(α > 0, p = α^–1, k = pβ > 0),

C = C8 = ( 0 k –k 0 )

(α = 0, p = 1, k = β > 0),

C = C9 = ( –1 k –k –1 )

(α < 0, p = –α^–1, k = pβ > 0).

Теперь мы опишем поведение траекторий (фазовый портрет) системы (3) с каждой из матриц C₁, ..., C₉.

В случае C = C₁ решения системы (3), очевидно, таковы

z1 = c1et,    z2 = c2ekt.

(4)

Траектории симметричны относительно осей координат и поэтому достаточно изучить их поведение в первом квадранте, т. е. только те, для которых c1, c2 ≥ 0. Кроме того, поскольку каждая из осей координат является траекторией, можно считать, что c1, c2 > 0. Избавляясь от t в (4), получаем соотношение z2 = czk (c = c2/c1k), описывающее фазовые траектории. Если k = 1, то фазовые траектории представляют собой лучи, выходящие из начала координат; при t → +∞ фазовая точка "уходит на бесконечность" (см. рис. 2). Такая фазовая картина называется неустойчивым вырожденным узлом.

Рис. 2.

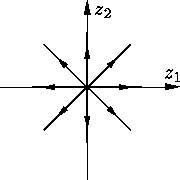
Если k ∈ (0, 1), то фазовые траектории представляют собой степенные параболы; при t → +∞ фазовая точка по-прежнему уходит на бесконечность (см. рис. 3). Такая фазовая картина называется неустойчивым узлом.

Рис. 3.

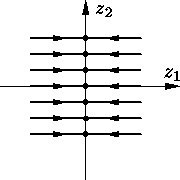
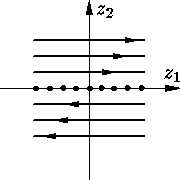
Если k = 0, то, очевидно, все траектории параллельны оси z₁, вся ось z₁ состоит из положений равновесия, траектории (за исключением положений равновесия) уходят на бесконечность (см. рис. 4). Этот вырожденный случай, как и ряд других, описываемых ниже, специального названия не имеет.

Рис. 4.

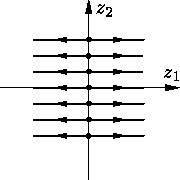
Наконец, если k < 0, то фазовые траектории представляют собой степенные гиперболы z2 = cz1k, движение по ним в первом квадранте происходит по правилу "вниз-вправо". Вблизи оси z2 фазовая точка движется "почти параллельно" оси, а затем, приблизившись к оси z1, "вдоль" нее уходит при t → +∞ в бесконечность (см. рис. 5). Такая фазовая картина называется седлом.

Рис. 5.

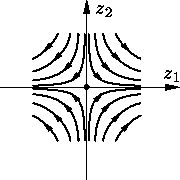
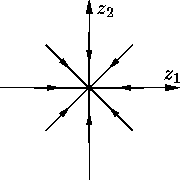
В вырожденном случае C = C₂, очевидно, каждая точка фазовой плоскости является положением равновесия: траектория, начинаясь в этой точке "стоит" в ней все время (см. рис. 6).

Рис. 6.

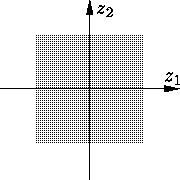
В случае C = C3 решение задается формулами z1 = c1e–t, z2 = c2ekt. Соответствующие траектории z2 = cz1–k отличаются от случая C = C1, k ∈ [0, 1] лишь направлениями движения по ним. При k = 0 (см. рис. 7) картина аналогична изображенной на рис. 4.

Рис. 7.

При k ∈ (–1, 0) (см. рис. 8) фазовый портрет аналогичен изображенному на рис. 3, но фазовая точка при t → +∞ стремится к нулевому состоянию равновесия. Поэтому фазовая картина называется устойчивым узлом.

Рис. 8.

Фазовый портрет при k = –1 называется устойчивым вырожденным узлом (см. рис. 9).

Рис. 9.

В случае C = C₄ система (3) имеет вид

z′1= z1 + kz2,    z′2= z2.

Решение выписывается в явном виде:

z1 = c1et + c2ktet,    z2 = c2et.

Очевидно, множество траекторий симметрично относительно начала координат. Поэтому достаточно изучить поведение траекторий в верхней полуплоскости (c₂ ≥ 0). Избавляясь от t в последних равенствах, получим

z1 = c1 c2 z2 + c1kz2ln z2 c2 .

Задача О13.4. Покажите, что фазовый портрет имеет вид, изображенный на рис. 10).

Рис. 10.

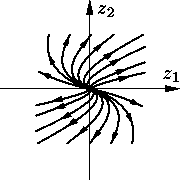
Фазовая картина в этом случае также называется неустойчивым вырожденным узлом.

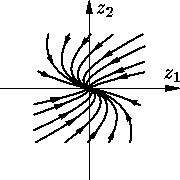
В случае C = C₅ решение имеет вид z₁ = c₁ + c₂kt, z₂ = c₂. Все траектории параллельны оси z₁, каждая точка которой является положением равновесия. Чем ближе находится траектория к оси z₁, тем с меньшей скоростью движется по ней фазовая точка, причем, в верхней полуплоскости точка движется вправо, а в нижней — влево (рис. 11).

Рис. 11.

Случай C = C₆ (устойчивый вырожденный узел) отличается от случая C = C₄ только направлением движения фазовой точки по траекториям и, таким образом, свойствами устойчивости нулевого положения равновесия (см. рис. 12).

Рис. 12.

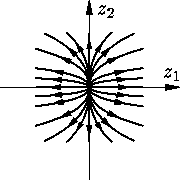
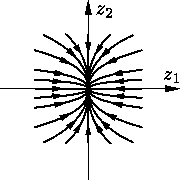
В случае C = C₇ общее решение системы (3) имеет вид

z1 = et(c1cos kt + c2sin kt), z2 = et(c2cos kt – c1sin kt).

Положим z = (c12+ c22)1/2. Тогда, как легко видеть,

z1 = retcos(kt + φ0),    z2 = –retsin(kt + φ0),

где cos φ₀ = c₁/r, sin φ₀ = –c₂/r. Переходя к полярным координатам ρ, φ, получаем

ρ(t) = ret,    φ(t) = –kt – φ0.

Отсюда следует, что траектории представляют собой логарифмические спирали. Фазовая точка движется по ним по часовой стрелке и при t → +∞ уходит в бесконечность (см. рис. 13). Фазовая картина называется неустойчивым фокусом.

Рис. 13.

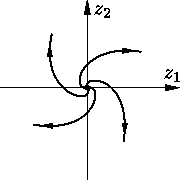
В случае C = C₈ аналогичные преобразования приводят к представлению решения в виде

ρ(t) = r,    φ(t) = –kt – φ0.

Поэтому траектории представляют собой окружности с центром в начале координат, фазовая точка движется по ним по часовой стрелке (см. рис. 14). Фазовая картина называется центром.

Рис. 14.

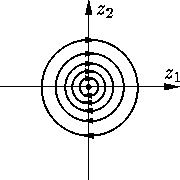
Наконец, при C = C₉ решение имеет вид

ρ(t) = ret,    φ(t) = –kt – φ0.

Траектории — логарифмические спирали, траектория движется по ним по часовой стрелке и при t → +∞ стремится к нулевому положению равновесия (см. рис. 15). Фазовая картина — по определению устойчивый фокус.

Рис. 15.

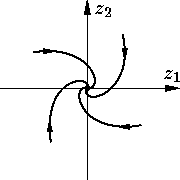
В заключение хотим предостеречь читателя от мысли, что в последних трех случаях фазовая точка исходной системы (1) также всегда движется по часовой стрелке. На самом деле замена x = Py может (в зависимости от знака det P) менять ориентацию фазовой плоскости и поэтому фазовая точка системы (1) движется либо в том же направлении, что и фазовая точка системы (3), либо в противоположном. Неизменным при этом остается лишь стремление при t → +∞ фазовой точки к нулю или бесконечности (см. рис. 16).

Рис. 16.

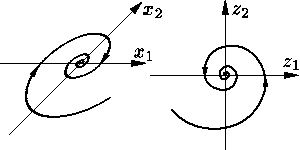
Литературные указания. Исследование фазовых портретов двумерных линейных систем с постоянными коэффициентами можно найти фактически в каждом учебнике по обыкновенным дифференциальным уравнениям; см., напр., [Арнольд, Бибиков, Карташов — Рождественский, Петровский, Понтрягин, Тихонов — Васильева — Свешников, Федорюк, Хартман].

Задачи. О13.5. Докажите, что если фазовый портрет (1) есть устойчивый или неустойчивый узел, седло, устойчивый или неустойчивый фокус, то любая достаточно близкая к ней линейная автономная система (т. е. система с близкой к A матрицей) имеет соответствующий фазовый портрет.

О13.6. Докажите, что в сколь угодно малой окрестности системы, являющейся центром, есть как системы, являющиеся устойчивым фокусом, так и системы, являющиеся неустойчивым фокусом.

File based on translation from T_EX by T_TH, version 2.32.
Created 21 Jan 2000, 02:43.
Last modified 25 Apr 2002.