§ О9. Уравнения в частных производных первого порядка

Линейным дифференциальным уравнением в частных производных первого порядка называется уравнение вида

f1(x) ∂u ∂x1  + ... + fn(x) ∂u ∂xn  = 0,

(1)

в котором f₁, ..., f_n — заданные непрерывные скалярные функции, определенные в области D(f) пространства Rⁿ. Решением уравнения (1) называется определенная в подобласти D области D(f) скалярная функция u, имеющая частные производные первого порядка по всем переменным и обращающая уравнение (1) в тождество относительно x = (x₁, ..., x_n) ∈ D. График решения u = u(x₁, ..., x_n) в пространстве R×Rⁿ называется интегральной поверхностью уравнения (1).

Как уже указывалось в очерке О8, автономные первые интегралы системы обыкновенных дифференциальных уравнений

x′ = f(x)

(2)

(здесь f = (f₁, ..., f_n): D(f) → Rⁿ) и только они являются решениями уравнения (1). Таким образом, траектории системы (2) являются линиями уровня интегральной поверхности уравнения (1) (см. рис. 1). Эти траектории называются характеристиками уравнения (1).

Рис. 1.

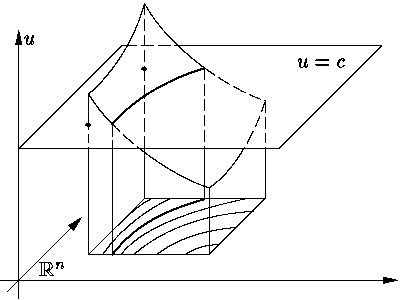
Таким образом, задача о нахождении решений уравнения (1) сводится к задаче о нахождении первого интеграла системы (2). Полный первый интеграл этой системы играет при этом роль "базиса" во множестве всех решений. Более подробно. Пусть функция f = (f₁, ..., f_n) непрерывно дифференцируема, а ее производная удовлетворяет условию Липшица. Пусть, кроме того, f(x₀) ≠ 0. Тогда в силу теоремы об автономных первых интегралах в некоторой окрестности D точки x₀ существует (n – 1)-мерный невырожденный автономный первый интеграл V(x) системы (2). Из этой же теоремы следует, что любое решение u уравнения (1) (т. е. автономный скалярный первый интеграл уравнения (2)) может быть записан в окрестности D в виде

u(x) = F[V(x)],

где F: R^n–1 → R — некоторая (своя для каждого решения) непрерывно дифференцируемая функция.

Более сложный объект представляет собой т. н. квазилинейное дифференциальное уравнение в частных производных первого порядка — уравнение вида

f1(x, u) ∂u ∂x1  + ... + fn(x, u) ∂u ∂xn  = fn+1(x, u),

(3)

в котором f = (f₁, ..., f_n+1): D(f) ⊂ Rⁿ⁺¹ → Rⁿ⁺¹ — заданная непрерывная функция. Решение и интегральная поверхность уравнения (3) определяются аналогично. Отметим, что понятие решения включает в себя и требование, чтобы (x, u(x)) ∈ D(f) при всех x ∈ D = D(u). Подчеркнем, что в отличие от уравнения (1), уравнение (3) линейным не является. В частности, линейная комбинация решений не обязательно является его решением.

С уравнением (3) тесно связано следующее линейное(!) дифференциальное уравнение в частных производных первого порядка

f1(x, u) ∂v ∂x1  + ... + fn(x, u) ∂v ∂xn  + fn+1(x, u) ∂v ∂u  = 0

(4)

и соответствующая ему ((n + 1)-мерная) система обыкновенных дифференциальных уравнений

x′ = f(x, u), u′ = fn+1(x, u),

(5)

где f = (f₁, ..., f_n). Траектории системы (5) называются характеристиками уравнения (3).

В линейном случае, как уже отмечалось, характеристики являются линиями уровня интегральных поверхностей. В квазилинейном случае дело обстоит несколько иначе. А именно, интегральные поверхности квазилинейного уравнения в некотором смысле целиком "склеены" из характеристик. Точнее, это утверждение выглядит так: через каждую точку интегральной поверхности проходит целиком лежащая в ней характеристика (см. рис. 2). Действительно, Пусть S = {(x, u(x)): x ∈ D} — интегральная поверхность уравнения (3), (x₀, u₀) ∈ S. Пусть φ(t) — решение задачи Коши

x′ = f[x, u(x)],

x(t0) = x0.

Рис. 2.

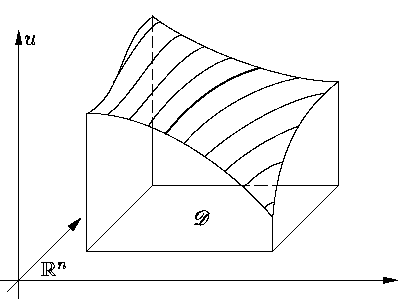
Тогда кривая (φ(t), ψ(t)), где ψ(t) = u[φ(t)], очевидно, лежит в S и, кроме того, является характеристикой.

Задача О9.1. Докажите.

Связь между уравнениями (3) и (4) выявляет следующее утверждение: если v = ψ(x, u) — решение уравнения (4) такое, что ∂ψ(x, u)/∂u ≠ 0, а функция u = φ(u) в некоторой области D ⊂ Rⁿ удовлетворяет уравнению

ψ[x, u(x)] = 0,

(6)

то в D функция φ является решением уравнения (3). Действительно, по теореме о дифференцировании неявной функции из (6) вытекает, что

∂φ(x) ∂xi = – ∂ψ(x, u) ∂xi | u = φ(x) · [ ∂ψ(x, u) ∂u | u = φ(x) ] –1 .

Подставляя u = φ(x) и вычисленное значение ∂φ(x)/∂x_i в левую часть уравнения (3) и учитывая, что функция ψ является решением уравнения (4), получим

f1[x, φ(x)] ∂φ(x) ∂x1  + ... + fn[x, φ(x)] ∂φ(x) ∂xn  =

– [ f1[x, φ(x)] ∂ψ(x, u) ∂x1 | u = φ(x)  + ... + fn[x, φ(x)] ∂ψ(x, u) ∂xn | u = φ(x) ]  ×

×  [ ∂ψ(x, u) ∂u | u = φ(x) ] –1  =

= fn+1[x, φ(x)] ∂ψ(x, u) ∂u | u = φ(x) · [ ∂ψ(x, u) ∂u | u = φ(x) ] –1  = fn+1[x, φ(x)].

Последнее и означает, что φ является в D решением уравнения (3).

На самом деле имеет место и обратное утверждение: если u = φ(x) — решение уравнения (3) в D, то найдется такое решение v = ψ(x, u) уравнения (4), что ∂ψ(x, u)/∂u ≠ 0 и ψ[x, φ(x)] = 0. Доказательство этого факта опускается в связи с его громоздкостью.

Описанная связь между уравнениями (3) и (4) позволяет строить общее решение уравнения (3). А именно, как уже говорилось, общее решение уравнения (4) имеет вид

v = F[V(x, u)],

где V — n-мерный невырожденный автономный первый интеграл системы (5), а F — произвольная непрерывно дифференцируемая скалярная функция. После этого общее решение u уравнения (3) находится из уравнения

F[V(x, u)] = 0.

Как и в случае обыкновенных дифференциальных уравнений, для уравнений в частных производных индивидуальное решение во множестве всех решений можно выделять различными способами. В данном очерке мы, не углубляясь в точные формулировки, дадим лишь геометрические представления о постановке задач Коши для уравнений (1) и (3). Задача Коши, или начальная задача для этих уравнений обычно ставится так. В пространстве Rⁿ задается (n – 1)-мерное многообразие (поверхность) Γ, например, как множество точек, выделяемых уравнением γ(x₁, ..., x_n) = 0, где γ — достаточно гладкая функция. На поверхности Γ задается функция u₀ и требуется найти решение (1) или (3) в окрестности многообразия Γ, совпадающее с u₀ на Γ.

Для уравнения (1) геометрическая интерпретация задачи Коши такова: через каждую точку (x, u₀(x)) графика функции u₀ требуется провести кривую на высоте u₀(x), проходящую над характеристикой уравнения (1), выпущенной из точки x (см. рис. 3а). Из эти кривых и "склеивается" интегральная поверхность, отвечающая решению задачи Коши.

Рис. 3.

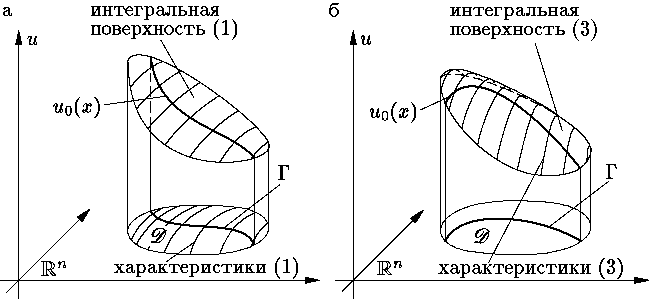
Для уравнения же (3) через каждую точку графика функции u₀ надо провести характеристику уравнения (3) и "склеить" из них интегральную поверхность, отвечающую решению задачи Коши (см. рис. 3б).

Следует подчеркнуть следующее обстоятельство. Если пересечение поверхности Γ с каждой характеристикой уравнения (1) состоит не более, чем из одной точки (например, в окрестности Γ это бывает так, если характеристики пересекают Γ трансверсально, т. е. под ненулевым углом), то задача Коши для этого уравнения в общей ситуации локально (т. е. в окрестности Γ) однозначно разрешима. Решение в этом случае строится так. Через точку x ∈ D надо провести характеристику уравнения (1) до ее пересечения с поверхностью Γ скажем в точке y. После этого надо положить u(x) = u₀(y) (см. рис. 4а).

Рис. 4.

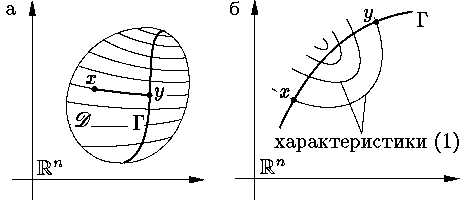
В противном случае задача Коши может и не иметь решения. На рис. 4б изображены характеристики уравнения (1). В этой ситуации значение решения в точке x должно, с одной стороны, равняться u₀(y), а с другой стороны, — u₀(x). Если u₀(x) ≠ u₀(y), то такая задача Коши решений не имеет.

Аналогичная (несколько более сложная) ситуация имеет место и для задачи Коши для уравнения (3)

Задача О9.2. Найдите решение задачи Коши

x1 ∂u ∂x1  + x2 ∂u ∂x2 = 0,

u(x1, x2)|Γ = sin x2,

где Γ = {(x₁, x₂): x₁ = 2}.

Литературные указания. Теория дифференциальных уравнений в частных производных первого порядка традиционно излагается в учебниках по теории обыкновенных дифференциальных уравнений: [Арнольд, Бибиков, Картан, Карташов — Рождественский, Петровский, Понтрягин, Тихонов — Васильева — Свешников, Федорюк, Хартман] и др.

Задачи. О9.3. Найдите общее решение уравнения

x1 ∂u ∂x1  + x2 ∂u ∂x2  + x3 ∂u ∂x3  = 0.

О9.4. Найдите общее решение уравнения

x1u ∂u ∂x1  + x2u ∂u ∂x2  = –x1x2.

О9.5. Докажите, что решение задачи Коши

x2 ∂u ∂x1 – x1 ∂u ∂x2 = 0,

u(x1, x2)|Γ = x1,

где Γ = {(x₁, x₂): x₁ = x₂,  1 < x₁ < x₂} в кольце R = {(x₁, x₂): √2 < x₁² + x₂² < 2√2} имеет единственное решение (найдите его), а в любой области, для которой R является ее собственным подмножеством, — континуум решений.

О9.6. Докажите, что задача Коши

x1 ∂u ∂x1 + x2 ∂u ∂x2 = 0,

u(x1, x2)|Γ = x2,

где Γ = {(x₁, x₂): x₂ = (x₁ – 1)²} не имеет решения ни в одной области, содержащей точку (1, 0).

О9.7. Докажите, что задача Коши

x1 ∂u ∂x1 – (x1+x2) ∂u ∂x2 = 0.

u(x1, x2)|Γ = φ(x1),

где Γ = {(x₁, x₂): x₂ = 0, x₁ ∈ R} имеет единственное решение в R² в том и только том случае, когда функция φ: R → R непрерывно дифференцируема и четна.

О9.8. Найдите общее решение u(t, x) уравнения

∂u ∂t + (a1, x) ∂u ∂x1 + ... + (an, x) ∂u ∂xn = 0

(a₁, ..., a_n — заданные n-мерные векторы, (·,·) — скалярное произведение в Rⁿ).

О9.9. Найдите решение уравнения из предыдущей задачи, удовлетворяющее условию u(0, x) = ||x||².

О9.10. Пусть C — объединение точек всех характеристик уравнения (1). Докажите, что если D — односвязная область в C, то любое решение (1) можно продолжить на всю область. Приведите пример неодносвязной области, на которую нельзя продолжить некоторое решение.

File based on translation from T_EX by T_TH, version 2.32.
Created 17 Jan 2000, 23:06.
Last modified 24 Apr 2002.