§ О17. Динамические системы — сложное поведение

В этом очерке мы опишем пример одной динамической системы, привлекающей последние тридцать лет большое внимание исследователей. Эта трехмерная динамическая система была введена в научный обиход в 1963 году Э. Лоренцем, занимавшемся моделированием атмосферных процессов. С тех пор она вызывала и продолжает вызывать огромное число исследований и публикаций. Основной причиной, породившей такой интерес к системе уравнения Лоренца, является хаотическое поведение ее траекторий. Ясности в исследуемых вопросах еще нет. Некоторые результаты обоснованы только на "физическом уровне строгости'' или численно и говорит о сформировавшейся теории рано. Поэтому изучение рекомендуемой литературы требует довольно высокой математической подготовки. По этой же причине этот очерк не сопровождается задачами.

Система уравнений Лоренца — это трехмерная система нелинейных автономных дифференциальных уравнений первого порядка вида

x'1= –σx1 + σx2, x'2= –x1x3 + rx1 – x2, x'3= x1x2 – bx3.

(1)

В ней σ, b и r — параметры. Эта система возникла в задаче о моделировании конвективного течения жидкости, подогреваемой снизу. Такое течение описывается системой дифференциальных уравнений в частных производных. Система (1) получается из нее проектированием на специальное трехмерное подпространство.

В результате численного интегрирования системы (1) Э. Лоренц обнаружил, что при σ = 10, b = 8/3 и r = 28 у этой динамической системы, с одной стороны, наблюдается хаотическое, нерегулярное поведение всех траекторий (см. рис. 1, на котором изображена зависимость координаты x₂ одной из траекторий от времени), а, с другой стороны, все траектории притягиваются при t → +∞ к некоторому сложно устроенному множеству — аттрактору (от англ. to attract — притягивать, привлекать).

Рис. 1.

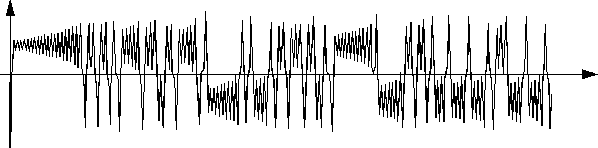
Такое поведение решений ассоциируется с так называемыми турбулентными (беспорядочными, хаотическими) течениями жидкости. Это породило надежды на продвижение в одной из важнейших проблем современной гидро- и аэродинамики — проблеме описания турбулентности. В частности, этим объясняется бурный интерес ученых к этой системе. К настоящему времени ответ на вопрос: имеет ли отношение к турбулентности система Лоренца и ее аналоги не известен. Хотя здесь есть масса доводов как pro, так и contra.

Мы попытаемся описать имеющиеся представления о появлении и структуре аттрактора в системе Лоренца. Зафиксируем в (1) σ = 10, b = 8/3 и будем увеличивать r, начиная с нуля.

Рис. 2.

При r < 1 система Лоренца имеет асимптотически устойчивую в целом стационарную точку — начало координат. К ней притягиваются все траектории (см. рис. 2). Здесь же отметим, что начальная стадия нашего анализа (вплоть до рис. 4) элементарна и читатель может проделать ее сам. Когда r переваливает через единицу, происходит первая бифуркация. Начало координат теряет устойчивость и от него отделяются две новые устойчивые стационарные точки

X1 = (√b(r – 1), √b(r – 1), r – 1)

и

X2 = (–√b(r – 1), –√b(r – 1), r – 1)

Рис. 3.

У линеаризованной в нулевой стационарной точке системы два отрицательных и одно положительное собственное значение. В соответствии с этим у нулевой стационарной точки есть двумерный входящий ус и одномерный выходящий (см. рис. 3). У линеаризованных в точках X₁ и X₂ систем все собственные значения отрицательны.

При возрастании параметра r пара отрицательных собственных значений этих систем превращается в пару комплексно сопряженных собственных значений. Это, в частности, соответствует тому, что выходящие усы G₁ и G₂ нулевой стационарной точки начинают закручиваться как спирали около стационарных точек X₁ и X₂, соответственно (см. рис. 4).

Рис. 4.

Рис. 5.

С дальнейшим ростом r стационарные точки X₁ и X₂ поднимаются выше (они лежат в плоскости x₃ = r – 1), а спиралевидные траектории "разбухают". Это происходит до тех пор, пока при r ≈ 13.92 (это значение можно найти только численно) спирали, начинающиеся как выходящие усы нуля, попадают на его входящий ус, образуя две гомоклинические траектории Γ₁ и Γ₂ (см. рис. 5).

При возрастании r в этот момент происходит бифуркация гомоклинических траекторий с образованием двух неустойчивых циклов Φ₁ и Φ₂ (см. рис. 6). Линейные части операторов последования, отвечающих этим циклам, имеют по одному мультипликатору большему единицы и по одному — меньшему единицы, и следовательно, по одному направлению траектории к этим циклам притягиваются, а по другому — отталкиваются. Выходящие усы G₁ и G₂ нулевой стационарной точки теперь уже не попадают на ее входящий ус (см. рис. 6) — они попадают в области притяжения стационарных точек X₂ и X₁, соответственно (а не X₁ и X₂, как было раньше) и закручиваются около них.

Рис. 6.

При r ≈ 24.06 происходит очередная бифуркация и G₁ и G₂ попадают на притягивающие многообразия (неустойчивых) циклов Φ₂ и Φ₁ (см. рис. 7). Следующая бифуркация происходит при r = r₀ = σ(σ + b + 3)/(σ – b – 1) ≈ 24.74. В этот момент у линеаризованных в точках X₁ и X₂ систем появляется пара собственных значений на мнимой оси (при r > r₀ эти собственные значения имеют положительные вещественные части). Стационарные точки X₁ и X₂ поглощают неустойчивые циклы Φ₁ и Φ₂, теряя устойчивость (бифуркация Пуанкаре — Андронова — Хопфа). Система жестко возбуждается.

Рис. 7.

Во время описанного процесса, начиная с r = 13.92 у системы Лоренца появляется предельное инвариантное множество, но до r = r₀ оно не является устойчивым, т. е. не притягивает к себе траектории. При r ∈ (r₀,50] это множество Λ становится "устойчивым". Это и есть собственно аттрактор Лоренца. Представление о том как он выглядит может дать рис. 8, на котором изображена одна траектория системы Лоренца при r = 28: при t→ +∞ она стремится к аттрактору. Траектория делает по несколько оборотов то вокруг неустойчивой стационарной точки X₁, то вокруг неустойчивой стационарной точки X₂, меняя их "случайным образом" (см. рис. 1).

Рис. 8.

Известно, что аттрактор Лоренца обладает следующими свойствами (обоснование этих свойств к настоящему моменту содержит эмпирические этапы, основанные на результатах численных расчетов).

Во-первых, Λ является аттрактором в том смысле, что существует открытое в R³ множество A такое, что Λ = ∩_t≥0 g^tA (здесь g^t — оператор сдвига по траекториям системы Лоренца). Другими словами, все траектории, начинающиеся в A (в данном случае в качестве A можно взять все R³, исключая начало координат), притягиваются к Λ.

Во-вторых, в Λ имеется всюду плотное множество периодических траекторий, причем каждая из них неустойчива.

В-третьих, траектории, лежащие в Λ, экспоненциально разбегаются и поэтому при сколь угодно малом возмущении начальных данных в задаче Коши для системы Лоренца решения на большом интервале времени могут различаться очень сильно. Это делает описываемый системой Лоренца процесс в некотором смысле недетерминированным.

В-четвертых, известно, что локально аттрактор Лоренца устроен как произведение канторова совершенного множества на отрезок.

Аттракторы, обладающие перечисленными свойствами, обнаружены сейчас во многих динамических системах. Их обычно называют странными аттракторами.

С тем, что происходит в системе Лоренца при больших r ясности пока нет. В некоторых интервалах изменения параметра обнаружены устойчивые периодические решения. Интересное явление наблюдается при r ∈ [210, 234] и r ∈ [145, 149]. При r = 234 система Лоренца имеет устойчивый цикл, который при уменьшении rиспытывает бифуркацию удвоения периода, теряя устойчивость и порождая устойчивый цикл двойного периода. При дальнейшем уменьшении r новый цикл также теряет устойчивость и от него, в свою очередь, ответвляется цикл двойного периода и т. д. Таким образом, возникает бесконечная последовательность {r_k} значений параметра, при котором система Лоренца испытывает бифуркацию удвоения периода. Эта последовательность удовлетворяет недавно открытому закону универсальности Фейгенбаума:

lim k→∞ rk – rk–1 rk+1 – rk = δ,

где δ = 4.6692... — универсальная постоянная, которая, по современным представлениям, по-видимому, не зависит от конкретной динамической системы, испытывающей бесконечную последовательность бифуркаций удвоения периода.

Литературные указания. Данный раздел теории обыкновенных дифференциальных уравнений новый и бурно развивающийся. Результаты описаны, в основном, в статьях и монографиях. (По этой же причине отсутствуют задачи в конце очерка.) Учебной литературы пока нет. Мы можем порекомендовать для начального изучения [Марсден — Мак-Кракен, Неймарк — Ланда, Странные аттракторы].

Апплет на рис. 9 позволяет просматривать поведение некоторых динамических систем с хаотическим поведением, самостоятельно задавая значения параметров.

Рис. 9.

File based on translation from T_EX by T_TH, version 2.32.
Created 30 Dec 1999, 14:03.
Last modified 27 Apr 2002.