§ 4.3. Устойчивость линейных систем

В этом параграфе изучаются критерии устойчивости, асимптотической и экспоненциальной устойчивости для линейных систем с переменными и постоянными коэффициентами.

4.3.1. Приведенная система для (ЛС). Для линейной системы

x′ = A(t)x + b(t),

(ЛС)

aij, bi ∈ C([t0, +∞), R),

и любого ее решения x = φ(t) приведенная система совпадает с соответствующей (ЛОС).

Д о к а з а т е л ь с т в о.  Произведем замену y = x – φ(t):

y′ = A(t)x + b(t) – A(t)φ(t) – b(t) = A(t)(x – φ(t)) = A(t)y.

4.3.2. Замечание о терминологии. Из предыдущего пункта следует, что решения (ЛС) могут обладать или не обладать каким-то свойством устойчивости только все одновременно, и при этом соответствующее свойство обязательно имеется или не имеется у нулевого решения (ЛОС) (и всех других ее решений).

Поэтому употребляют термины устойчивая линейная система, асимптотически устойчивая линейная система и т. д.

4.3.3. Критерии устойчивости (ЛС). Пусть Φt0(t) — фундаментальная матрица (ЛОС), нормальная в t0. Утверждается, что

(а) (ЛС) устойчива ⇔ Φt0(t) ограничена на [t0, +∞);

(б) (ЛС) асимптотически устойчива ⇔ Φt0(t) → 0 при t → +∞ ⇔ (ЛС) асимптотически устойчива в целом;

(в) (ЛС) экспоненциально устойчива ⇔ (M > 0, γ > 0) ∀ (t ≥ t0) [||Φt0(t)|| ≤ Me–γ(t–t0)] ⇔ (ЛС) экспоненциально устойчива в целом.

Д о к а з а т е л ь с т в о.  (а) Пусть (ЛС) устойчива, т. е. устойчиво нулевое решение (ЛОС). Положив в определении устойчивости ε = 1, найдем δ > 0 такое, что

||x0|| < δ ⇒ ||gt0t(x0)||= ||Φt0(t)x0|| < 1    (t ≥ t0).

Следовательно, если ||x|| = 1, то ||δx/2|| < δ и

||Φt0(t)x0|| = 2 δ ||Φt0(t)(δx/2)|| < 2 δ .

Поэтому ||Φt0(t)|| < 2/δ, т. е. Φt0(t) ограничена.

Если, наоборот, известно, что

||Φt0(t)|| ≤ H   (t ≥ t0),

то

||gt0t(x0)||≤ H||x0||,

так что для любого ε > 0 в определении устойчивости нулевого решения (ЛОС) можно взять δ = ε/H.

(б) Пусть (ЛС) асимптотически устойчива. Тогда

||x0|| < Δ ⇒ ||Φt0(t)x0|| → 0 при t → +∞.

В частности для орта e_k

||Φt0(t)ek|| = 2||ek|| Δ · || Φt0(t) ( ek· Δ 2||ek|| ) || → 0 при t → +∞

(мы рассматриваем произвольную норму в Rn, поэтому, возможно, ||ek|| ≠ 1). Это означает, что все столбцы матрицы Φt0(t) стремятся к нулю при t → +∞; но тогда и сама матрица стремится к нулю.

Пусть дано, что Φt0(t) → 0 при t → +∞. Тогда для любого x0 ∈ Rn

gt0t(x0)= Φt0(t)x0 → 0 при t → +∞,

т. е. (ЛС) асимптотически устойчива в целом.

Наконец, из асимптотической устойчивости в целом следует асимптотическая устойчивость.

(в) Если (ЛС) экспоненциально устойчива, то существуют Δ₁ > 0, M > 0 и γ > 0 такие, что

||x0|| < Δ1 ⇒ ||Φt0(t)x0|| ≤ Me–γ(t–t0)||x0||    (t ≥ t0).

Поэтому для любого x, удовлетворяющего условию ||x|| = 1, будем иметь:

||Φt0(t)x|| = 2 Δ1 || Φt0(t) ( x· Δ1 2 ) || ≤

≤ 2 Δ1 Me–γ(t–t0) || x0· Δ1 2 || = Me–γ(t–t0)||x||.

Следовательно,

||Φt0(t)|| ≤ Me–γ(t–t0)    (t ≥ t0).

Наоборот, если выполнено последнее неравенство, то для любого x₀

||Φt0(t)x0|| ≤ ||Φt0(t)||·||x0|| ≤ Me–γ(t–t0)||x0||   (t ≥ t0),

т. е. (ЛС) экспоненциально устойчива в целом.

Остается заметить, что экспоненциальная устойчивость в целом влечет экспоненциальную устойчивость.

4.3.4. Оценки нормы e^At. Переходя к рассмотрению линейных систем с постоянными коэффициентами

x′ = Ax + b(t),

(ЛСПК)

x′ = Ax,

(ЛАОС)

введем следующие обозначения: α — максимальная вещественная часть собственных значений A, k — максимальная размерность жордановых клеток A, отвечающих собственным значениям с вещественной частью α.

Утверждается, что

(а) ∃ (m > 0, M > 0) ∀ (t ≥ t0) [meαt tk–1 ≤ ||eAt|| ≤ Meαt(t + 1)k–1 ];

(1)

(б) ∃ (H: (0, +∞) → (0, +∞)) ∀ (ε > 0, t ≥ 0) [||eAt|| ≤ H(ε)e(`α+ε)t].

Д о к а з а т е л ь с т в о.  (а) Из равенства

eAt = PeJtP–1

(см. п. 3.3.4) вытекает существование таких m₁ > 0, M₁ > 0, что

m1||eJt|| ≤ ||eAt|| ≤ M1||eJt||.

(2)

В силу эквивалентности всех норм в пространстве матриц существуют такие положительные m₂ и M₂, что

m2· max  i, j |(eJt)ij| ≤ ||eJt|| ≤ M2· max  i, j |(eJt)ij|.

(3)

Принимая во внимание описанный в п. 3.3.5 вид элементов матрицы e^Jt и равенство |e^λt| = e^Re λt, получим для t ≥ 0:

1 (k – 1)! ·eαttk–1 ≤ max i, j |(eJt)ij|.

Отсюда и из нижних оценок в (2), (3) вытекает первое из неравенств (1).

Далее, если

(eJt)ij = eλt tk–1 (k – 1)!

то дробь

|(eJt)ij| eαt(t + 1)k–1 = 1 (k – 1)! e(Re λ–α)t tk–1 (t + 1)k–1

ограничена на [0, +∞). При Re λ < α это следует из того, что она непрерывна на [0, +∞) и стремится к нулю при t → +∞, а при Re λ = α — из неравенства k ≤ k. Итак, при t ≥ 0

max i, j |(eJt)ij| ≤ M3eαt(t + 1)k–1 .

Отсюда и из (2), (3) вытекает верхняя оценка в (1).

(б) Наконец, заметим, что при ε > 0

eαt(t + 1)k–1 = e(`α+ε)t· [e–εt(t + 1)k–1 ]≤ M4(ε) e(`α+ε)t,

так как выражение в квадратных скобках непрерывно и стремится к нулю при t → +∞. Поэтому (б) следует из (а).

4.3.5. Критерии устойчивости (ЛСПК).

Утверждается, что

(а) (ЛСПК) устойчива ⇔ [(α < 0) или (α = 0 и k = 1)];

(б) (ЛСПК) асимптотически устойчива ⇔ α < 0 ⇔ (ЛСПК) экспоненциально устойчива в целом.

Д о к а з а т е л ь с т в о.  (а) Из устойчивости (ЛСПК) по критерию устойчивости (ЛС) следует ограниченность eAt на [t0, +∞) и, следовательно, на [0, +∞). Воспользовавшись нижней оценкой ||eAt|| из предыдущего пункта, получим, что при t ≥ 0 ограничена функция eαttk–1 . Но последнее возможно лишь при α ≤ 0, причем, если α = 0, то должно быть k = 1.

Обратная импликация, очевидно, вытекает из верхней оценки в (1).

(б) Если (ЛСПК) асимптотически устойчива, то по критерию устойчивости (ЛС) e^At → 0 при t → +∞. Воспользовавшись нижней оценкой ||e^At|| в (1), получаем, очевидно, что α < 0.

Если же известно, что α < 0, то мы можем выбрать ε > 0 так, что

α + ε = –γ < 0.

Тогда из верхней оценки (б) предыдущего пункта следует неравенство

||eAt|| ≤ Me–γt    (t ≥ 0),

которое в силу критерия экспоненциальной устойчивости (ЛС) означает, что (ЛСПК) экспоненциально устойчива в целом.

Завершает доказательство очевидное замечание, что из экспоненциальной устойчивости в целом следует асимптотическая устойчивость.

4.3.6. Критерий Гурвица. Рассматривается многочлен

h(λ) = anλn + an–1λn–1 + ... + a1λ +

(4)

с вещественными коэффициентами и предполагается, что

a0 > 0, an ≠ 0.

(5)

Утверждается: для того, чтобы все корни многочлена (4) имели отрицательные вещественные части, необходимо и достаточно, чтобы были положительны все главные диагональные миноры следующей матрицы Гурвица:

Γ = (Γij)ni,j = 1,    Γij = { a2i – j если 0 ≤ 2i – j ≤ n, 0 в противном случае.

Доказательство критерия Гурвица, а также формулируемого ниже критерия Михайлова, выходят за рамки нашей книги.

П р и м е р.  Рассмотрим характеристические многочлены для уравнения маятника, линеаризованного в нижнем и верхнем положении равновесия:

ψ′′ + rψ′ + ω2ψ = 0;  ψ′′ + rψ′ – ω2ψ = 0,

т. е. многочлены

h1(λ) = λ2 + rλ + ω2;  h2(λ) = λ2 + rλ – ω2;

(6)

Соответствующие им матрицы Гурвица таковы:

Γ1 = (  r ω2 0 1 ) ;   Γ2 = (  –r ω2 0 –1 ) .

Для формирования матрицы Γ₂ пришлось во втором из уравнений (6) изменить знаки всех коэффициентов, иначе не было бы выполнено первое из условий (5). Очевидно, условие Гурвица положительности главных диагональных миноров выполнено для Γ₁ и не выполнено для Γ₂. Поэтому линеаризованная система асимптотически устойчива для нижнего положения равновесия и не является таковой для верхнего.

Отметим еще полезное необходимое, но не достаточное условие гурвицевости (т. е. отрицательности всех вещественных частей всех корней) многочлена (4), удовлетворяющего условиям (5): все коэффициенты a_k должны быть положительны.

Для второго из уравнений (6), умноженного на –1, это условие не выполнено, поэтому матрицу Γ₂ можно было не составлять. Для многочлена второй степени, удовлетворяющего требованиям (5), сформулированное условие не только необходимо, но и достаточно (докажите).

4.3.7. Критерий Михайлова. Для многочлена (6) построим годограф Михайлова, т. е. ориентированную кривую, описываемую в комплексной плоскости точкой

z = h(iω),

когда вещественное число ω изменяется от 0 до +∞. Допустим, что годограф Михайлова не проходит через начало координат, т. е. многочлен h не имеет число мнимых корней. Утверждается: для гурвицевости многочлена h необходимо и достаточно, чтобы его годограф Михайлова делал поворот вокруг начала координат против часовой стрелки на угол nπ/2, где n — степень полинома.

П р и м е р.  Построим годограф Михайлова для первого многочлена из (6) h₁(λ) = λ² + rλ + ω² (здесь мы немного изменили обозначение):

h1(iω) = –ω2 + rωi + ω2 = (ω2 – ω2) + rωi.

Рис. 1.

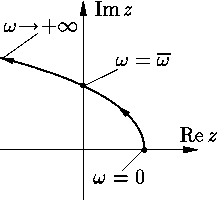
Эта кривая изображена на рис. 1. Угол φ = arg h₁(iω) при ω → +∞ стремится к π, т. к. tg φ = rω/(ω² – ω²) → 0. Итак, годограф делает поворот вокруг начала координат против часовой стрелки на угол 2π/2, т. е. многочлен гурвицев. Для второго из многочленов (6) угол поворота годографа Михайлова будет равен 0 (проверьте).

4.3.8. Контрольные вопросы

4.3.8.1. Докажите, что все решения устойчивой линейной неоднородной системы ограничены или неограничены одновременно.

4.3.8.2. Покажите, что что если система x′ = Ax асимптотически устойчива, то система x′ = –Ax неустойчива.

4.3.8.3. Докажите, что если система x′ = Ax устойчива, то система x′ = Ax – x асимптотически устойчива.

4.3.8.4. Покажите, что если скалярное уравнение

x′ = a(t)x

(7)

устойчиво и a₁(t) ≤ a(t) при всех t, то уравнение x′ = a₁(t)x также устойчиво.

4.3.8.5. Докажите, что если a > 0 и ∫ 0+∞|b(s)|ds < ∞ (b: R → R — непрерывная функция), то все решения скалярного уравнения x′′ + [a + b(t)]x = 0 ограничены на [0, +∞).

4.3.8.6. Докажите, что если на диагонали треугольной матрицы A стоят различные неположительные числа, то соответствующая (ЛАОС) устойчива.

4.3.8.7. С помощью критерия Гурвица исследуйте устойчивость уравнения x′′′ + x′′ + x′ + 2x = 0.

4.3.8.8. С помощью критерия Михайлова исследуйте устойчивость уравнения x′′′ + 2x′′ + 2x′ + 3x = 0.

4.3.9. Задачи

Ниже предполагается, что в уравнении (7) функция a: R → R непрерывна.

4.3.9.1. Найдите какие-нибудь необходимые и достаточные условия, которым должна удовлетворять функция a(t), чтобы скалярное уравнение (7) было устойчивым (асимптотически устойчивым).

4.3.9.2. Докажите, что нулевое решение уравнения (7) асимптотически устойчиво, если

lim  t→+∞

a(t) < 0 и неустойчиво, если

lim  t→+∞

a(t) > 0.

4.3.9.3. Приведите пример уравнения (7), в котором a(t) < 0 при всех t, а нулевое решение не является асимптотически устойчивым.

4.3.9.4. Докажите, что уравнение (7) неустойчиво, если a(t) строго положительна и периодична.

4.3.9.5. Докажите, что уравнение (7) асимптотически устойчиво, если a(t) — строго отрицательная периодическая функция.

4.3.9.6. Пусть все собственные значения матрицы A имеют отрицательную вещественную часть, а непрерывная матрица-функция B(t) такова, что ∫ 0+∞||B(s)||ds < ∞. Докажите, что система x′ = [A + B(t)]x устойчива. Если же B(t) → 0 при t → +∞, то она асимптотически устойчива.

4.3.9.7. Пусть в (ЛОС) непрерывная матрица A(t) удовлетворяет условию Лаппо — Данилевского (см. задачу 3.3.8.13) и существует предел

A0 = lim t → +∞ 1 t ∫ t 0 A(s) ds.

Докажите, что если все собственные значения матрицы A₀ имеют отрицательную вещественную часть, то (ЛОС) асимптотически устойчива.

4.3.9.8. Докажите, что оператор g^t_t0 сдвига по траекториям (ЛОС) удовлетворяет оценке

exp ( – ∫ t t0 ||A(s)|| ds ) ≤ ||gt0t||≤ exp ( ∫ t t0 ||A(s)|| ds )    (t ≥t0).

4.3.9.9. На плоскости параметров (α, β) ∈ R² найдите максимальное множество тех (α, β), при которых

x′1 = –x1 + αx2 + βx3, x′2 = –αx1 – x2 + αx3, x′3 = –βx1 – αx2 – x3

устойчива (это множество параметров называется областью устойчивости системы).

4.3.9.10. Покажите, что если какое-нибудь ненулевое решение (ЛАОС) ограничено на (–∞, 0], то система не является асимптотически устойчивой.

File based on translation from T_EX by T_TH, version 2.32.
Created 20 Jan 2002, 16:00.
Last modified 19 Apr 2002.