§ 1.2. Уравнения с разделяющимися переменными

Лишь немногие обыкновенные дифференциальные уравнения допускают интегрирование в квадратурах т. е. выражение общего решения или полного интеграла через известные функции и интегралы от них. Среди интегрируемых типов обыкновенных дифференциальных уравнений важную роль играют уравнения с разделяющимися переменными, которые рассматриваются в настоящем параграфе.

1.2.1. О дифференциалах. Напомним определения и основные факты из курса математического анализа, относящиеся к понятию дифференциала функции.

а) Дифференциалом дифференцируемой функции x = φ(t) называется выражение

dx = φ′(t)dt

с двумя независимыми переменными t ∈ D(φ) и dt ∈ R.

б) Дифференциалом дифференцируемой функции двух переменных y = Φ(t, x) называется выражение

dy = ∂Φ ∂t dt + ∂Φ ∂x dx

с независимыми переменными t, x, dt и dx.

в) Имеет место инвариантность формы первого дифференциала : если функции y = Φ(t, x), t = ψ(s), x = φ(s) дифференцируемы, то

d[Φ(t, x)|t = ψ(s), x = φ(s)] = d[Φ(t, x)]|t = ψ(s), dt = ψ′ds, x = φ(s), dx = φ′ds),

т. е. операции подстановки и вычисления первого дифференциала перестановочны. В левой части дифференциал вычисляется по s, в правой — по x, y; во втором случае получается выражение с четырьмя независимыми переменными, вместо которых затем подставляются указанные выражения.

г) Если dφ(t) ≡ 0 и D(φ) — промежуток, то найдется такая константа C, что φ(t) ≡ C.

1.2.2. О записи обыкновенных дифференциальных уравнений в дифференциалах. Уравнение вида

f(t, x)x′ = g(t, x)

(1)

часто записывают "в дифференциалах":

f(t, x)dx = g(t,x)dt.

(2)

Такая запись получается из (1) умножением на дифференциал независимой переменной dt, причем под решением уравнения (2) понимается определенная на промежутке функция x = φ(t), для которой справедливо тождество

f[t, φ(t)]φ′(t)dt = g[t, φ(t)]dt    (t ∈ D(φ), dt ∈ R).

(2а)

При таком понимании (1) ⇔ (2). Действительно, из тождества

f[t, φ(t)]φ′(t) = g[t, φ(t)]    (t ∈ D(φ)).

(2б)

очевидно следует (2a), а из (2a) при dt = 1 получается (2б).

Оказывается, если переменные в уравнении (2) "разделены", т. е. f не зависит от t, а g не зависит от x, то уравнение интегрируется.

1.2.3. Утверждение об уравнении с разделенными переменными. Пусть в уравнении

f(x)dx = g(t)dt,

(3)

функции f и g на своих областях определения имеют первообразные F и G:

F′(x) = f(x)   (x ∈ D(f)),    G′(t) = g(t)   (t ∈ D(g)).

(4)

Тогда уравнение (3) эквивалентно уравнению

F(x) = G(t) + C   (x ∈ D1).

(5)

Другими словами, (5) есть полный интеграл уравнения (3).

Д о к а з а т е л ь с т в о.  Пусть область определения D(φ) функции x = φ(t) есть промежуток и φ есть решение уравнения (3). Это означает, что

[f(x)dx – g(t)dt]|x = φ(t), dx = φ′dt = 0    (t ∈ D(φ), dt ∈ R).

В силу условий (4) последнее равенство эквивалентно тождеству

d[F(x) – G(t)]|x = φ(t), dx = φ′dt)] ≡ 0   (t ∈ D(φ), dt ∈ R),

которое в силу инвариантности формы первого дифференциала, в свою очередь, эквивалентно соотношению

d[F(φ(t)) – G(t)] = 0    (t ∈ D(φ), φ ∈ D1).

Наконец, последнее, очевидно эквивалентно тождеству

F[φ(t)] = G(t) + C   (t ∈ D(φ), φ ∈ D1),

означающему, что φ — решение (5).

1.2.4. Линейное однородное уравнение. В качестве примера проведем решение линейного однородного уравнения

x′ = a(t)x,

(6)

которое играет в теории обыкновенных дифференциальных уравнений важную самостоятельную роль. Переменные в уравнении не разделены, но легко разделяются: в области, где

x ≠ 0,

(7)

его можно записать в виде

dx x = a(t)dt

(8)

Будем считать, что

функция a: J ⊂ R → R непрерывна (J — промежуток).

(9)

Тогда (8) в силу утверждения об уравнении с разделенными переменными эквивалентно уравнению

∫ 0 dx x = ∫ 0 a(t)dt + C,

(10)

где нули под интегралами обозначают выбор какой-нибудь одной из первообразных. Положим

∫ 0 dx x  = ln |x|,    ∫ 0 a(t)dt = ∫ t t0 a(s)ds,

где t₀ — любая фиксированная точка промежутка J. Уравнение (10) запишется в виде

ln |x| = ∫ t t0 a(s)ds + C,

или

|x| = C1exp ∫ t t0 a(s)ds    (C1 = eC > 0).

(11)

Решения уравнения (11) не принимают нулевых значений, т. е. каждое из них либо всюду положительно, либо всюду отрицательно. Следовательно, (11) эквивалентно уравнению

x = C2exp ∫ t t0 a(s)ds    (C2 ≠ 0).

(12)

Итак, (12) есть общее решение уравнения (8) и, следовательно, частичное решение уравнения (6).

В части (t, x)-плоскости, выделяемой равенством

x = 0,

(13)

уравнение (6), очевидно, эквивалентно (13). Наконец, уравнение (13), которое одновременно является своим общим решением, можно включить в (12):

x = C·exp ∫ t t0 a(s)ds    (C ∈ R).

(14)

Можно ли утверждать, что это общее решение уравнения (6)?

1.2.5. Замечание о ловле змей. Если поиск всех решений уравнения (6) представлять как ловлю змей в двух "смежных комнатах", одна из которых определяется неравенством (7), а другая — равенством (13), то можно сказать, что формула (14) вылавливает всех змей, целиком находящихся в первой комнате, и всех змей, целиком расположенных во второй. Однако она не учитывает тех змей, которые, возможно, частично лежат в первой комнате и частично — во второй. В следующем пункте мы покажем, что в данном случае таких змей нет — это будет означать, что формула (14) дает общее решение уравнения (6) при условии (9).

1.2.6. Утверждение о линейном однородном уравнении. При выполнении условия (9) формула (14) дает общее решение уравнения (6).

Д о к а з а т е л ь с т в о.  Из рассуждений п. 1.2.4 следует, что (14) ⇒ (6). Покажем, что (6) ⇒ (14). Пусть x = φ(t) — какое-нибудь решение уравнения (6) и Φt0(t) — конкретное его решение, определяемое формулой

Φt0(t) = exp ∫ t t0 a(s)ds.

Нам нужно показать, что φ удовлетворяет (14), т. е. при некотором выборе C

φ(t) ≡ CΦt0(t).

Поскольку Φt0(t) ≠ 0, это эквивалентно соотношению

φ(t) Φt0(t) ≡ C.

Последнее тождество действительно имеет место, так как производная от его левой части тождественно равна нулю (напомним, что φ и Φt0 — решения (6)):

d dt φ(t) Φt0(t)  =  φ′(t)Φt0(t) – φ(t)Φ′t0(t) Φ2t0(t)  =

=  a(t)φ(t)Φt0(t) – φ(t)a(t)Φt0(t) Φ2t0(t)  = 0.

1.2.7. Основные этапы решения обыкновенных дифференциальных уравнений. Перечислим характерные этапы, из которых состояло решение уравнения (6) и которые обычно присутствуют при решении ОДУ.

1) Разбиение области изменения переменных.

2) Разделение переменных.

3) Интегрирование уравнения с разделенными переменными.

4) "Арифметические" эквивалентные преобразования, включающие переобозначение произвольных постоянных.

5) Объединение общих решений, полученных в разных областях изменения переменных.

6) Исследование вопроса о существовании "составных" решений.

Последний этап часто опускают, считая основной задачей не поиск всех решений, а поиск функций, из которых можно составить любое решение.

В дальнейшем мы познакомимся еще с двумя важными приемами, применяемыми при решении ОДУ.

7) Интегрирование уравнений в полных дифференциалах.

8) Замена переменных.

1.2.8. Пример более сложной ловли змей. Мы приведем пример, показывающий, что простое объединение общих решений, полученных в разных областях изменения переменных может привести к потере решений. Рассмотрим уравнение

dx dt = 2√x

(15)

и разобьем область D(f) = R × [0, +∞), выделив подобласти условиями

x ≠ 0,

(16а)

x = 0.

(16б)

В первом случае (15) эквивалентно уравнению с разделенными переменными

dx 2√x = dt.

Интегрируя его, получаем

√x = t+C,

и, далее,

x = (t + C)2    (t > –C).

(17)

Система (15) ∧ (16б), очевидно, имеет общее решение (16б).

Рис. 1.

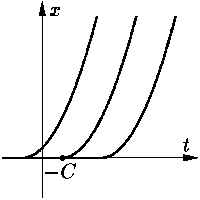
Однако, совокупность (17) ∨ (16б) не описывает всех решений исходного уравнения (15). Действительно, оно имеет еще по крайней мере семейство решений вида

x = { 0 при t ≤ –C, (t + C)2 при t > –C

(18)

(см. рис. 1).

Покажем, что других решений нет. Действительно, если решение φ не входит ни в (17), ни в (16б), то φ(t₁) = 0 и φ(t₂) > 0 при некоторых t₁ < t₂. Из (15) следует, что φ(t) ≥ 0 при всех t ∈ D(φ), т. е. φ не убывает. Поэтому найдется t₃ ∈ [t₁, t₂) такое, что φ(t) = 0 при t ≤ t₃ и φ(t) > 0 при t > t₃. Поскольку при x ≠ 0 (15) эквивалентно (17), получаем, что φ(t) = (t – t₃)² при t > t₃. Итак, φ есть решение вида (17), и утверждение доказано.

1.2.9. Контрольные вопросы

1.2.9.1. Как разделить переменные в уравнении txx′ + 1 = x?

1.2.9.2. Если x = φ₁(t) и x = φ₂(t) — решения уравнения (6), а λ₁, λ₂ ∈ R, то является ли функция x = λ₁φ₁(t) + λ₂φ₂(t) решением этого уравнения?

1.2.9.3. При каких условиях функции x ≡ 0 и x ≡ 1 являются решениями уравнения (6)?

1.2.9.4. Найдите общее решение уравнения

x′ = 2√|x|

1.2.10. Задачи

1.2.10.1. Найдите общее решение уравнения x′ = sin x.

1.2.10.2. Найдите общее решение уравнения x′ –  tx² = 2tx.

1.2.10.3. Найдите общее решение уравнения x′ –  e^t+x = 0.

1.2.10.4. Найдите ограниченное при t → +∞ решение уравнения 3x²x′ + 2t = 2tx³.

1.2.10.5. Покажите, что любое решение уравнения x′ = [(x² + 1)/(t⁴ + 1)]^1/3 имеет конечные пределы при t → ±∞.

1.2.10.6. Найдите общее решение уравнения x′ = 3x^2/3.

1.2.10.7. Покажите, что если sup{a(t): t ∈ R} < 0, то любое решение уравнения (6) стремится к нулю при t → +∞.

1.2.10.8. Докажите, что если в уравнении (6) функция a T-периодическая и имеет нулевое среднее за период: ∫T0a(s) ds = 0, то все решения ограничены.

File based on translation from T_EX by T_TH, version 2.32.
Created 1 Jan 2002, 13:03.
Last modified 8 Apr 2002.