§ 1.3. Уравнения в полных дифференциалах

В доказательстве утверждения об уравнении с разделенными переменными основную роль играло то, что выражение f(x)dx – g(t)dt есть дифференциал от функции двух переменных Φ(t, x) = F(x) – G(t). В этом параграфе мы реализуем эту идею в более общем виде. Предварительно будет изучена так называемая симметричная трактовка ОДУ, которая в ряде случаев оказывается более удобной, чем обычная.

1.3.1. Разные трактовки ОДУ. Уравнения вида

f(t, x)dx + g(t,x)dt = 0,

(1)

Φ(t, x) = C

допускают три разные трактовки:

обычную: x — неизвестная функция, t — аргумент;

обратную: t — неизвестная функция, x — аргумент;

симметричную: x и t — две неизвестные функции от некоторого аргумента, не входящего в уравнение, например, s.

Разумеется, эти трактовки между собой не эквивалентны, однако тесно связаны. Рассмотрим уравнения

F(t, x, dt, dx, C) = 0,

(2)

G(t, x, dt, dx,C) = 0

(3)

в обычной трактовке и будем обозначать через (2s), (3s) их симметричную трактовку.

1.3.2. Утверждение о симметричной трактовке. Если (2s) ⇒ (3s), то (2) ⇒(3).

Д о к а з а т е л ь с т в о.  Итак, пусть (2s) ⇒ (3s) и φ — решение уравнения (2). Требуется доказать, что φ удовлетворяет уравнению (3). По условию

F(t, φ(t), dt, φ′(t)dt, C) ≡ 0.

Заменив здесь t на s и dt на ds, получим тождество относительно s, ds:

F(s, φ(s), ds, φ′(s)ds, C) ≡ 0.

Оно показывает, что пара функций t = s, x = φ(s) образует решение уравнения (2s). Но тогда она должна быть и решением (3s):

G(s, φ(s), ds, φ′(s)ds, C1) ≡ 0.

Совершив обратную замену s на t и ds на dt, мы получим, что функция x = φ(t) удовлетворяет уравнению

G(t, φ(t), dt, φ′(t)dt, C1) ≡ 0.

Впредь, если не оговорено противное, мы будем всегда уравнения вида (1) рассматривать в симметричной трактовке, так как в этом случае все проведенные преобразования остаются справедливыми в обычной и обратной трактовках — в этом смысл доказанного утверждения.

1.3.3. Утверждение об уравнении в полных дифференциалах. Пусть (1) является уравнением в полных дифференциалах, т. е. существует такая дифференцируемая функция Φ(t, x), что

dΦ(t, x) = f(t, x)dx + g(t, x)dt    ((t, x) ∈ D(f) = D(g)).

Тогда следующее уравнение является его полным интегралом:

Φ(t, x) = C    (t, x ∈ D1).

(4)

Д о к а з а т е л ь с т в о.  Пусть функции t = ψ(s), x = φ(s) определены на некотором промежутке J ⊂ R. Тот факт, что пара (ψ, φ) есть решение уравнения (1) эквивалентен тождеству

[f(t, x)dx + g(t, x)dt]|t = ψ, dt = ψ′ds, x = φ, dx = φ′ds≡ 0,

которое, в свою очередь эквивалентно тождеству

[dΦ(t, x)]|t = ψ, dt = ψ′ds, x = φ, dx = φ′ds≡ 0.

Последнее в точности означает, что

d[Φ(t, x)]|t = ψ, x = φ ≡ 0  и  ψ, φ ∈ D1,

или, что то же,

Φ[ψ(s), φ(s)] ≡ C  и  ψ, φ ∈ D1.

Таким образом, (1) ⇔ (4).

Мы уже отмечали, что для уравнения с разделяющимися переменными f(x)dx – g(t)dt = 0 существует функция Φ(t, x) = F(x) – G(t), дифференциал которой совпадает с левой частью этого уравнения. Следовательно, это есть частный случай уравнения в полных дифференциалах. Отсюда вытекает, в частности, что доказанное в предыдущем параграфе утверждение об уравнении с разделенными переменными справедливо и в симметричной трактовке.

1.3.4. Пример: дифференциальное уравнение семейства концентрических окружностей. Рассмотрим уравнение (9) из п. 1.1.1:

x dx ds + y dy ds = 0.

Оно уже в своем первоначальном смысле является симметричным, т. е. содержит две неизвестные функции и не содержит явно аргумента s. Умножив обе части на ds, получим уравнение с разделяющимися переменными, которое в силу замечания, сделанного в конце предыдущего пункта, легко интегрируется:

x2 2 + y2 2 = C1   (x, y ∈ D1),

или

x2 + y2 = C   (x, y ∈ D1).

1.3.5. Признак полного дифференциала и алгоритм отыскания Φ(t, x). Будем предполагать, что в уравнении (1) функции f(t, x) и g(t, x) заданы на прямоугольнике J₁×J₂ (J₁, J₂ — промежутки в R) и непрерывны на нем вместе со своими частными производными ∂f/∂t и ∂g/∂x. Если в этих условиях (1) есть уравнение в полных дифференциалах, то

∂Φ ∂x  =  f, ∂Φ ∂t  =  g

(5)

и, следовательно,

∂f ∂t  =  ∂2Φ ∂t∂x ,   ∂2Φ ∂x∂t  =  ∂g ∂x .

Поэтому из известной теоремы о равенстве смешанных производных вытекает следующий необходимый признак уравнения в полных дифференциалах:

∂f ∂t  =  ∂g ∂x    ((t, x) ∈ J1×J2).

(6)

Мы сейчас покажем, что он является и достаточным, и заодно опишем алгоритм нахождения функции Φ(t, x). Будем считать в уравнении (5) переменную t параметром, x — аргументом, Φ — неизвестной функцией. Тогда

Φ = ∫ x x0 f(t, ξ) dξ + C(t)

и

∂Φ ∂t = ∂ ∂t ∫ x x0 f(t, ξ)  dξ + C′(t) = g(t, x),

т. е.

C′(t) = g(t,x)  –  ∂ ∂t ∫ x x0 f(t, ξ)  dξ.

Воспользовавшись известным правилом Лейбница дифференцирования интеграла по параметру, получим

∂ ∂t ∫ x x0 f(t, ξ) dξ  =  ∫ x x0 ∂f(t, ξ) ∂t dξ  =  ∫ x x0 ∂g(t, ξ) ∂ξ dξ  = g(t, x) – g(t, x0).

Поэтому

C′(t) = g(t, x0), C(t) = ∫ x x0 g(s, x0) ds + C1.

Таким образом, при выполнении условия (6) в качестве Φ можно взять функцию

Φ(t, x) = ∫ x x0 f(t, ξ) dξ + ∫ x x0 g(s , x0) ds,

(7)

где t₀, x₀ — произвольные фиксированные точки промежутков J₁ и J₂, соответственно.

Итак, если f и g непрерывны на J₁×J₂ вместе с ∂f/∂t и ∂g/∂x и удовлетворяют условию (6), то (1) есть уравнение в полных дифференциалах, для которого функция Φ находится с помощью описанного алгоритма или непосредственно по формуле (7).

1.3.6. Пример. Решим уравнение

(3t2 – x2)dt + (3x2 – 2tx)dx = 0.

(8)

Для него

g(t, x) = 3t2 – x2;    ∂g ∂x = – 2x;

f(t, x) = 3x2 – 2tx;    ∂f ∂t = – 2x.

Условие полного дифференциала (6) выполнено в D = R×R. Найдем Φ(t, x). Поскольку

∂Φ ∂x = 3x2 – 2tx,

очевидно

Φ = ∫ x x0 (3ξ2 – 2tξ) dξ + C(t) =

= [ξ3 – tξ2]| x x0 + C(t) = x3 –  tx2 + C(t).

а так как

∂Φ ∂t = – x2 + C′(t) = 3t2 x2,

очевидно, C′(t) = 3t². Поэтому C(t) = t³ + C₁ и, следовательно, Φ(t, x) = x³ – tx² + t³. Мы нашли полный интеграл:

x3 – tx2 + t3 = C   (t, x ∈ D1).

1.3.7. Интегрирующий множитель. Если для уравнения (1) условие полного дифференциала (6) не выполнено, то иногда удается найти функцию μ = μ(t, x), такую, что для уравнения

μ · f(t, x)dx + μ · g(t, x)dt = 0

(9)

оно уже выполнено. В этом случае функция μ называется интегрирующим множителем. Общего способа нахождения интегрирующего множителя не существует, однако можно указать простые признаки существования и прием построения интегрирующих множителей, зависящих только от x или только от t.

Если, например, считать, что μ зависит только от x, то

∂μ · f ∂t = μ ∂f ∂t = ∂μ · g ∂x = μ′ + μ ∂g ∂x ,

и аналог условия (6) для (9) выглядит так:

μ′ = [ ( ∂f ∂t  –  ∂g ∂x ) / g ] · μ.

(10)

Если выражение в квадратных скобках не зависит от t, то (10) есть линейное однородное уравнение относительно μ = μ(x); оно легко решается и дает интегрирующий множитель для (1).

Аналогично ищется интегрирующий множитель, зависящий только от t.

1.3.8. Пример. Найдем интегрирующий множитель μ = μ(x) для уравнения

(3t2/x2 – 1)dt + (3 – 2t/x)dx = 0

(11)

(оно получено почленным делением уравнения (8) на x², поэтому мы заранее знаем, что интегрирующий множитель μ = x² существует). Выпишем для уравнения (11), умноженного почленно на μ, условие полного дифференциала:

∂μ · (3 – 2t/x) ∂t = μ · ( – 2 x ) ;

∂μ · (3t2/x2 – 1) ∂x = μ′(3t2/x2 – 1) + μ · ( – 6t2 x3 ) ;

μ′ = [ ( – 2 x + 6t2 x3 ) / (3t2/x2 – 1) ] · μ = 2 x μ.

Поскольку выражение в квадратных скобках оказалось не зависящим от t, искомый интегрирующий множитель существует и находится из уравнения:

∂μ μ = 2dx x ;   μ = Cx2.

В частности, мы получили уже известный нам заранее интегрирующий множитель μ = x².

1.3.9. Обобщенное утверждение об уравнении в полных дифференциалах. Пусть в уравнении

f1(x)dx1 + f2(x)dx2 + ... + fn(x)dxn = 0

(12)

функции f_i(x) = f_i(x₁, ..., x_n) непрерывны вместе со своими частными производными ∂f_i/∂x_k (i ≠ k) на декартовом произведении интервалов J₁ × J₂×... × J_n = D.

Тогда левая часть уравнения (12) будет полным дифференциалом некоторой функции Φ(x) в том и только том случае, если

∂Φi ∂xk = ∂Φk ∂xi    (i, k = 1, 2, ..., n;  i ≠ k; x ∈ D).

При этом функция Φ находится по формуле

Φ(x) = n ∑ k = 1 ∫ xk x0k f(x1, ..., xk–1, ξ, x0k+1, ..., x0n)  dξ

(x0k ∈ Jk — произвольные фиксированные точки), а полный интеграл уравнения (12) можно записать в виде

Φ(x) = C    (x ∈ D1).

В частности, условиям данной теоремы удовлетворяет уравнение с разделенными переменными

f1(x1)dx1 + f2(x2)dx2 + ... + fn(xn)dxn = 0,

если функции f_k: J_k → R непрерывны; полный интеграл имеет вид

F1(x1) + F2(x2) + ... + Fn(xn) = 0,

где F_k — первообразная f_k (k = 1, ..., n).

1.3.10. Пример: уравнение гармонического осциллятора. Умножив обе части известного из школьного курса физики уравнения гармонического осциллятора

x′′ + ω2x = 0

(13)

на dx, получим

x′′dx + ω2xdx = 0.

(14)

Заметив, что x′′dx = x′′x′dt = x′dx′, мы придем к уравнению вида (12):

x′dx′ + ω2xdx = 0

(в нем n = 2, x₁ = x′, x₂ = x). Его эквивалентный интеграл есть

(x′)2 2 + ω2x2 = C.

(15)

Таким образом, мы понизили порядок уравнения (13). Физически полученное уравнение (15) выражает закон сохранения энергии.

В вышеприведенных преобразованиях (13) ⇒ (14), (14) ⇔ (15), но (14) 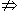(13).

1.3.11. Контрольные вопросы

1.3.11.1. Пусть функции t = ψ(s), x = φ(s) — решения уравнения (2) в симметричной трактовке. Является ли график кривой, параметрически заданной функциями t = ψ(s), x = φ(s), интегральной кривой этого уравнения?

1.3.11.2. Являются ли уравнения

dx dt = x  и  x dt dx = 1

эквивалентными в обычной, обратной и симметричной трактовках?

1.3.11.3. Уравнение x = C₁t + C₂ в обычной трактовке является следствием уравнения d²x/dt² = 0. Покажите, что это не так в симметричной трактовке (У к а з а н и е: пара функций t = s², x = s² является решением первого уравнения, но не решением второго. Вспомните неинвариантность формы высших дифференциалов!)

1.3.11.4. Приведите пример функции, являющейся решением уравнения (14), но не являющейся решением уравнения (13).

1.3.11.5. Найдите общий интеграл уравнения (t – x)dx + (t² + x)dt = 0.

1.3.11.6. Почему рассуждения в п. 1.3.5 в части достаточности нельзя провести в случае, когда область определения функций f и g не является односвязной?

1.3.11.7. Найдите интегрирующий множитель в случае, когда выражение, стоящее в квадратных скобках в (10), зависит только от t.

1.3.12. Задачи

1.3.12.1. Докажите следующее обращение утверждения о симметричной трактовке для уравнений первого порядка: если (2) ⇒ (3), то (2s) ∧ (x′ ≠ 0) ⇒ (3s). Пример, приведенный в контрольном вопросе 3 показывает, что, вообще говоря, (2s) (3s).

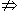
1.3.12.2. Докажите сформулированное в п. 1.3.9 утверждение.

1.3.12.3. Докажите, что уравнение семейства овалов Кассини

(x2 + t2 + a)xx′ + (x2 + t2 – a)t = 0

есть уравнение в полных дифференциалах. Найдите полный интеграл.

1.3.12.4. Найдите форму зеркала, отражающего все лучи, падающие на него из заданной точки, параллельно заданному направлению.

1.3.12.5. Покажите, что если μ = μ(t, x) — интегрирующий множитель уравнения (1), то для любой непрерывной отличной от нуля функции h функция M(t, x) = h[Φ(t, x)]μ(t, x), где dΦ = μf·dx + μg·dt, также является интегрирующим множителем.

1.3.12.6. Пусть непрерывная функция h и непрерывно дифференцируемая функция H таковы, что

∂f(t, x) ∂t   –   ∂g(t, x) ∂x g(t, x) ∂H(t, x) ∂x   –  f(t, x) ∂H(t, x) ∂t ≡ h[H(t, x)].

Покажите, что функция μ(t, x) = M[H(t, x)], где

M(s) = exp ( ∫ h(s) ds ) .

является интегрирующим множителем уравнения (1).

1.3.12.7. Покажите, что если Φ(t,x) — полный интеграл уравнения (1), то функции [∂Φ(t, x)/∂t]/g(t, x) и [∂Φ(t, x)/∂x]/f(t, x) совпадают и являются интегрирующим множителем этого уравнения.

File based on translation from T_EX by T_TH, version 2.32.
Created On 1 Jan 2002, 23:21.
Last modified 9 Apr 2002.