§ О10. Метод функций Ляпунова

Метод исследования устойчивости по первому приближению является мощным, но не универсальным. В некоторых случаях он не может дать ответ на вопрос об устойчивости решения. Например, это так для уравнения маятника без трения

xў1= x2,    xў2= –sin x1,

(1)

поскольку собственные значения линеаризованной в нижнем положении равновесия системы

xў1= x2,    xў2= –x1

лежат на мнимой оси.

Здесь мы описываем один метод исследования устойчивости, восходящий к выдающемуся русскому математику А.М. Ляпунову — так называемый метод функций Ляпунова (или второй метод Ляпунова).

Мы будем рассматривать уравнение

xў = f(t, x)

(2)

(f: R×Rⁿ ® Rⁿ).

Непрерывно дифференцируемая на открытом подмножестве D М R×Rⁿ скалярная функция V называется функцией Ляпунова системы (2), если при всех (t, x) О D

¶V(t, x) ¶t + ж и ¶V(t, x) ¶x , f(t, x) ц ш Ј 0

(3)

(здесь и ниже (·,·) — скалярное произведение в Rⁿ). Левая часть неравенства (3) иногда называют производной функции V в силу уравнения (1)

Задача О10.1. Докажите, что если в последнем соотношении заменить знак неравенства на равенство, то функция V будет первым интегралом.

Функции Ляпунова, в отличие от первых интегралов, обладают тем свойством, что вдоль любого решения j уравнения (2) они не возрастают. Действительно,

dV[t, j(t)] dt = ¶V(t, x) ¶t к к x= j(t) + ж и ¶V(t, x) ¶x к к x= j(t) , jў(t) ц ш =

= ¶V(t, x) ¶t к к x= j(t) + ж и ¶V(t, x) ¶x к к x= j(t) , f[t, j(t)] ц ш Ј 0.

Грубо говоря, это свойство означает, что решения (2) "протыкают" поверхности уровня "в одном направлении" — со стороны бóльших значений в сторону меньших. Геометрически, этот факт легче представить в случае автономной (т. е. не зависящей от t) функции Ляпунова, рассматривая траектории в фазовом пространстве, а не интегральные кривые в расширенном фазовом пространстве. На рис. 1 изображены линии уровня некоторой автономной функции Ляпунова (внутренние линии отвечают меньшим значениям). Траектория, попав на какую-либо линию уровня, уже не может покинуть область, ограничиваемую этой линией.

Рис. 1.

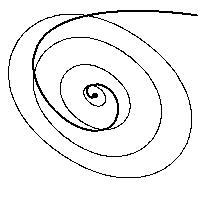
Подчеркнем, что для построения функций Ляпунова (т. е. нахождения функций, удовлетворяющих (3)) не требуется знать решения уравнения.

В дальнейшем мы, для простоты, будем рассматривать только автономные уравнения

xў = f(x)

(4)

(f: Rⁿ ®Rⁿ) и автономные функции Ляпунова. Соотношение (3) для них, очевидно, выглядит так

ж и ¶V(x) ¶x , f(x) ц ш Ј 0.

Всюду ниже предполагается, что нуль является положением равновесия системы (4) (т. е. f(0) = 0); его устойчивостью мы и интересуемся.

Предположим, что нам удалось подобрать такую функцию Ляпунова V, что V(0) = 0, а множества U_e = {x О Rⁿ: V(x) Ј e} при малых положительных e "подобны" малым окрестностям нуля в Rⁿ (составляют базу окрестностей нуля). Тогда, поскольку функция Ляпунова вдоль решения не возрастает, любое решение, начальное значение которого лежит в U_e, остается в нем при t > 0 (см. рис. 2); по существу, это означает устойчивость нулевого решения. Множества U_e обладают нужным свойством, например, если 0 — точка строгого локального минимума функции V (см. рис. 3).

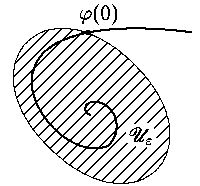Рис. 2.

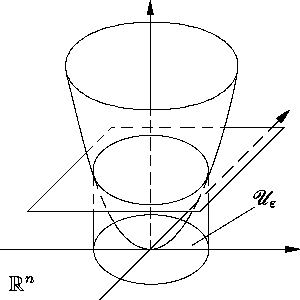Рис. 3.

Если же дополнительно

ж и ¶V(x) ¶x , f(x) ц ш < 0.

при всех x № 0, то функция V(x) вдоль решений, как нетрудно видеть, строго убывает и, следовательно, при возрастании t точка j(t) попадает во множества U_e со все меньшими e. А так как U_e "стягиваются" к нулю, то вместе с ними стремится к нулю и решение j(см. рис. 1). Последнее означает асимптотическую устойчивость системы (4).

Эти простые геометрические соображения формализуются в следующих двух теоремах.

Теорема Ляпунова об устойчивости. Пусть в окрестности D нуля в Rⁿ существует автономная функция Ляпунова системы (4) такая, что V(0) = 0 и V(x) > 0 при x ОD \{0}. Тогда нулевое положение равновесия этой системы устойчиво по Ляпунову.

Д о к а з а т е л ь с т в о.  Зафиксируем произвольное положительное e (при этом будем считать, что шар B(0,e) целиком лежит в D) и положим

a = {V(x): ||x|| = e}.

Число a положительно.

Задача О10.2. Почему?

Из непрерывности V вытекает наличие d1 > 0 такого, что V(x) < a при ||x|| < d1. Покажем, что произвольное положительное d, меньшее min{e, d1}, является искомым, т. е. покажем, что из неравенства ||u|| < d следует неравенство ||gt0t(u)||< e при всех t і t0. В предположении противного найдутся u0, ||u0|| < d и t1 > t0 такие, что ||j(t1)|| і e (здесь j(t) = gt0t(u0)). В силу непрерывности ||j(t)|| можно указать t2 О (t0, t1] такое, что

||j(t)|| < e при t О [t0, t2] и ||j(t2)|| = e.

Поскольку V не возрастает вдоль решений

V[j(t2)] Ј V[j(t0)] = V(u0),

а так как ||u₀|| < d и, следовательно, V(u₀) < a,

V[j(t2)] < a.

С другой стороны, так как||j(t₂)|| = e, по определению a

V[j(t2)] і a.

Противоречие.

Задача О10.3. Докажите, что нижнее положение равновесия маятника без трения (система (1)) устойчиво (для этого покажите, что его полная энергия является функцией Ляпунова).

Теорема Ляпунова об асимптотической устойчивости. Пусть в дополнение к условиям предыдущей теоремы

W(x)   = def   ж и ¶V(x) ¶x , f(x) ц ш < 0

(5)

при x О D \{0}. Тогда нулевое решение системы (4) асимптотически устойчиво.

Д о к а з а т е л ь с т в о.  Нам нужно показать только, что

j(t) ® 0 при t ® +Ґ,

(6)

если j(t₀) достаточно малó. Зафиксируем положительное e такое, чтобы B(0, e) М D и построим по нему d как в доказательстве предыдущей теоремы. Покажем, что при ||j(t₀)|| < d выполнено (6), для чего покажем сначала, что

V[j(t)] ® 0 при t ® +Ґ.

(7)

Функция V[j(t)] не возрастает и, более того,

dV[j(t)] dt = W[j(t)] < 0,

если j(t) № 0. Поэтому либо, начиная с некоторого t₁ > t₀, функция V[j(t)] тождественно нулевая (и тогда (7) доказано), либо она строго убывает. Таким образом, предел a = lim_t®+ҐV[j(t)] существует. Допустим, что (7) не выполнено, т. е. a > 0. Тогда

(e і) ||j(t)|| і b > 0.

Действительно, в противном случае нашлась бы такая последовательность t_k ® Ґ такая, что j(t_k) ® 0 при k ® Ґ. Вместе с ней, силу непрерывности функции V, к нулю стремилась бы и последовательность V[j(t_k)], что противоречит неравенству a > 0.

Положим теперь

a1 = sup{W(x): b Ј ||x|| Ј e}.

Число a₁ отрицательно, так как иначе функция W обращалась в нуль при некотором x № 0. Но тогда

V[j(t)] = V[j(t0)] + т t t0 dV[j(s)] ds ds =

= V[j(t0)] + т t t0 ж и ¶V[j(s)] ¶x ,  dj(s) ds ц ш ds = V[j(t0)] + т t t0 W[j(s)] ds Ј

Ј V[j(t0)] + т t t0 a1 ds = V[j(t0)] + a1t ® –Ґ при t ® +Ґ.

Последнее противоречит неотрицательности функции V.

Осталось показать, что из (7) следует (6). Если это не так, то найдутся t_k ® +Ґ и g > 0 такие, что

(e і) ||j(tk)|| і g.

Но тогда выполнено неравенство

V[j(tk)] і a2   =  def inf{V(x): g Ј ||x|| Ј e} > 0,

которое в силу (7) невозможно. Теорема доказана.

С помощью функций Ляпунова можно также исследовать неустойчивость решений. Мы ограничимся формулировкой одной простейшей теоремы и ее геометрической иллюстрацией.

Теорема Ляпунова о неустойчивости. Пусть функция Ляпунова V системы (4) удовлетворяет (5) и такова, что в любой окрестности нулевого положения равновесия есть точки, в которых она отрицательна. Тогда нулевое решение этой системы неустойчиво.

Геометрическая суть этой теоремы изображена на рис. 4.

Рис. 4.

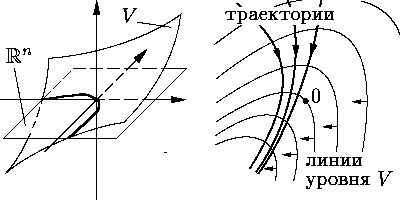
В некотором смысле описанные теоремы Ляпунова допускают обращение. Грубо говоря, условия этих теорем являются необходимыми: если положение равновесия обладает теми или иными свойствами устойчивости, то у системы существует удовлетворяющая соответствующим требованиям функция Ляпунова. В качестве простейшего примера покажем, что если линейная автономная система

xў = Ax

(8)

асимптотически устойчива, то у нее существует положительная в Rⁿ\{0} функция Ляпунова, удовлетворяющая (5). В самом деле, асимптотическая устойчивость гарантирует, что все собственные значения матрицы A имеют отрицательные вещественные части и, следовательно, система экспоненциально устойчива. Пусть F(t) — нормальная в нуле фундаментальная матрица этой системы (F(t) = e^At). Экспоненциальная устойчивость гарантирует наличие положительных M и a таких, что

||F(t)|| Ј Me–at при t і 0.

Положим

V(x) = т Ґ 0 ||F(s)x||2ds.

Задача О10.4. Покажите, что V(x) = (S(x),x), где S = т0ҐF*(s)F(s) ds.

Функция V(x) очевидно положительна в Rⁿ\{0}. Остается заметить, что

ж и ¶V(x) ¶x , f(x) ц ш  =  ж и ¶ ¶x т Ґ 0 ||eAsx||2 ds, Ax ц ш =

=  т Ґ 0 ж и ¶ ¶x || eAsx||2, Ax ц ш ds  =  т Ґ 0 2(eAsx, AeAsx) ds =

=  т Ґ 0 d ds (eAsx, eAsx) ds = –||x||2.

Задача О10.5. Проведите подробные вычисления.

Возможность обращения теорем Ляпунова позволяет, в частности, реализовать следующую (предложенную А.М. Ляпуновым) схему доказательства теорем об устойчивости и неустойчивости по первому приближению. Если, например, линеаризованное уравнение асимптотически устойчиво, то для него существует функция Ляпунова, обладающая соответствующими свойствами. Эта функция оказывается и функцией Ляпунова исходной системы. Поэтому из соответствующей теоремы Ляпунова вытекает устойчивость нулевого решения нелинейной системы.

Литературные указания. Теория функций Ляпунова восходит к классической книге А.М. Ляпунова [Ляпунов], являющейся его диссертацией. Фрагмент из этой книги мы приводим в избранном. Для начального изучения рекомендуется книга [Демидович]. Различным аспектам теории функций Ляпунова посвящены монографии [Барбашин: Введение..., Барбашин: Функции..., Валеев — Финин, Красовский, Ла-Салль — Лефшец, Ляпунов, Малкин, Руш — Абетс — Лалуа, Четаев].

Задачи. О10.6. Пусть система (4) имеет непостоянный автономный первый интеграл. Докажите что нулевое положение этой системы не является асимптотически устойчивым в целом.

О10.7. Покажите, что если квадратичная форма (Ax, x) неположительна, то система (8) устойчива.

О10.8. Покажите, что если квадратичная форма (Ax, x) отрицательно определена, т. е. (Ax, x) Ј –r||x||² (r > 0), то при любом b О Rⁿ нулевое решение системы xў = Ax + b||x||² асимптотически устойчиво.

В дальнейшем считается, что f в (2) удовлетворяет условиям теоремы Коши — Пикара и f(t, 0) є 0.

О10.9. Докажите, что нулевое решение этой системы устойчиво в том и только том случае, если она имеет невырожденный первый интеграл V: R×Rⁿ ® Rⁿ удовлетворяющий условиям: а) V(t, 0) є 0; б) V непрерывен по второму аргументу; в) если V(t_k, x_k) ® 0 при k ® Ґ, то x_k ® 0 при k ® Ґ.

О10.10. Докажите следующие обобщения теорем Ляпунова на неавтономные системы. Если уравнение (2) имеет функцию Ляпунова V: R×Rⁿ ® Rⁿ и существует определенная в окрестности D нуля скалярная функция W такая, что

V(t, x) і W(x) > 0 при всех t і 0, x О D\{0},

V(t, 0) є W(0) = 0,

то нулевое решение системы (2) устойчиво по Ляпунову.

Если же дополнительно

¶V(t, x) ¶t + ж и ¶V(t, x) ¶x ,  f(t, x) ц ш Ј –W(x)

при всех t, x и

V(t, x) ® 0 при x ® 0

равномерно по t, то нулевое решение системы (2) асимптотически устойчиво.

File based on translation from T_EX by T_TH, version 2.32.
Created 19 Jan 2000, 06:57.
Last modified 8 Apr 2002.