|
2.2.8. Аппроксимация параболического дифференциального оператора
¶/¶t – ¶2/¶x2 |  |
Пусть теперь W = (0, X) × (0, T), u: W ® R — достаточно гладкая функция (u = u(x, t)), F(W) состоит из достаточно
гладких функций, а L — параболический
дифференциальный оператор на F(W): Lu = ¶u/¶t – ¶2u/¶x2.
Пусть, далее, wht — прямоугольная равномерная сетка на W с шагами h и t по x и t соответственно. Как и выше, будем сохранять обозначение xij для точек (ih, jt) (i = 0, ...,
n, j = 0, ..., m) сетки.
|
Как и в п. 2.2.6, оператор L предстáвим в виде разности операторов L1 =
¶/¶t и L2
= ¶2/¶x2. Если мы теперь аппроксимируем оператор L1 одним из операторов L1t+,L1t–или L1t°,а оператор L2 — оператором L2h°,то получим следующие три аппроксимации оператора L: |
|
Lh°t+u= L1t+u– L2h°u= ut+– ux–x+, | (4) |
|
Lh°t–u= L1t–u– L2h°u= ut–– ux–x+, | (5) |
и
|
Lh°t°u= L1t°u– L2h°u= ut°– ux–x+, | (6) |
Соответствующие им шаблоны изображены на рис. 2.2а, 2.2б и 2.2в.
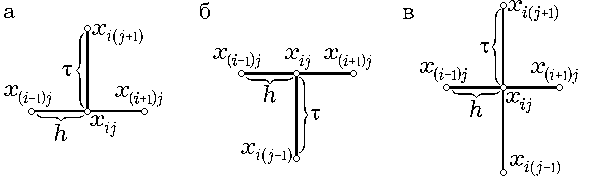
Рис. 2.2.
Так же, как и в теореме 2.2.3, без труда доказывается, что для достаточно гладких функций u
а