2.1.2. Сетки на плоскости (x, t)

Если рассматривается функция, область определения которой представляет собой прямоугольник W = {(x, t) О [0, X] × [0, T]}, то равномерную сетку на W можно определить так. Для любых n, m О N положим h = X/n, t = T/m, x_i = ih (i = 0, 1, ..., n), t_j = jt (j = 0, 1, ..., m). Равномерную ортогональную сетку w_ht на W, по определению, образуют точки (x_i, t_j): i = 0,1, ..., n, j = 0, 1, ..., m (см. рис. 1.2). Числа h и t называются шагами сетки (по x и t). Такую сетку иногда удобно представлять как декартово произведение равномерной сетки w_h на отрезке [0, X] и равномерной сетки w_t на отрезке [0, T]: w_ht = w_h × w_t.

Рис. 1.2.

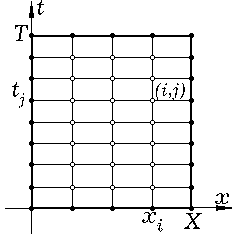
В некоторых случаях (когда важно более точно аппроксимировать искомую функцию в окрестности каких-либо точек или линий) приходится рассматривать неравномерные ортогональные сетки, отличающиеся от равномерных только тем, что в произведении w_ht = w_h × w_t сетки w_h и w_t неравномерные.

Более того, в ряде случаев приходится использовать неортогональные сетки. Примером такой сетки может служить сетка, представленная на рис. 1.3. Работа с такими сетками существенно сложнее, как в идейном, так и в алгоритмическом плане, но в некоторых задачах они — единственный на настоящий момент вариант.

Рис. 1.3.

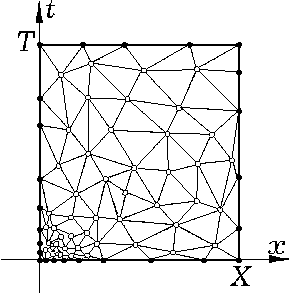
Различают внутренние узлы и граничные узлы сетки (первые изображены светлыми, а вторые черными точками на рис. 1.2 и 1.3). Первые характеризуются тем, что лежат внутри W, а вторые — на G.