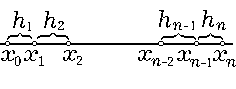|
Допустим, область изменения интересующей нас функции представляет
собой отрезок [0, X] М R. Пусть для любого n О N+ определено
упорядоченное множество {hi}ni=1положительных чисел, причем еni=1hi= X. Набор точек w = {xk = еki=1hi}nk=0(здесь, по определению, е0i=1hi= 0) называется сеткой (см. рис. 1.1). Числа hi
называются шагами сетки, а точки xi — узлами сетки. Если все hi одинаковы:
hi є h = X/n (при фиксированном n), то говорят о
равномерной сетке, или сетке с постоянням шагом h. |