2.1.3. Сетки на плоскости x

В случае, когда рассматриваемая область W представляет собой прямоугольник [0, X₁] × [0, X₂], по существу, нет никаких отличий от случая, рассмотренного в предыдущем пункте.

Если же область W представляет собой область сложной конфигурации, что отнюдь не редкость в практических задачах, то приходится так или иначе приспосабливаться к новой ситуации. Простейший из вариантов таков. Разобъем оси 0x₁ и 0x₂ отрезками длины h₁ и h₂ и проведем через концы отрезков прямые, параллельные, соответственно осям 0x₂ и 0x₁. Из узлов получившейся равномерной прямоугольной решетки выберем узлы, лежащие внутри W и отнесем их к внутренним узлам сетки (светлые точки на рис. 1.4). Точки пересечения прямых решетки с границей области отнесем к граничным узлам (темные точки на рис. 1.4). Множество внутренних узлов обозначим через w, граничных — через g, а множество w И g всех узлов сетки — через w. Отметим, что хотя в рассматриваемом примере шаги по x₁ и x₂ регулярны (одинаковы в каждом направлении) и, следовательно, сетка w внутренних узлов может считаться регулярной, вся сетка w целиком регулярной не является, и, в частности, не может быть представлена в виде декартова произведения сеток по x₁ и x₂.

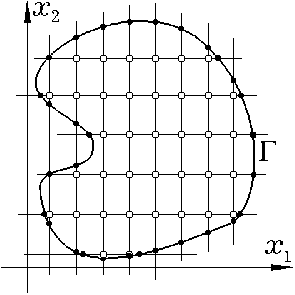
Рис. 1.4.

Точно так же, как и выше на x-плоскости можно рассматривать прямоугольные сетки с неравномерными шагами, а также нерегулярные сетки. Вообще следует заметить, что вопрос о классификации сеток далек от своего разрешения. В дополнение к вышеприведенным сеткам, некоторые из возможных сеток см. на рис. 1.5.

Рис. 1.5.

Ничем, кроме меньшей наглядности и более сложной структуры, не отличаются сетки в трехмерном пространстве и в пространстве R³ × R.