Разработан подход построения неявных схем высоких порядков аппроксимации для решения квазилинейных систем уравнений сжимаемого газа, основанный на применении симметричных консервативных разностных формул высоких порядков для пространственных производных первой степени и адаптивных слагаемых искусственной вязкости. Целью исследования является построение схем повышенной точности без осцилляций на разрывах и с хорошей сходимостью по времени. Предлагается использование скалярной адаптивной диффузии, имеющей высокий порядок малости на гладких участках решения, первый порядок возле разрывов решения и обладающей отрицательной диссипацией определенной математической "энергии". Подход опробован на двухслойной неявной схеме третьего порядка по пространственным переменным, неявной схеме предиктор-корректор пятого порядка по пространственным переменным и неявной схеме Рунге-Кутты третьего порядка по всем переменным. Во всех случаях результаты оказались успешными. На сетке 45х60 при расчете разрывного решения для достижения величины невязки порядка машинного нуля требуется 230 итераций для схемы третьего порядка и 1000-3000 итераций для схемы пятого порядка и схемы Рунге-Кутты. Построенные численные алгоритмы применены для исследования гиперзвуковых течений возле тел вращения с передним аэродинамическим элементом, индуцирующим образование отрывной зоны.

Проведено теоретическое исследование условий возникновения и качественной структуры степенных пограничных и внутренних слоев в сингулярно возмущенных системах обыкновенных дифференциальных уравнений.

Изучено влияние некоторых геометрических характеристик координатных поверхностей на качество пространственных структурных сеток. Получены уравнения для конструирования структурных сеток, учитывающие в явном виде среднюю кривизну мониторной поверхности.

Построена модификация кубического нелокального сплайна, обеспечивающая сохранение направления роста интерполируемых функций.

Разработана и исследована конечно-разностная схема второго порядка аппроксимации, являющаяся обобщением известной схемы Хартена на случай подвижных адаптивных сеток. Получены условия, при которых схема удовлетворяет условию TVD. Проведено тестирование построенной схемы путем численного решения уравнения Хопфа и системы уравнений мелкой воды. Результаты тестирования показали, что применение построенной TVD схемы на подвижных сетках дает существенную экономию машинного времени по сравнению со схемой Хартена, предназначенной для расчетов на равномерных сетках (рис. 1).

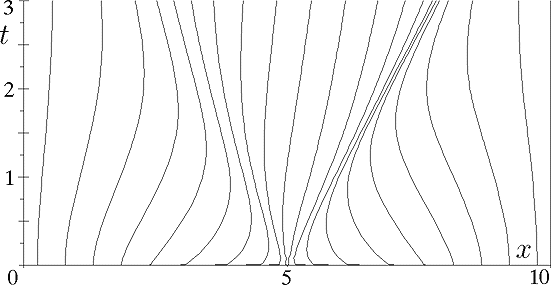
Рис. 1. Сравнение численного и точного решения задачи о распаде разрыва и траектории узлов адаптивной сетки, использованной в расчете.

Продолжено исследование компактных разностных схем повышенного порядка точности для уравнений второго порядка в ортогональных системах координат. В случае краевых задач для эллиптических и параболических уравнений рассмотрены вопросы постановки достаточно точных конечных соотношений на оси и в центре наиболее употребительных криволинейных систем координат (полярной, цилиндрической и сферической) для их использования в качестве граничных условий в ранее разработанных компактных схемах. При этом рассмотрены как симметричные (не зависящие от угловых переменных), так и произвольные несимметричные краевые задачи. Во всех случаях решен вопрос о выборе наиболее подходящей формы факторизованного оператора, действующего на верхнем шаге, который обеспечивал бы естественную реализацию граничных условий для схемы в дробных шагах.

Продолжены исследования, направленные на разработку компактных схем на прямоугольных неравномерных сетках. Схемы третьего порядка аппроксимации, построенные ранее для одномерного нелинейного уравнения с конвективным и диссипативным членами и для модельного двумерного уравнения с постоянными коэффициентами, удалось распространить в плоском случае на систему стационарных уравнений Навье-Стокса в переменных функция тока и вихрь скорости.

Было продолжено исследование проблемы построения схем, максимально точно аппроксимирующих эллиптическое уравнение на нерегулярном шаблоне с заданным числом практически произвольно расположенных точек плоскости. Выявлена зависимость порядка аппроксимации от числа точек шаблона при небольшом числе точек, и рассмотрены частные случаи расположения точек шаблона, повышающие порядок аппроксимации.

Разработаны алгоритмы и проведено сравнение двух численных методов решения многоточечных краевых задач для систем нелинейных обыкновенных дифференциальных уравнений высокого порядка с переменными коэффициентами, основанных на методах сплайн-коллокации и дискретной ортогонализации С.К.Годунова и описывающих напряженно-деформированное состояние сопряженных композитных конструкций.

Исследовано влияние геометрической нелинейности и внутренней структуры композиционного материала на вид напряженно-деформированного состояния армированных сосудов высокого давления, резервуаров для хранения жидкостей, полученных последовательным сопряжением через шпангоуты оболочек вращения. Показано хорошее совпадение результатов, полученных разными методами.

На рис. 2 представлены зависимости максимальных значений приведенных напряжений в связующем материале bs₀, спиральной bs₁ и окружной арматуре bs₂ от угла укладки спирального семейства арматуры 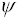. Кривые 1, 2, 3 соответствуют различным комбинациям удельных интенсивностей армирования. Пунктирным линиям соответствуют значения, рассчитанные по линейной модели, а сплошным – по нелинейной модели. Из рис. 2 следует,

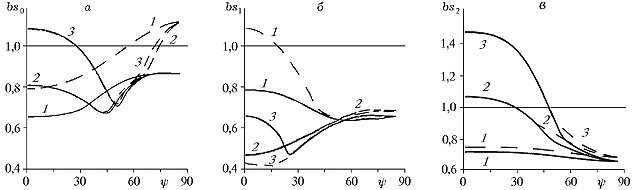
Рис.2.

что уровень напряжений в связующем материале и в спиральном семействе арматуры существенным образом зависит как от выбора геометрической модели оболочки, так и от структуры армирования, тогда как на уровень напряжений в окружном семействе арматуры выбор геометрической модели влияет незначительно.

Исследовано напряженно-деформированное состояние и определены параметры начального разрушения армированного термоупругого диска. Опираясь на результаты численных расчетов, показана целесообразность использования геометрически нелинейной теории композитного диска.

На рис. 3, 4 показано влияние угла укладки спиральной арматуры на величины максимальных приведенных напряжений в связующем материале и спиральных волокнах при фиксированных значениях интенсивностей армирования, из которых следует, что укладывая спиральные волокна в интервале от 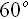до 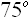, можно почти в 2 раза снизить уровень максимальных напряжений в диске, обеспечив тем самым упругую работу композиционного материала.

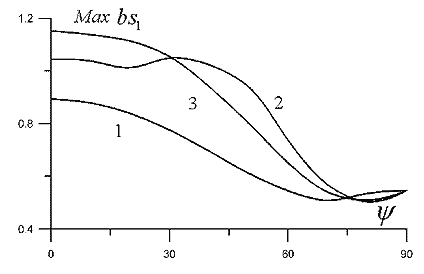
Рис.3.

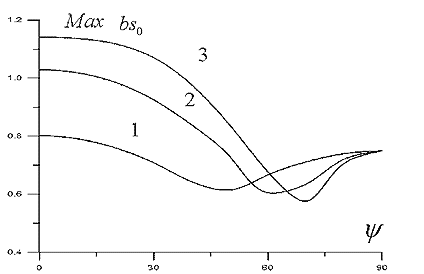
Рис. 4.

Для нелинейно-дисперсионных уравнений волновой гидродинамики разработан дискретный алгоритм на базе метода конечных элементов и метода конечных объемов. Первый из них применяется для нахождения скорости из уравнения движения, а второй используется для аппроксимации уравнения неразрывности. Выполнены расчёты (см. рис. 5) модельных волновых полей, возникающих при взаимодействии с островами цилиндрического и конического сечений. Расчетные кривые максимального заплеска хорошо воспроизводят тенденции экспериментальных данных.

Создан пакет программ реализующий метод частиц для решения задачи динамики бесстолкновительной плазмы с учетом конечности ионного ларморовского радиуса на мультикомпьютерах Parsytec PowerXplorer, Cray T3D. Программы динамически настраиваются на сложившиеся распределения частиц, объем памяти и число процессорных элементов.

Работа выполнена в сотрудничестве с ИВМиМГ СО РАН.

Создана численная модель, использующая приближение бесстолкновительной плазмы и позволяющая исследовать аномальную теплопроводность плазмы, нагреваемую релятивистским электронным пучком. Постановка задачи соответствует условиям лабораторных экспериментов, проводимых в ИЯФ СО РАН на установке ГОЛ-3-II. Проведенная серия вычислительных экспериментов демонстрирует подавление электронной теплопроводности во время релаксации пучка.

Для отдельных классов инвариантных решений полного кинетического уравнения Больцмана со степенным потенциалом межмолекулярного взаимодействия, зависящих от одной инвариантной переменной, выведены фактор – уравнения и исследовано существование их обобщенных решений.

Выполнено численное моделирование радиального плазмохимического реактора с целью сравнения наиболее употребительных упрощенных кинетических моделей для тетрафторида углерода. Результаты расчетов для 2х-, 3х- и 4х-компонентной кинетик показывают, что для разных моделей имеют место значительные расхождения в значениях концентраций фтора и скорости травления образца (см. рис. 6). Этим поставлен вопрос о критической оценке результатов, полученных на основе различных кинетик, и необходимости выбора адекватной кинетической модели на базе экспериментальных данных.

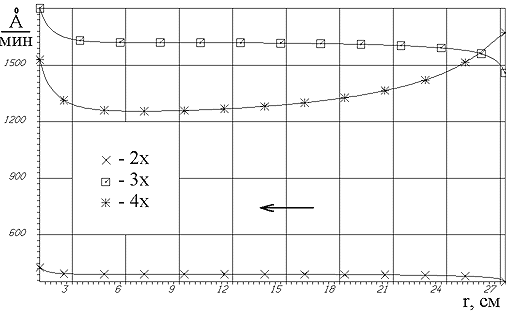
Рис. 6. Распределение скорости спонтанного травления вдоль радиуса образца для 2х-, 3х- и 4х-компонентной кинетик в радиальном реакторе травления. Направление течения газа обозначено стрелкой. Расчетный режим: T_e = 5.9 эВ, p = 0.512 торр, Q = 340 см³/мин, T_s = 473 K.

Изучалась задача о бессдвигом слое смешения между потоками жидкости, различающимися масштабом турбулентности. Для исследования задачи привлекалась модель третьего порядка. В случае однородной жидкости доказано существование автомодельного решения. Установлено, что алгебраическое выражение для моментов 3-го порядка вертикальной пульсационной составляющей скорости совпадает с дифференциальной связью, которая выделяет автомодельное решение.

Для численного решения двумерной стационарной задачи тепловой конвекции идеальной жидкости выполнена модификация коллокационно-сеточного метода решения уравнений Навье-Стокса в естественных переменных. Компоненты вектора скорости приближаются линейной комбинацией векторов полиномиального соленоидального базиса, давление – в виде линейной функции, температура – в виде квадратичного многочлена. Триангуляция области проводится треугольными конечными элементами с использованием адаптивной сетки. Основы метода разработаны А.Г. Слепцовым.

Построена нормальная форма Пуанкаре для уравнений в частных производных с периодическими коэффициентами и резонансным нелинейным членом. В качестве примера рассмотрено нелинейное уравнение Шредингера с периодическими временными коэффициентами.

Пинчуков В.И. Нелинейные сеточные фильтры и их использование в схемах высоких порядков для задач аэродинамики. // Математическое моделирование.–1999. Принята в печать.

Пинчуков В.И. Гиперзвуковые вязкие течения с индуцированной отрывной зоной возле тел вращения. // Теплофизика и аэромеханика. -1999. том 6. N 3. С. 369-377.

Пинчуков В.И. ENO-модификация нелокального кубического сплайна на равномерной сетке. // Вычислительные технологии. Принята в печать.

Пинчуков В.И. Нелокальный кубический сплайн, сохраняющий направление роста интерполируемых функций. // "ЖВМиМФ".Принята в печать.

Barakhnin V.B., Borodkin N.V., Karamyshev V.B. TVD scheme on a nonstationary adaptive grid // Russian Journal of Numerical Analysis and Mathematical Modelling. – 1999. – Vol. 14. – N 4. – P. 298-309.

Paasonen V.I. Boundary conditions of high-order accuracy at the poles of сurvilinear coordinate systems // Russian Journal of Numerical Analysis and Mathematical Modelling. – 1999. – Vol. 14. – N 4. – P. 369-382.

Голушко С.К., Горшков В.В., Юрченко А.В. Анализ поведения армированного сосуда в геометрически нелинейной постановке // Динамика сплошной среды. – Выпуск 114. – 1999. – С. 155-160.

Войтович Т.В., Качанов С.М., Чубаров Л.Б., Шурина Э.П. Алгоритмы типа МКО/МКЭ для моделирования катастрофических волн в океане // Современные методы математического моделирования природных и антропогенных катастроф, V научная конференция. Тезисы докладов. – Красноярск, ИВМ СО РАН, 1999. – С. 89-91.

Lisseikina T.V., Califano F., Vshivkov V.A., Pegoraro F., Bulanov S.V. Small-scale electron density and magnetic-field structures in the wake of an ultraintense laser pulse // Physical Review. E. – 1999. – V. 60.–No. 5.– P. 5991-5997.

Вшивков В.А., Романов Д.В., Снытников В.Н. Проблема саморазогрева модельной плазмы в методе частиц // Вычислительные технологии -1999. – т.4.– N 3.– с. 62-72.

Дудникова Г.И., Романов Д.В., Федорук М.П. Об алгоритмах метода частиц на неструктурированных сетках // ЖВМиМФ. Принята в печать.

Алексеенко С.В., Дудникова Г.И., Романов В.А., Романов Д.В., Романов К.В. Разогрев солнечной атмосферы акустическими волнами // Russian Journal of Engeneering Thermophysics. Принята в печать.

Grigoryev Yu.N., Meleshko S.V., Sattayatham P. Classificatiion of the Invariant Solutions of the Boltzmann Equation // J. Physics A: mathematical and General, -1999. -Vol.32. -L337-L343.

Grigoryev Yu.N., Meleshko S.V. Classificatiion of the Invariant Solutions of the Full Boltzmann Equation // Abstr. Invited Papers. WASCOM. 10 Int. Conf. on waves and stability in cont. media. (June 7-12, 1999, Vulcano, Italy) -1999. -P.17.

Григорьев Ю.Н., Мелешко С.В. Классификация инвариантных решений полного уравнения Больцмана кинетической теории газа // Тезисы докладов международной конференции Математические модели и методы их исследования (18-24 августа 1999г., Красноярск, Россия) -1999. -Красноярск: КГУ. -С.80.

Grigoryev Yu.N., Meleshko S.V. Classificatiion of the Invariant Solutions of the Full Boltzmann Equation // Направлено в WASCOM Proceedings of 10 Int. Conf.on waves and stability in cont. media. (June 7-12, 1999, Vulcano, Italy).

Shokin Yu.I., Grigoryev Yu.N., Gorobchuk A.G. Advanced optimization of etching processes in plasma-chemical reactors // Book of abstracts of 8th International symposium on computational fluid dynamics (September 5th-10th, 1999, Bremen, Germany) -1999. -PP.106-107.

Shokin Yu.I., Grigoryev Yu.N., Gorobchuk A.G. Advanced optimization of etching processes in radial flow plasma-chemical reactor // Направлено в Proceedings of 8th International symposium on computational fluid dynamics. – 1999, Universitat Bremen, Germany, 7p.

Grigoryev Yn.N., Gorobchuk A.G. Pecularities of Si Films Etching in CF4 Parent Gas // Направлено в Proceedings of 22 International conference on microelectronics. ("MIEL-99", Yugoslavia). – 1999. – V. 1. – P. 289-292.

Григорьев Ю.Н., Горобчук А.Г. Совершенствование кинетической модели плазмохимического реактора // Тезисы докладов V научной конференции Современные методы математического моделирования природных и антропогенных катастроф (17-23 августа 1999г., Красноярск, Россия) -1999. -Красноярск: ИВМ СО РАН. -С.55-57.

Григорьев Ю.Н., Горобчук А.Г. Исследование тепломассообмена в радиальном плазмохимическом реакторе // Тезисы докладов международной конференции Математические модели и методы их исследования (18-24 августа 1999г., Красноярск, Россия) -1999. -Красноярск: КГУ. -С.79-80.

Горобчук А.Г. Особенности тепломассообмена в радиальном плазмохимическом реакторе // Тезисы докладов зимней школы-семинара молодых ученых Сопряженные задачи механики и экологии (19-21 февраля 1999г., Томск, Россия) -1999. -Томск: ТГУ. -С.26.

Grebenev V. N., Ilyushin B. B. On a class of self-similar solutions of a third-order model for the shearless turbulence mixing layer. // International Conference on Differential Equations. Abstracts. – Berlin. August 1-7. – 1999. – P. 177-178.

Medvedev S. B., Turitsyn S. K. Hamiltonian averaging and integrability in nonlinear systems with periodically varying dispersion // Письма в ЖЭТФ. – 1999. – Т.69. – Вып. 7. – С. 465-470.

Medvedev S. B. The slow manifold for the shallow water equations on the f plane. // Journal of Atmospheric Sciences. -1999. – V.56. – N 8. – P.1050-1054.

Medvedev S. B. Poincare normal forms for partial differential equations. // Proceedings Royal Society of London. Mathematical, Physical and Engineering Sciences. – 1999. – V.455. -N. 1991. – P.4063-4077.

Далее