


| § 1.7. Устойчивость разностных схем | 
|
Всякий раз как появляется дело, достойное, чтобы им заняться, имеет смысл поручить его человеку, способному с ним справиться.
Следствие 7 из принципа Питера
В отличие от схем
1.7.1. Пример.
Рассмотрим явный линейный двухшаговый метод
| xi – 3xi–1 + 2xi–2 = τ[f(ti–1, xi–1) – 2f(ti–2, xi–2)]. | (1) |
в применении к задаче Коши
| x′ = 2t, x(0) = 0. |
Очевидно ее решением является функция
Задача 1.7.1. С помощью теоремы 1.6.9 покажите, что схема (1) является схемой первого порядка аппроксимации.
Начальный запуск схемы определим, положив
| x0 = 0, x1 = τ2 |
(таким образом, начальные данные совпадают с точным решением). Тогда, как нетрудно видеть, соответствующее сеточное решение задается формулой
| (φτ)i = (2i + i2 – i –1)τ2 при i ≥ 2. | (2) |
Задача 1.7.2. Проверьте.
Заметим теперь, что при достаточно малом τ
|
|
|
Таким образом, схема (1) хотя и является аппроксимирующей, не является сходящейся. Дело здесь, разумеется, в ее неустойчивости. Попробуем понять это явление подробнее. Ответственным за несходимость решения (2) к точному решению является первое слагаемое. А источник его появления таков. Решение уравнения (1) по аналогии с линейным обыкновенным
дифференциальным уравнением (а также с системой линейных алгебраических уравнений, каковой она собственно и является) можно искать в виде "общее решение
линейного однородного уравнения + частное решение неоднородного", а первое из них в виде
| ζ i – 3ζ i–1 + 2ζ i–2 ≡ 0, |
| ζ2 – 3ζ+ 2 = 0. | (3) |
Таким образом, сеточная функция
1.7.2. Устойчивость. Наводящие соображения.
Рассмотрим линейный p-шаговый метод
| (4) |
Можно надеяться, поскольку нас интересует поведение решений при
| (5) |
получающаяся из (4) при
|
получим, что сеточная функция
|
Этот полином называется производящим полиномом метода (4). Более того, если
Задача 1.7.3. Докажите!
Очевидно, что
|
Отметим здесь же, что в силу теоремы 1.6.9 (см. условие (1.6.9)), если метод (4) является аппроксимирующим, то его производящий полином с необходимостью имеет единичный корень: |
1.7.3. Теорема об устойчивости линейных многошаговых методов.
Для того чтобы схема (4) была устойчивой, необходимо и достаточно, чтобы соответствующая однородная схема (5) удовлетворяла корневому условию.
Д о к а з а т е л ь с т в о необходимости нами, по существу, уже проведено. В самом деле, применение метода (4) к дифференциальному уравнению
Доказательство достаточности сложнее, и мы его опускаем.
Задача 1.7.4. Восстановите детали доказательства.
Задача 1.7.5. Рассмотрите случай кратного равного по модулю единице корня.
Производящий полином p-шаговых методов Адамса (как явных, так и неявных) имеет вид
1.7.4. Сходимость линейных многошаговых методов.
В силу теоремы 1.6.9 для того, чтобы линейный p-шаговый метод (4) обладал k-м порядком аппроксимации, нужно удовлетворить
Теорема Далквиста. Пусть k — порядок сходимости линейного p-шагового метода. Тогда
Эта теорема (доказательство которой мы опускаем) задает ограничение на порядок сходимости многошаговых методов. Линейные устойчивые p-шаговые методы (p+2)-го порядка аппроксимации (и, следовательно, сходимости) называются оптимальными.
1.7.5. Абсолютная устойчивость.
Обсуждавшееся выше понятие устойчивости гарантирует, что устойчивый метод хорошо работает лишь при
| x′ = λx | (6) |
с комплексным параметром λ. Мотивировка
выбора уравнения (6) в качестве модельного такова. Во-первых,
его предельная простота. Во-вторых, это уравнение "представляет" локальное поведение решение общего дифференциального уравнения (E) в следующем смысле. Решения уравнения (E) локально (в окрестности любой точки
| x′ = fx(t0, x0)x | (7) |
в окрестности нуля. В случае, когда жордановы клетки линейного оператора
Будем говорить, что метод (4) абсолютно устойчив при данном τ и данном λ ∈ C, если его глобальная погрешность
En(τ) при применении его к уравнению
(6) с данным λ при
1.7.6. Область абсолютной устойчивости.
Применение метода (4) к уравнению (6) приводит к разностной схеме
|
| (8) |
Соответствующее возмущенное уравнение имеет вид
| (9) |
Как и в п. 1.7.2, общее решение неоднородного уравнения (9) складывается из общего решения однородного уравнения (8) и частного решения неоднородного уравнения (9). Частное решение можно считать малым. Поэтому поведение (9) определяется поведением решений однородного уравнения (8). Так же, как и выше, тривиально показывается, что функция
|
называемого обычно полиномом устойчивости метода (4). Таким образом, если корни полинома лежат в единичном круге, то у уравнения (7) нет растущих решений (предоставляем читателю возможность произнести все нужные слова, относящиеся к корням, лежащим на границе круга).
По существу, мы показали, что если при данном τ и
1.7.7. Пример: область устойчивости неявного метода Эйлера.
Полином устойчивости неявного метода Эйлера, очевидно, имеет вид
| πz(ζ) = (1 – z)ζ– 1. |
Его единственный корень —
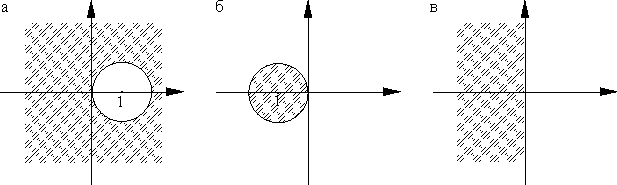
Задача 1.7.6. Докажите, что для явного метода Эйлера
1.7.8. Зачем нужно знать область устойчивости метода?
Тривиальный пример применения неявного метода Эйлера для нахождения нулевого решения задачи Коши
| x′ = x, x(0) = 0 |
показывает, что погрешность ε0 в определении начального условия распространяется по закону
| εi = (1 – τ)–iε0. |
Очевидно, если шаг
Поэтому для контроля шага (особенно при применении одношаговых методов к системам малой размерности) иногда поступают так. Через некоторое число шагов находят матрицу Якоби fx и все ее собственные значения, а затем корректируют шаг так, чтобы произведение шага на каждое собственное значение лежало в области устойчивости используемого метода. Эта процедура достаточно дорогостояща. Поэтому в случае больших размерностей ее обычно не применяют.
Кроме того, форма и размеры области абсолютной устойчивости важны при сравнении различных методов.
Несколько слов о нахождении области абсолютной устойчивости метода. Для простых случаев область может быть указана аналитически. В более сложных ситуациях применяют следующее рассуждение. Если точка z лежит на границе ∂S области S, то при этом z полином устойчивости πzимеет корень ζ, равный по модулю единице:
| πz(eiα) = 0. | (10) |
Решим при каждом
File based on translation from
TEX by TTH,
version 3.05.
Created On 29 May 2002, 8: 37.