0.1.3. Базисы и кобазисы

Для любого базиса {e_i} кобазис {eⁱ} однозначно определяется соотношениями

eiej = dji   (i, j = 1, ..., m),

(2)

где d_jⁱ — так называемый d-символ Кронекера:

dji =  м н о 1, если i = j, 0, если i № j.

Геометрически соотношение (2) означает, что вектор eⁱ кобазиса ортогонален векторам e₁, ..., e_i–1, e_i+1, ..., e_m базиса (см. рис. 2.1). Базис, совпадающий со своим кобазисом, называется ортонормальным: e_ie_j = d_jⁱ. В частности, все векторы ортонормального базиса имеют единичную длину.

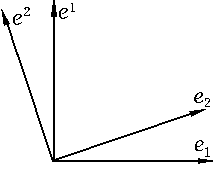
Рис. 0.1.